图灵的基本思想

图灵的基本思想是用机器来模拟人们用纸笔进行数算的过程，他把这样的过程看作下列两种简单的动作：

在纸上写上或擦除某个符号；

把注意力从纸的一个位置移动到另一个位置；

而在每个阶段，人要决定下一步的动作，依赖于（a）此人当前所关注的纸上某个位置的符号和（b）此人当前思维的状态。

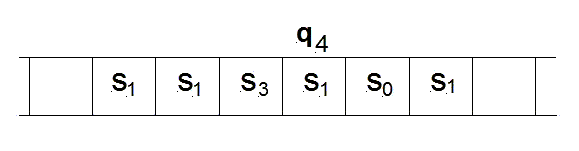
  在某些模型中，纸带移动，而未用到的纸带真正是“空白”的。要进行的指令（ q4 ）展示在扫描到方格之上（由Kleene（1952）p.375绘制）。

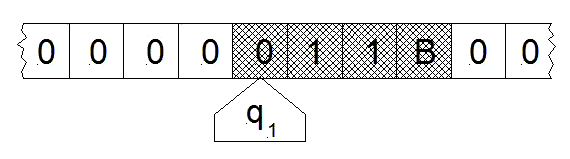
  在某些模型中，读写头沿着固定的纸带移动。要进行的指令（ q1 ）展示在读写头内。在这种模型中“空白”的纸带是全部为0的。有阴影的方格，包括读写头扫描到的空白，标记了1,1,B的那些方格，和读写头符号，构成了系统状态。（由Minsky（1967）p.121绘制）

为了模拟人的这种运算过程，图灵构造出一台假想的机器，该机器由以下几个部分组成：

一条无限长的纸带 TAPE 。纸带被划分为一个接一个的小格子，每个格子上包含一个来自有限字母表的符号，字母表中有一个特殊的符号 ◻ ◻ --> {\displaystyle \square } 表示空白。纸带上的格子从左到右依次被编号为0, 1, 2, ...，纸带的右端可以无限伸展。

一个读写头 HEAD 。该读写头可以在纸带上左右移动，它能读出当前所指的格子上的符号，并能改变当前格子上的符号。

一套控制规则 TABLE 。它根据当前机器所处的状态以及当前读写头所指的格子上的符号来确定读写头下一步的动作，并改变状态寄存器的值，令机器进入一个新的状态。

一个 状态寄存器 。它用来保存图灵机当前所处的状态。图灵机的所有可能状态的数目是有限的，并且有一个特殊的状态，称为 停机状态 。参见停机问题。

注意这个机器的每一部分都是有限的，但它有一个潜在的无限长的纸带，因此这种机器只是一个理想的设备。图灵认为这样的一台机器就能模拟人类所能进行的任何计算过程。

图灵机的正式定义

一台 图灵机 是一个七元有序组 ( Q , Σ Σ --> , Γ Γ --> , δ δ --> , q 0 , q a c c e p t , q r e j e c t ) {\displaystyle (Q,\Sigma ,\Gamma ,\delta ,q_{0},q_{accept},q_{reject})} ，其中 Q , Σ Σ --> , Γ Γ --> {\displaystyle Q,\Sigm有限集合Gamma } 都是有限集合，且满足

Q {\displaystyle Q} 是非空有穷状态集合；

Σ Σ --> {\displaystyle \Sigma } 是非空有穷输入字母表，其中不包含特殊的空白符 ◻ ◻ --> {\displaystyle \square } ；

Γ Γ --> {\displaystyle \Gamma } 是非空有穷带字母表且 Σ Σ --> ⊂ ⊂ --> Γ Γ --> {\displaystyle \Sigma \subset \Gamma } ；

◻ ◻ --> ∈ ∈ --> Γ Γ --> − − --> Σ Σ --> {\displaystyle \square \in \Gamma -\Sigma } 为 空白符 ，也是唯一允许出现无限次的字符；

δ δ --> : Q × × --> Γ Γ --> → → --> Q × × --> Γ Γ --> × × --> { L , R , − − --> } {\displaystyle \delta :Q\times \Gamma \to Q\times \Gamma \times \{L,R,-\}} 是转移函数，其中 L , R {\displaystyle L,R} 表示读写头是向左移还是向右移, - 表示不移动；

q 0 ∈ ∈ --> Q {\displaystyle q_{0}\in Q} 是起始状态；

q a c c e p t ∈ ∈ --> Q {\displaystyle q_{accept}\in Q} 是接受状态。 q r e j e c t ∈ ∈ --> Q {\displaystyle q_{reject}\in Q} 是拒绝状态，且 q r e j e c t ≠ ≠ --> q a c c e p t {\displaystyle q_{reject}\neq q_{accept}} 。

图灵机 M = ( Q , Σ Σ --> , Γ Γ --> , δ δ --> , q 0 , q a c c e p t , q r e j e c t ) {\displaystyle M=(Q,\Sigma ,\Gamma ,\delta ,q_{0},q_{accept},q_{reject})} 将以如下方式运作：

开始的时候将输入符号串 ω ω --> = ω ω --> 0 ω ω --> 1 … … --> ω ω --> n − − --> 1 ∈ ∈ --> Σ Σ --> ∗ ∗ --> {\displaystyle \omega =\omega _{0}\omega _{1}\ldots \omega _{n-1}\in \Sigma ^{*}} 从左到右依此填在纸带的第 0 , 1 , … … --> , n − − --> 1 {\displaystyle 0,1,\ldots ,n-1} 号格子上，其他格子保持空白（即填以空白符 ◻ ◻ --> {\displaystyle \square } )。 M {\displaystyle M} 的读写头指向第0号格子， M {\displaystyle M} 处于状态 q 0 {\displaystyle q_{0}} 。机器开始运行后，按照转移函数 δ δ --> {\displaystyle \delta } 所描述的规则进行计算。例如，若当前机器的状态为 q {\displaystyle q} ，读写头所指的格子中的符号为 x {\displaystyle x} ，设 δ δ --> ( q , x ) = ( q ′ , x ′ , L ) {\displaystyle \delta (q,x)=(q",x",L)} ，则机器进入新状态 q ′ {\displaystyle q"} ，将读写头所指的格子中的符号改为 x ′ {\displaystyle x"} ，然后将读写头向左移动一个格子。若在某一时刻，读写头所指的是第0号格子，但根据转移函数它下一步将继续向左移，这时它停在原地不动。换句话说，读写头始终不移出纸带的左边界。若在某个时刻 M {\displaystyle M} 根据转移函数进入了状态 q a c c e p t {\displaystyle q_{accept}} ，则它立刻停机并接受输入的字符串； 若在某个时刻 M {\displaystyle M} 根据转移函数进入了状态 q r e j e c t {\displaystyle q_{reject}} ，则它立刻停机并拒绝输入的字符串。

注意，转移函数 δ δ --> {\displaystyle \delta } 是一个部分函数，换句话说对于某些 q {\displaystyle q} , x {\displaystyle x} ， δ δ --> ( q , x ) {\displaystyle \delta (q,x)} 可能没有定义，如果在运行中遇到下一个操作没有定义的情况，机器将立刻停机。

图灵机的基本术语

设 M = ( Q , Σ Σ --> , Γ Γ --> , δ δ --> , q 0 , q a c c e p t , q r e j e c t ) {\displaystyle M=(Q,\Sigma ,\Gamma ,\delta ,q_{0},q_{accept},q_{reject})} 是一台图灵机，

M {\displaystyle M} 的 带描述（tape description） 是一个函数 F : N → → --> Γ Γ --> {\displaystyle F:\mathbb {N} \to \Gamma } ，其中 F ( i ) {\displaystyle F(i)} 表示 M {\displaystyle M} 的带上第 i {\displaystyle i} 个格子中的符号；

M {\displaystyle M} 的 格局（configuration） 是一个三元组 ( F , q , e ) {\displaystyle (F,q,e)} ，其中 F : N → → --> Γ Γ --> {\displaystyle F:\mathbb {N} \to \Gamma } 是当前的带描述， q ∈ ∈ --> Q {\displaystyle q\in Q} 是当前的状态， e ∈ ∈ --> N {\displaystyle e\in \mathbb {N} } 是当前读写头所处的位置；

设 C 1 = ( F 1 , q 1 , e 1 ) {\displaystyle C_{1}=(F_{1},q_{1},e_{1})} , C 2 = ( F 2 , q 2 , e 2 ) {\displaystyle C_{2}=(F_{2},q_{2},e_{2})} 是 M {\displaystyle M} 的格局，设 δ δ --> ( q 1 , F 1 ( e 1 ) ) = ( q , x , d ) {\displaystyle \delta (q_{1},F_{1}(e_{1}))=(q,x,d)} ，若满足 q 2 = q {\displaystyle q_{2}=q} ， e 2 = { e 1 − − --> 1 d = L e 1 + 1 d = R {\displaystyle e_{2}={\begin{cases}e_{1}-1&d=L\\e_{1}+1&d=R\end{cases}}} 以及 F 2 ( i ) = { F 1 ( i ) i ≠ ≠ --> e 1 x i = e 1 {\displaystyle F_{2}(i)={\begin{cases}F_{1}(i)&i\neq e_{1}\\x&i=e_{1}\end{cases}}} 则称 M {\displaystyle M} 从格局 C 1 {\displaystyle C_{1}} 产生 格局 C 2 {\displaystyle C_{2}} ，记作 C 1 → → --> M C 2 {\displaystyle C_{1}\to _{M}C_{2}} 。

设 C = ( F , q , e ) {\displaystyle C=(F,q,e)} 为 M {\displaystyle M} 的格局，若 q = q a c c e p t {\displaystyle q=q_{accept}} 则称 C {\displaystyle C} 为 接受格局 ；若 q = q r e j e c t {\displaystyle q=q_{reject}} 则称 C {\displaystyle C} 为 拒绝格局 ；接受格局和拒绝格局统称为 停机格局 。

设 M {\displaystyle M} 是一台图灵机，将字符串 ω ω --> = ω ω --> 0 ω ω --> 1 … … --> ω ω --> n − − --> 1 {\displaystyle \omega =\omega _{0}\omega _{1}\ldots \omega _{n-1}} 作为其输入，若存在格局序列 C 1 , C 2 , … … --> , C k {\displaystyle C_{1},C_{2},\ldots ,C_{k}} ，使得

C 1 {\displaystyle C_{1}} 是 M {\displaystyle M} 在输入 ω ω --> {\displaystyle \omega } 上的起始格局，即 C 1 = ( F , q 0 , 0 ) {\displaystyle C_{1}=(F,q_{0},0)} ，其中 F 1 ( i ) = { ω ω --> i 0 ≤ ≤ --> i ≤ ≤ --> n − − --> 1 ◻ ◻ --> otherwise {\displaystyle F_{1}(i)={\begin{cases}\omega _{i}&0\leq i\leq n-1\\\square &{\mbox{otherwise}}\end{cases}}}

C i → → --> M C i + 1 {\displaystyle C_{i}\to _{M}C_{i+1}} ，其中 i = 1 , 2 , … … --> , k − − --> 1 {\displaystyle i=1,2,\ldots ,k-1} ；

C k {\displaystyle C_{k}} 是接受格局。

则称 M {\displaystyle M} 接受 字符串 ω ω --> {\displaystyle \omega } ，且 C 1 , C 2 , … … --> , C k {\displaystyle C_{1},C_{2},\ldots ,C_{k}} 称为图灵机 M {\displaystyle M} 在输入 ω ω --> {\displaystyle \omega } 上的 接受计算历史 。同理，若 C k {\displaystyle C_{k}} 是拒绝格局，则称 M {\displaystyle M} 拒绝 ω ω --> {\displaystyle \omega } ，且 C 1 , C 2 , … … --> , C k {\displaystyle C_{1},C_{2},\ldots ,C_{k}} 称为图灵机 M {\displaystyle M} 在输入 ω ω --> {\displaystyle \omega } 上的 拒绝计算历史 。 M {\displaystyle M} 所接受的所有字符串的集合称为 M {\displaystyle M} 的 语言 ，记作 L ( M ) {\displaystyle L(M)} 。

图灵机的例子

设 M = ( { 0 , 1 , 10 , 11 } , { 0 , 1 } , { 0 , 1 , ◻ ◻ --> } , δ δ --> , 0 , , ) {\displaystyle M=(\{0,1,10,11\},\{0,1\},\{0,1,\square \},\delta ,0,,)} 和 δ δ --> : { 0 , 1 , 10 , 11 } × × --> { 0 , 1 } → → --> { 0 , 1 , 10 , 11 } × × --> { 0 , 1 } × × --> { R , L , E , S } {\displaystyle \delta :\{0,1,10,11\}\times \{0,1\}\to \{0,1,10,11\}\times \{0,1\}\times \{R,L,E,S\}} . 比如做一个以1的个数表示数值的加法运算，在磁带上的数据是0000001110110000，就是3+2的意思。程序 δ δ --> {\displaystyle \delta } 如下：

第一行程序0,0->0,0R意思就是如果机器读到0，就将其变成0，状态变为0，读写头向右移动一格. R就是向右移动一格，L就是向左移一格，E是错误，S是停机. xx,y -> aa,b中xx是当前状态, y是当前格子的值, aa是程序下一步的状态, b是当前格的修改值。

虽然这里给出与上面不同形式的定义，但两者是等价的，这里的定义能完成的工作并不比上面的定义多。

通用图灵机

对于任意一个图灵机，因为它的描述是有限的，因此我们总可以用某种方式将其编码为字符串。我们用 〈 〈 --> M 〉 〉 --> {\displaystyle \langle M\rangle } 表示图灵机 M {\displaystyle M} 的编码。

我们可以构造出一个特殊的图灵机，它接受任意一个图灵机 M {\displaystyle M} 的编码 〈 〈 --> M 〉 〉 --> {\displaystyle \langle M\rangle } ，然后模拟 M {\displaystyle M} 的运作，这样的图灵机称为 通用图灵机 （Universal Turing Machine）。现代电子计算机其实就是这样一种通用图灵机，它能接受一段描述其他图灵机的程序，并运行程序实现该程序所描述的算法。

图灵机的变体

图灵机有很多变种，但可以证明这些变种的计算能力都是等价的，即它们识别同样的语言类。证明两个计算模型 A {\displaystyle A} 和 B {\displaystyle B} 的计算能力等价的基本思想是：用 A {\displaystyle A} 和 B {\displaystyle B} 相互模拟，若 A {\displaystyle A} 可模拟 B {\displaystyle B} 且 B {\displaystyle B} 可模拟 A {\displaystyle A} ，显然他们的计算能力等价。注意这里我们暂时不考虑计算的效率，只考虑计算的理论上“可行性”。

首先我们可以发现，改变图灵机的带字母表并不会改变其计算能力。例如我们可以限制图灵机的带字母表为 { 0 , 1 } {\displaystyle \{0,1\}} ，这并不会改变图灵机的计算能力，因为我们显然可以用带字母表为 { 0 , 1 } {\displaystyle \{0,1\}} 的图灵机模拟带字母表为任意有限集合 Γ Γ --> {\displaystyle \Gamma } 的图灵机。

另一个要注意的是，如果我们允许图灵机的纸带两端都可以无限伸展，这并不能增加图灵机的计算能力，因为我们显然可以用只有纸带一端能无限伸展的图灵机来模拟这种纸带两端都可以无限伸展的图灵机。

如果我们允许图灵机的读写头在某一步保持原地不动，那也不会增加其计算能力，因为我们可以用向左移动一次再向右移动一次来代替在原地不动。

其它的常见图灵机变种包括：

多带图灵机

非确定型图灵机

交替式图灵机

枚举器

图灵可计算性

图灵可识别语言

图灵可判定语言

递归可枚举语言

可计算函数

递归函数

停机问题

可判定性

不可判定性

不可解度

其它等价的计算模型

除了图灵机以外，人们还发明了很多其它的计算模型。包括：

寄存器机

递归函数

λ演算

生命游戏

马尔可夫算法

然而这些模型无一例外地都和图灵机的计算能力等价，因此邱奇，图灵和哥德尔提出了著名的邱奇-图灵论题：一切 直觉上能计算 的函数都可用图灵机计算，反之亦然。

参考文献

Turing, A.,On Computable Numbers, With an Application to the Entscheidungsproblem, Proceedings of the London Mathematical Society, Series 2, Volume 42, 1936; reprinted in M. David（ed.）, The Undecidable, Hewlett, NY: Raven Press, 1965;

Michael Sipser, Introduction to the Theory of Computation, PWS Publishing, 1997. ISBN 0-534-94728-X

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。