双射-族谱新闻-族谱网

双射

2020-10-16

出处：族谱网

作者：阿族小谱

浏览:390次

转发:0次

评论:0

复合函数与反函数一函数f为双射的当且仅当其逆关系f也是个函数。在这情况，f也会是双射函数。两个双射函数f:{displaystyle;:;}X↔↔-->{displaystyle{}l

复合函数与反函数

一函数 f 为双射的当且仅当其逆关系 f 也是个函数。在这情况， f 也会是双射函数。

两个双射函数 f : {\displaystyle \;:\;} X ↔ ↔ --> {\displaystyle {}\leftrightarrow {}} Y 及 g : {\displaystyle \;:\;} Y ↔ ↔ --> {\displaystyle {}\leftrightarrow {}} Z 的复合函数 g o f 亦为双射函数。其反函数为( g o f ) = ( f ) o ( g )。

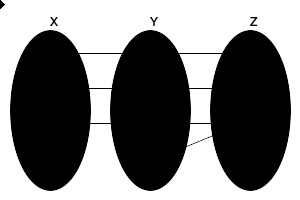
一个复合所得的双射，左侧为单射，右侧为满射。

另一方面，若 g o f 为双射的，可知 f 是单射的且 g 是满射的，但也仅限于此。

一由 X 至 Y 的关系 f 为双射函数当且仅当存在另一由 Y 至 X 的关系 g ，使得 g o f 为 X 上的恒等函数，且 f o g 为 Y 上的恒等函数。必然地，此两个集合会有相同的势。

双射与势

若 X 和 Y 为有限集合，则其存在一两集合的双射函数当且仅当两个集合有相同的元素个数。确实，在公理集合论里，这正是“相同元素个数”的定义，且广义化至无限集合，并导致了基数的概念，用以分辨无限集合的不同大小。

例子与反例

对任一集合 X ，其恒等函数为双射函数。

函数 f : R → → --> {\displaystyle \rightarrow } R ，，其形式为 f ( x ) = 2 x + 1，是双射的，因为对任一 y ，存在一唯一 x = ( y − 1)/2使得 f ( x ) = y 。

指数函数 g : R → → --> {\displaystyle \rightarrow } R ，其形式为 g(x) = e ，不是双射的：因为不存在一 R 内的 x 使得 g ( x ) = −1，故 g 非为双射。但若其陪域改成正实数 R = (0,+∞)，则 g 便是双射的了；其反自然对数然对数函数 ln。

函数 h : R → → --> {\displaystyle \rightarrow } [0,+∞)，其形式为 h ( x ) = x ²，不是双射的：因为 h (−1) = h (1) = 1，故 h 非为双射。但如果把定义域也改成[0,+∞)，则 h 便是双射的了；其反函数为正平方根函数。

R → → --> R : x ↦ ↦ --> ( x − − --> 1 ) x ( x + 1 ) = x 3 − − --> x {\displaystyle \mathbf {R} \to \mathbf {R} :x\mapsto (x-1)x(x+1)=x^{3}-x} 不是双射函数，因为−1, 0和1都在其定义域里且都映射至0。

R → → --> [ − − --> 1 , 1 ] : x ↦ ↦ --> sin ⁡ ⁡ --> ( x ) {\displaystyle \mathbf {R} \to [-1,1]:x\mapsto \sin(x)} 不是双射函数，因为π/3和2π/3都在其定义域里且都映射至 3 / 2 {\displaystyle {\sqrt {3}}/2} 。

性质

一由实数 R 至 R 的函数 f 是双射的，当且仅当其图像和任一水平线相交且只相交于一点。

设 X 为一集合，则由 X 至其本身的双射函数，加上其复合函数( )的运算，会形成一个群，即为 X 的对称群，其标记为S( X )、 S X 或 X !。

取一定义域的子集 A 及一陪域的子集 B ，则

若 X 和 Y 为具相同势的有限集合，且 f : X → Y ，则下列三种说法是等价的：

双射与范畴论

形式上，双射函数恰好是集合范畴内的同构。

另见

单射

同构

置换

对称群