



坐标系
数轴
数轴是最简单的坐标系,用一个实数标示一个点在线上的位置。数轴中会有一个原点 O ,以及单位长度及其方向。点 P 的坐标为从 O 到 P 的有号距离,坐标是正值或负值则依 P 点在原点的哪一侧来决定。数轴上每一个点都有唯一的坐标,每一个实数也都可以在数轴上找到唯一的对应点
笛卡儿坐标系
笛卡儿坐标系也称为直角坐标系,是最常用到的一种坐标系。是法国数学家勒内·笛卡尔在1637年发表的《方法论》附录中提到的 。 在平面上,选定二条互相垂直的线为坐标轴,任一点距坐标轴的有号距离为另一轴的坐标,这就是二维的笛卡儿坐标系,一般会选一条指向右方水平线称为x轴,再选一条指向上方的垂直线称为y轴,此两坐标轴设定方式称为“右手坐标系”。
若在三维系统中,选定三条互相垂直的平面,任一点距平面的有号距离为坐标,二平面的交线为坐标轴,即可产生三维的笛卡儿坐标系。一般会选择x轴及y轴是水平的,z轴垂直往上,且三轴维持右手定则,若先将右手的手掌与手指伸直。然后,将中指指向往手掌的掌面 半空间,与食指呈直角关系。再将大拇指往上指去,与中指,食指都呈直角关系。则大拇指,食指,与中指分别表示了右手坐标系的 x-轴,y-轴,与 z-轴。
此概念可以延伸,在 n 维的欧几里得空间中建立 n 维的笛卡儿坐标系。
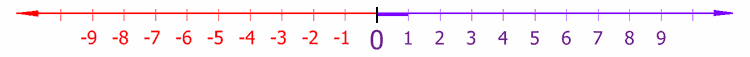
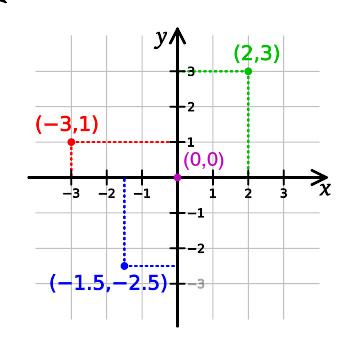
平面的笛卡儿坐标系
极坐标系
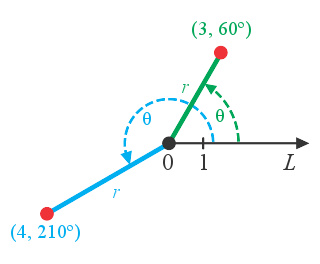
平面上的极坐标系
极坐标系也是一种常用的平面坐标系统。实际上应用“极坐标”这个术语的是由格雷古廖·丰塔纳( Gregorio Fontana )开始的,是由乔治·皮科克( George Peacock )在1816年翻译席维斯·拉克鲁克斯( Sylvestre François Lacroix )的《微分学与积分学》( Traité du calcul différentiel et du calcul intégral ) 一书时,被翻译为英语的。
极坐标中会定一点为极点,再将一条通过极点的射线定为极轴。若给定一角度θ,则可绘出通过极点,和极轴夹角为θ的唯一射线(角度是以从极轴,依逆时针方向旋转到射线),若再给定一实数r,可找出上述射线上,距极点距离为有号整数r的一点 。
在极坐标系中,一坐标( r , θ)只会其对应唯一的一点,但每一点均可对应许多个坐标。例如坐标( r , θ)、 ( r , θ+2π)及(− r , θ+π)都是对应同一点的不同坐标。而极点的坐标为(0, θ),θ可为任意值。
极坐标 r {\displaystyle r\,} 和 θ θ --> {\displaystyle \theta \,} 可以用下式变换为直角坐标:
从直角坐标 x {\displaystyle x\,} 和 y {\displaystyle y\,} 也可以变换为极坐标:
圆柱坐标系及球坐标系
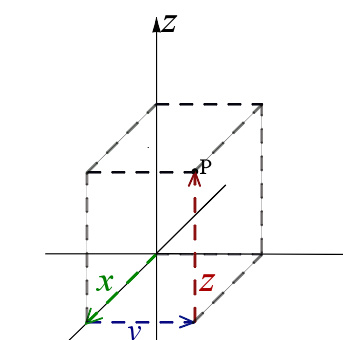
若将平面上的极坐标系扩展到立体的空间,可扩展为圆柱坐标系及球坐标系。圆柱坐标系是将极坐标系的 ( r , θ θ --> ) {\displaystyle (r,\ \theta )} 坐标变成 ( ρ ρ --> , ϕ ϕ --> ) {\displaystyle (\rho ,\ \phi )} ,再增加一个笛卡尔坐标系的z坐标。如P 点的圆柱坐标是 ( ρ ρ --> , ϕ ϕ --> , z ) {\displaystyle (\rho ,\ \phi ,\ z)} 。
ρ ρ --> {\displaystyle \rho } 是原点至P点之间的距离。
ϕ ϕ --> {\displaystyle \phi } 是线 OP 在 xy-面的投影线与正 x-轴之间的夹角。
z与直角坐标的 z {\displaystyle z} 等值。
直角坐标和圆柱坐标系的转换关系如下 :
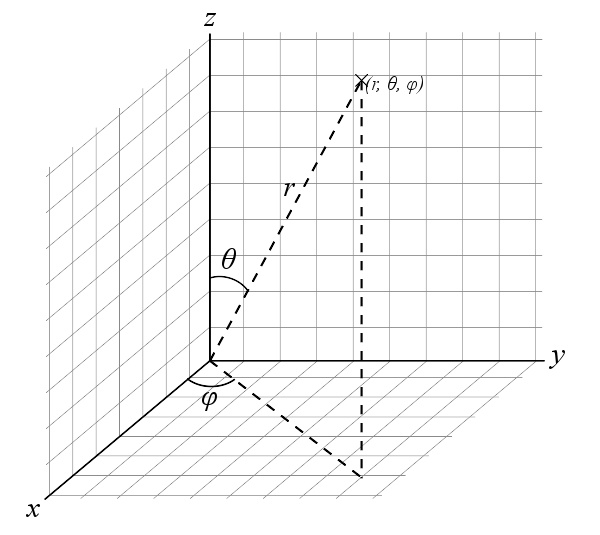
用球坐标 ( r , θ θ --> , ϕ ϕ --> ) {\displaystyle (r,\ \theta ,\ \phi )} 来表示一个点的位置
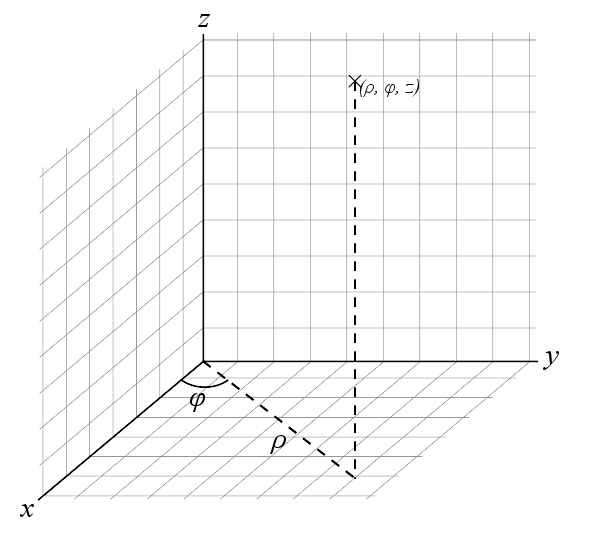
用圆柱坐标 ( ρ ρ --> , ϕ ϕ --> , z ) {\displaystyle (\rho ,\ \phi ,\ z)} 来表示一个点的位置
而球坐标系则是用一个角度 ϕ ϕ --> {\displaystyle \phi } 表示位置和xy-面的相对关系。如P 点的球坐标为 ( r , θ θ --> , ϕ ϕ --> ) {\displaystyle (r,\ \theta ,\ \phi )} 。
r {\displaystyle r} 是原点至P点在xy-面上投影点之间的距离。
ϕ ϕ --> {\displaystyle \phi } 是线 OP 在 xy-面的投影线与正 x-轴之间的夹角。
θ θ --> {\displaystyle \theta } 为原点到点 P 的连线与正 z-轴之间的天顶角。
直角坐标和球坐标系的转换关系如下 :

球坐标系下的坐标曲面
齐次坐标
在齐次坐标表示时,会增加一个额外的坐标,例如平面上的一点可以表示为( x , y , z ),其中 x / z 及 y / z 为其原来在平面上的笛卡尔坐标。其优点是可以在不使用无限大的情形下表示射影平面上的任意点。一般齐次坐标会用在坐标之间的比例比实际的数值来的重要的情形下。
其他几何形状的坐标表示
坐标系常用来描述一个点的位置,不过也可以用坐标系描述其他复杂形状的位置,例如直线、平面、圆或是球等。例如普吕克坐标就是用来描述空间中直线的位置。当有需要时,可以在坐标系的前面加上需描述的形状做为识别,例如 直线坐标 ( 英语 : line coordinates ) 就是指描述直线位置的坐标。曲线为平行坐标轴的直线。其他坐标系的坐标曲线就是一般的曲线。例如在极坐标系中,若固定 r 为定值所形成的坐标曲线是圆心在原点的圆。在欧几里得空间中笛卡尔坐标系以外的坐标系即称为 曲线坐标系 ( 英语 : Curvilinear coordinates ) 。
若在三维坐标系中一个坐标维持定值,允许其他坐标变动,所形成的曲面称为坐标曲面。例如在球坐标系,若固定 ρ 为定值所形成的坐标曲面是球心在原点的球。三维空间中二坐标曲面的交线即为坐标曲线。在更高维度的空间也可依此定义坐标超曲面 。
坐标图
坐标图(coordinate map)的概念是流形理论的核心。本质上坐标图是一个针对给定空间子集的坐标系,其中每一个点都恰有一个对应的坐标。若要精准的定义,坐标图可定义为从空间 X 的开子集到 R 的开子集的同胚。一般的坐标系不太可能针对所有空间中的点都有明确唯一的坐标。此时可以用一组坐标图形成一个适合此空间的图册。有此性质的空间称为流形,若坐标图重叠的部分符合某些特定的结构,也可以定义有特殊结构的流形。例如微分流形就是坐标图之间的转换恒为微分函数的流形。
坐标的变换
在几何学及运动学中,坐标系不但会用来描述点的直线位置,也会用来描述轴、 正切角 ( 英语 : tangential angle ) 平面或刚体的角度取向。一般会设定一固定于刚体的参考系,称为
坐标转换
坐标转换是指在描述同一个空间时,由原来的坐标系转换为另一个坐标系。
对于每一个由空间到空间本身的双射,可定义二种坐标转换:
一种是每一个点在新坐标系坐标的双射,恰为旧坐标系的坐标。
一种是每一个点在旧坐标系坐标的双射,恰为新坐标系的坐标。
例如一维的系统中,若一映射为是往右移三个单位,则第一个坐标转换会将原点从0移到3,因此每个点的坐标都少了3,第二个座标转换会将原点从0移到-3,因此每个点的坐标都多了3。
坐标之间的转换有一定的公式。例如若平面上的笛卡尔坐标( x , y )及极坐标( r , θ )原点相同,则可以用以下的公式从极坐标转换为笛卡尔坐标: x = r cos θ 及 y = r sin θ 。
坐标曲线及坐标曲面
若在二维坐标系中一个坐标维持定值,只允许一个坐标变动,所形成的曲线称为坐标曲线(或坐标线)。不过不是所有的坐标系都有坐标曲线,例如齐次坐标系中就没有坐标曲线。
在笛卡尔坐标系中,坐标附体参考系,另一个不随刚体变动的参考则为空间参考系。一般刚体的运动可以在附体参考系下的坐标来表示,再根据附体参考系相对空间参考系的位置及取向来取得刚体相对空间的运动。例如刚体的角度取向可以用一个方向矩阵来描述,矩阵的三个栏是三个点的笛卡尔坐标,这些可用来标示局部坐标系统的坐标轴方向,也可用来计算坐标轴的单位矢量。
常用的坐标系
以下是一些常用的坐标系:
三维空间中的笛卡尔坐标系(也称为直角坐标系)是定义三个互相垂直的坐标平面,一点的坐标即为点到各坐标平面的垂直距离。
曲线坐标系 ( 英语 : Curvilinear_coordinates ) 是一种广义的坐标系,此坐标系是以相交的曲线为基础。
平面上的极坐标系是以用一点相对原点的角度及距离来表示。
平面上的 对数-极坐标系 ( 英语 : Log-polar coordinates ) 是以用一点相对原点的角度及其距离的对数来表示。
三维空间中的圆柱坐标系是以一个角度、高度及一长度来表示一个点。
三维空间中的球坐标系是以二个角度及点到原点的距离来表示一个点。
普吕克坐标可以将三维空间中的直线描述为6个齐次坐标。
广义坐标是在处理拉格朗日力学时使用。
正则坐标是在处理哈密顿力学时使用。
平行坐标将n-维空间中的一点表示为和n条垂直线有交点的折线。
重心坐标一般用在 三角图 ( 英语 : Ternary plot ) 中。
可有一些描述曲线的方式和坐标系无关,这类的方式会使用 本征方程 ( 英语 : intrinsic equation ) ,其中有用到像是曲率及弧长等不随坐标系而改变的不变量。这类的本征方程包括:
惠威尔方程 ( 英语 : Whewell equation ) 和弧长和有关。
切萨罗方程 ( 英语 : Cesàro equation ) 和弧长及曲率有关。
正交坐标系列表
数学上,二个互相垂直的矢量称为正交。以下的坐标系都是正交坐标系,其坐标曲面之间的夹角为直角。
象限
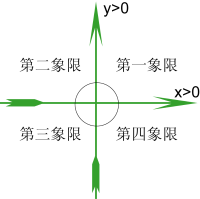
四象限图示
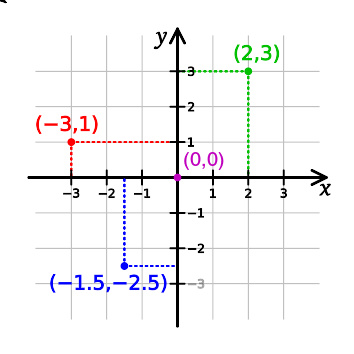
以笛卡儿平面坐标系为基准,右上为第一象限,左上为第二,左下为第三,右下就是第四象限,第一象限的x坐标和y坐标均为正值,第二象限的x坐标为负值,y坐标为正值,第三象限的x坐标和y坐标均为负值,第四象限的x坐标为正值,y坐标为负值 ,而平面坐标分六大部分,除了四个象限,还有x轴与y轴。
在笛卡儿空间坐标系中也可以依xy平面,xz平面及yz平面将不含上述平面空间分为八份,称为卦限,但一般只定义坐标均大于零的为第一卦限。
坐标中的各轴线不属于象限或卦限。
参照
字母数字网格 ( 英语 : Alpha-numeric grid )
天球坐标系统
参考系
伽利略变换
诺谟图,不同坐标系的图象表示法
经纬度
参考资料
Voitsekhovskii, M.I.; Ivanov, A.B.,Coordinates, (编) Hazewinkel, Michiel,数学百科全书, Springer, 2001, ISBN 978-1-55608-010-4
Woods, Frederick S.Higher Geometry. Ginn and Co. 1922: 1ff.
Shigeyuki Morita, Teruko Nagase, Katsumi Nomizu.Geometry of Differential Forms. AMS Bookstore. 2001: 12. ISBN 0821810456.
免责声明:以上内容版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。感谢每一位辛勤著写的作者,感谢每一位的分享。

- 有价值
- 一般般
- 没价值








推荐阅读


关于我们

APP下载


















