



锯齿波
相关条目正弦波、方波、三角波和锯齿波的波形方波三角波参考文献HughL.Montgomery;RobertC.Vaughan.MultiplicativenumbertheoryI.Classicaltheory.Cambridgetractsinadvancedmathematics97.2007:536–537.ISBN0-521-84903-9.
相关条目
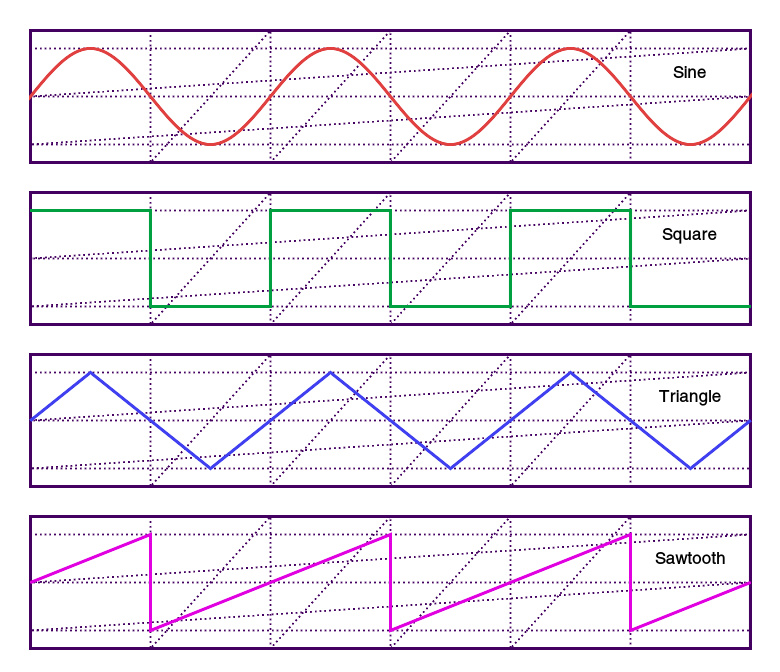
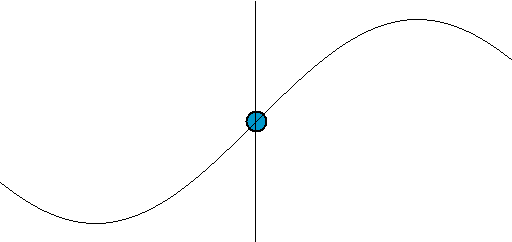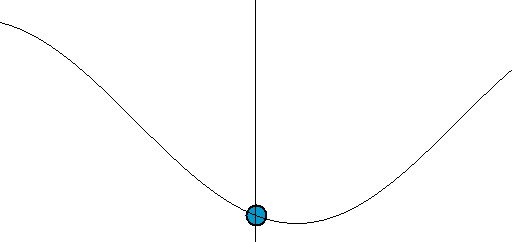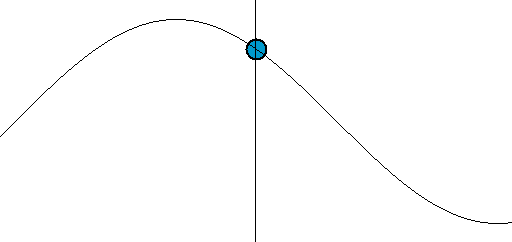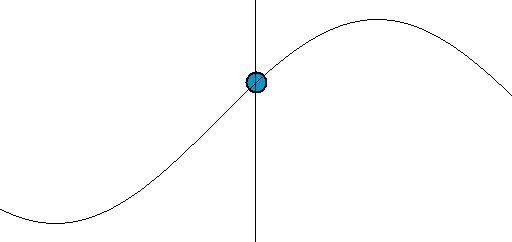
正弦波、方波、三角波和锯齿波的波形
方波
三角波
参考文献
Hugh L. Montgomery; Robert C. Vaughan. Multiplicative number theory I. Classical theory. Cambridge tracts in advanced mathematics 97. 2007: 536–537. ISBN 0-521-84903-9.
免责声明:以上内容版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。感谢每一位辛勤著写的作者,感谢每一位的分享。
——— 没有了 ———
编辑:阿族小谱

文章价值打分
- 有价值
- 一般般
- 没价值
当前文章打 0 分,共有 0 人打分
文章观点支持

0

0
文章很值,打赏犒劳一下作者~

发表评论
写好了,提交
{{item.label}}
{{commentTotal}}条评论
{{item.userName}}
发布时间:{{item.time}}
{{item.content}}
回复
举报


打赏作者
“感谢您的打赏,我会更努力的创作”
— 请选择您要打赏的金额 —
{{item.label}}


{{item.label}}

打赏成功!
“感谢您的打赏,我会更努力的创作”
返回
打赏
私信
24小时热门
推荐阅读
· 反锯齿
反锯齿技术的出现由于高分辨率下的来源信号或连续的类比信号能够存储较多的数据,但在通过取样(sampling)时将较多的数据以较少的数据点代替,部分的数据被忽略造成取样结果有损,死机器把取样后的数字信号转换为人类可辨别的类比信号时造成彼此交叠且有损,在声音中,便会出现刺耳、不和谐的音调或是噪音。同样,在3D绘图时,每个图形由像素组成,每段瞬间画面由帧组成,因为屏幕上的像素有限,如果要表现出多边形的位置时,因技术所限,使用绝对坐标定位法是无法做到的,只能使用在近似位置采样来进行相对定位。由于没有足够的采样来表现出3D世界中的所有物品的图形,所以在最后图像显示上,这些现象便会造成在物品与物品中过渡的边缘就会产生波浪状、圆形、锯齿和闪烁等有损现象,严重影响了画面的质量。全屏反锯齿全屏反锯齿(fullsceneAnti-aliasing,简称FSAA),也称全屏抗锯齿,它指的是利用反锯齿技术对输出到...
· 波拉波拉岛
影视作品电影限制级战警(xXx)里最后一幕,范·迪塞尔在水上屋里度假之场景。电影伴侣度假村(CouplesRetreat)里的“伊甸岛渡假村”(或称伊甸园渡假村)取景地。参考文献
· 波波尔·乌

简介此书一开始为马雅文明的创世神话,紧接着是马雅双胞胎英雄乌纳普及斯巴兰克这两位在马雅神话中极重要角色的故事。《波波尔·乌》之后又围绕在王族以及欲以神力维持统治的众神身上,详细描述了基切人的历史与建国基础。以下为此创世神话初章的第一句,以现代的拼字系统与标点符号书写:历史席梅内兹神父的手稿包含了《波波尔·乌》最早的文献。内容由基切语及西班牙文写成。《波波尔·乌》最著名且最完整的手稿是以基切语书写成的。西班牙人在征服危地马拉之后,禁止了马雅文字的使用,并开始拉丁文字的教授;但一些马雅的祭司和书记仍偷偷地以马雅文字抄写一些古老典籍,其中一份《波波尔·乌》的手抄本于1702年为一位神父法兰西斯可‧席梅内兹(FranciscoXiménez)在危地马拉一个小镇奇奇卡斯德南哥发现。席梅内兹并没有将之烧毁,反而将它抄写下来,又将之翻译成西班牙文。席梅内兹神父的手抄本与翻译本一直被世人遗忘在危地马拉市圣...
· 林波波省
历史地理人口经济国家公园北部的克鲁格国家公园是林波波省最大的吸引力之一。这个2万公顷的保护区横跨全省东部地区,是南非、莫桑比克和津巴布韦之间大林波波跨界公园的一部分。这里拥有成百上千种树木、鱼类、两栖动物、爬行动物、鸟类和哺乳动物,其中包括非洲五大动物。步行或驱车观看猎物、远足、生态旅行和山地自行车等旅游路线为游客探索这个野性荒原提供了奇妙的方法。在全省其他50多个公园和自然保护区内也可以享受到类似的活动。重要市镇波罗克瓦尼(Polokwane)Thohoyandou行政区划CapricornDistrictMopaniDistrictSekhukhuneDistrictVhembeDistrictWaterbergDistrict教育交通重要机场重要高速公路体育
· 波
数学描述在数学上,任何一个沿某一方向运动的函数形状都可以认为是一个波。考虑一种最简单的情况:二维平面波,波的形状可以用xy{\displaystylexy}平面上的曲线y=f(x){\displaystyley=f(x)}描述。如果这个曲线沿着x{\displaystylex}轴以ωω-->{\displaystyle\omega}的速度向右运动,不难看出,这样的函数应该满足如下方程:y=f(x−−-->ωω-->t){\displaystyley=f(x-\omegat)}如果沿x轴以ω的速度向左运动,则为:y=f(x+ωω-->t){\displaystyley=f(x+\omegat)}以上两个方程都满足如下形式的微分方程:这里c通常是一个固定常数,代表波的传播速率。这个方程称为一维波动方程。它的通解可以表示为:它表示一个向左传播的波和一个向右传播的波的叠加。...
关于我们

关注族谱网 微信公众号,每日及时查看相关推荐,订阅互动等。
APP下载

下载族谱APP 微信公众号,每日及时查看

扫一扫添加客服微信















