涡旋-族谱新闻-族谱网

涡旋

2020-10-16

出处：族谱网

作者：阿族小谱

浏览:752次

转发:0次

评论:0

性质飞机云中的克劳不稳定性（英语：CrowInstability）产生了涡旋。涡量涡旋的动力学基本概念是涡量，这是描述流体中观测者所见特定一点上旋转运动的矢量。概念上涡量可以透过放置一个小粗糙球体放在要观测的点，并且让该球随流体运动以观察它如何环绕涡旋的轴心。涡量矢量的方向将是想像的球体旋转方向的轴方向（根据右手定则），而矢量长度将正比（2倍）于球体的角速度。数学上，涡量被定义为流体速度场的旋度，通常以ωω-->→→-->{\displaystyle{\vec{\omega}}}表示，并相等于矢量分析公式∇∇-->××-->u→→-->{\displaystyle\nabla\times{\vec{\mathit{u}}}}；∇∇-->{\displNabla算子\nabla}是Nabla算子，u→→-->{\displaystyle{\vec{\mathit{u}}}}则是区域流速。经由...

性质

飞机云中的克劳不稳定性（英语：Crow Instability）产生了涡旋。

涡量

涡旋的动力学基本概念是涡量，这是描述流体中观测者所见特定一点上旋转运动的矢量。概念上涡量可以透过放置一个小粗糙球体放在要观测的点，并且让该球随流体运动以观察它如何环绕涡旋的轴心。涡量矢量的方向将是想像的球体旋转方向的轴方向（根据右手定则），而矢量长度将正比（2倍）于球体的角速度。数学上，涡量被定义为流体速度场的旋度，通常以 ω ω --> → → --> {\displaystyle {\vec {\omega }}} 表示，并相等于矢量分析公式 ∇ ∇ --> × × --> u → → --> {\displaystyle \nabla \times {\vec {\mathit {u}}}} ； ∇ ∇ --> {\displNabla算子 \nabla } 是Nabla算子， u → → --> {\displaystyle {\vec {\mathit {u}}}} 则是区域流速。

经由涡量 ω ω --> → → --> {\displaystyle {\vec {\omega }}} 求得的区域性旋转量不可和相对外部环境或任何固定轴的区域性角速度矢量混淆。特别是在涡旋中涡量 ω ω --> → → --> {\displaystyle {\vec {\omega }}} 的方向可能和相对于涡旋线的流体平均角速度矢量相反。涡量的定义也不等于区域性流体的旋转速度，而是旋转速度的2倍。

涡量的数学意义

在涡旋中，涡量取决于随着和轴的距离r变化的流体速度u。有两个特殊的状况：

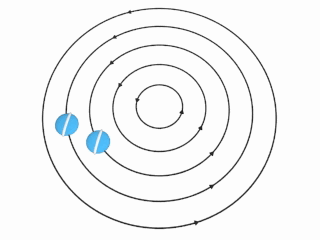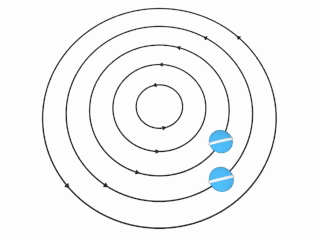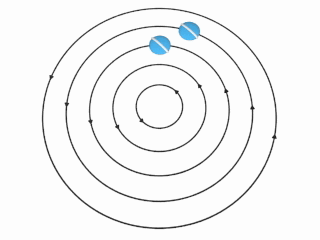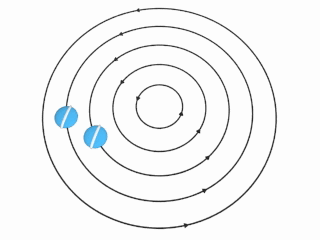
刚体（旋转）涡旋。

如果流体的转动类似刚体，即角速度Ω固定，则速度u将会随距离轴的距离r成正比。在这情况下的涡量在涡旋各处均相同：涡量方向平行于转轴，并且强度相等于相对转轴的固定角速度Ω的2倍。 Ω Ω --> → → --> = ( 0 , 0 , Ω Ω --> ) , r → → --> = ( x , y , 0 ) , {\displaystyle {\vec {\Omega }}=(0,0,\Omega ),\quad {\vec {r}}=(x,y,0),} u → → --> = Ω Ω --> → → --> × × --> r → → --> = ( − − --> Ω Ω --> y , Ω Ω --> x , 0 ) , {\displaystyle {\vec {u}}={\vec {\Omega }}\times {\vec {r}}=(-\Omega y,\Omega x,0),} ω ω --> → → --> = ∇ ∇ --> × × --> u → → --> = ( 0 , 0 , 2 Ω Ω --> ) = 2 Ω Ω --> → → --> {\displaystyle {\vec {\omega }}=\nabla \times {\vec {u}}=(0,0,2\Omega )=2{\vec {\Omega }}} 。

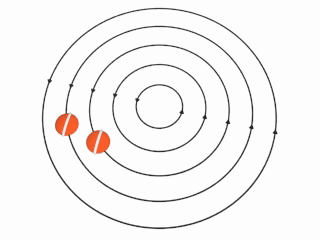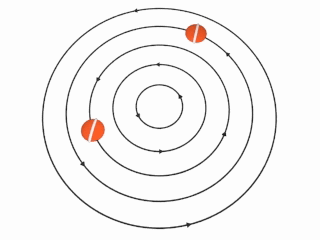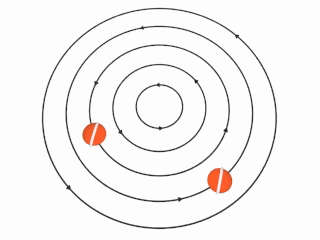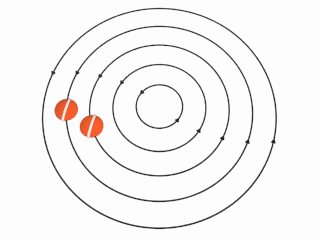
非旋涡旋。

如果转动速度u和距离轴距离r成反比，则右图中想像的球将不会自行转动：该球将会在环绕涡旋的轴进行原周运动时保持相同方向。这时涡量 ω ω --> → → --> {\displaystyle {\vec {\omega }}} 为在轴以外的任一处都为0，即为非旋流。 Ω Ω --> → → --> = ( 0 , 0 , α α --> r − − --> 2 ) , r → → --> = ( x , y , 0 ) , {\displaystyle {\vec {\Omega }}=(0,0,\alpha r^{-2}),\quad {\vec {r}}=(x,y,0),} u → → --> = Ω Ω --> → → --> × × --> r → → --> = ( − − --> α α --> y r − − --> 2 , α α --> x r − − --> 2 , 0 ) , {\displaystyle {\vec {u}}={\vec {\Omega }}\times {\vec {r}}=(-\alpha yr^{-2},\alpha xr^{-2},0),} ω ω --> → → --> = ∇ ∇ --> × × --> u → → --> = 0 {\displaystyle {\vec {\omega }}=\nabla \times {\vec {u}}=0} 。

非旋涡旋

在没有外力的情况下，涡旋通常会快速演变为非旋流，这时流速u与轴距离r成反比。因此非旋涡旋也称为“自由涡旋”。

在非旋涡旋中，沿着任何转轴不包含在内的封闭流线上的环量均为0；如包含转轴则有固定的值 Γ Γ --> {\displaystyle \Gamma } 。涡旋中特定一点的切向速度为 u θ θ --> = Γ Γ --> / ( 2 π π --> r ) {\displaystyle u_{\theta }=\Gamma /(2\pi r)} 。因此，相对转轴的单位质量角动量守恒，其值为 r u θ θ --> = Γ Γ --> / ( 2 π π --> ) {\displaystyle ru_{\theta }=\Gamma /(2\pi )} 。

然而，理想的非旋涡旋流实际上是不能实现的，因为它代表粒子的速度在接近涡旋线时会无边界限制地增加（并且需要有力量保持粒子在环状路径上）。实际上，真实的涡旋总是在接近轴的核心区域时粒子速度停止增加，并且在距离r为0时下降为0。这个区域就不再是非旋涡旋：涡量 ω ω --> → → --> {\displaystyle {\vec {\omega }}} 在该区内的值并非0，并且方向大致和兰金线平行。兰金涡旋（英语：Rankine vortex）是一个假设距离r的值低于固定距离r0时，内部区域为刚体旋转流，旋转核心外的区域为非旋流的模型。兰姆－奥辛涡旋（英语：Lamb-Oseen vortex）模型则是以纳维-斯托克斯方程描述的流体状态，并假设对称为圆柱型对称时的精确解。在此：

在非旋涡旋中，相邻流线中各流体的移动速度均不相同，因此会产生摩擦力造成能量损失，尤其是接近转轴的核心区域。

旋转涡旋

涡量远离中心轴即不为0的旋转涡旋可以只需要一些外力作用就能永久保持该状态，因此它不能由流体本身产生。

例如假设有一个水桶以固定角速度w环绕一个垂直轴，水最终会以刚体模式旋转。之后粒子会以圆形路径运动，速度u等于wr。在本例中，不受约束的水面将会呈现抛物面形状。

在这些状况下，刚体旋转的水桶外壳提供了一个额外的力，即方向向内的水的额外压力梯度，并且阻止了刚性涡旋流演变为无旋流。

涡旋几何

在一个固定的涡旋，典型的流线（流线任一处的切线都是速度矢量）是闭合的绕轴环线；并且每个涡旋线（涡旋线任一处的切线均为涡量矢量）大致和轴方向平行。在各处都是速度和涡量切平面的平面则被称为“涡旋管”（Vortex tube）。一般来说，涡旋管都围绕涡旋的转轴周围。轴本身也是其中一条涡旋线，并且涡旋管有直径为0的极限情况。

根据亥姆霍兹定理，涡旋线的起点或终点不可在流体内，除了旋涡正在形成或消失的短暂非定常流动时。一般情形下，涡旋线（尤其是轴线）不是封闭的环线就是在流体边界截止。涡流是涡旋线在流体边界截止的例子，即轴线在自由表面截止。涡旋管的涡旋线全都是封闭环线，因此外观上类似封闭的环面状表面。新形成的涡旋会快速伸展和弯曲以消除任何开放终端的涡旋线。例如当飞机引擎启动时，在螺旋桨或涡轮扇发动机前方经常会形成涡旋。这时涡旋线的其中一个端点在引擎上，另一个端点会随着涡旋伸展和弯曲直到接触地表为止。

当使用烟雾或墨水使涡旋肉眼可见时，似乎可看到螺旋形的迹线和流线存在。事实上这是一个错觉，并且流体粒子是在封闭路径中移动的。被当成流线的螺旋状条纹实际上是原本跨越了数条流线的被标记的团块，并且因为非均匀的速度分布而延伸为螺旋状。这样的例子有星系的螺旋臂和热带风暴。

涡旋中的压力

在涡旋中运动的流体会产生动态压力（非流体静压力），并且根据伯努利定律，动态压力在接近轴心处最低，并随着与轴心距离增加。因此可以说压力梯度迫使流体环绕轴心弯曲运动。

在刚体涡旋中，流动的流体有固定的密度，动态压力和距离轴的距离r的平方成正比。在固定引力场中，如果自由表面存在，表面将呈现中央凹陷的抛物面。

在流体密度固定，且形状为圆柱对称的非旋涡旋流中，动态压力变化关系式为：P∞ − K/r。P∞是距离轴无线远处的压力。该公式提供了另一种限制核心区域范围的规则，因为压力不为负值。自由表面（如果存在的话）在靠近轴心的区域深度会快速下降，并且与r成反比。

空气中涡旋的核心有时候是可见的，这是因为在核心的低压和低温下因为凝结而形成水蒸气羽流，漏斗状的龙卷风就是一个典型的例子。当一条涡旋线在边界表面终止，压力的下降可能使物质从表面被带入核心。例如沙尘暴是沙被接触到地面的空气涡旋核心吸入核心。同样的道理，水中的涡旋如果在表面终止（例如在浴缸中形成的漩涡），也可能将空气吸入涡旋核心。停在地面的飞机从发动机向前沿伸出的涡旋也可将水和小石块吸入核心，再进入发动机。

涡旋的演变

机翼通过时产生的涡旋，在此以有色烟雾显示其存在。

涡旋不是稳定的，它们可以位移和改变形状。

在运动中的涡旋，粒子的路径不再是封闭的，而是类似螺旋或摆线的曲线。

涡流也可以和径向或轴向流合并。这时流线和迹线就不再是封闭曲线，而分别是螺线或螺旋。这样的例子分别是龙卷风和排水漩涡的状况。带有螺旋流线的涡旋被称为螺线管。

只要黏性和扩散的影响可忽略不计，流体会随着移动的涡旋而运动。特别是在物质被限制在内部的核心区域在涡旋移动时相当容易留在内部，这是亥姆霍兹第二定理的结果。因此，和面波以及P波不同的是涡旋可以将质量、能量以及动量传递到相对于涡旋本身相当大的距离，并且扩散程度令人惊讶地少。这效应可在烟圈、涡环玩具（英语：Vortex ring toy）和涡环枪（英语：Vortex ring gun）看到。

2个以上涡旋如果大致平行，并且以相同方向旋转的话，将会互相吸引，最后合并为单一涡旋，并且合并后的环量将是合并前所有涡旋环量的总和。例如产生上升力机翼会在其后缘产生一系列的小涡旋。这些小型的涡旋会合并为一个大型的翼尖涡流，而翼尖涡流环量小于翼弦边缘的下降流。这个现象也会发生在其他运动中的翼型，例如螺旋桨叶片。另一方面，两个平行但旋转方向相反的涡流（例如飞机的2个翼尖涡流）则倾向分离。

涡旋包含了流体圆周运动的巨大能量。在理想流体中能量永远不会消散，并且涡旋将永远保持下去。然而，真正的流体有黏度，将使流体从核心区域开始缓慢消散能量。只有透过因为黏度让涡旋消散能量才能让涡旋线的终点在流体中，而非流体边界。

2维模型

当粒子的速度被限制为平行于一个固定平面的方向，就可忽略垂直于平面的空间矢量分量，并且将流体的速度场模型建立于该平面上。接着涡量矢量 ω ω --> → → --> {\displaystyle {\vec {\omega }}} 的方向永远垂直于平面，并且被认为是标量。这样的假设有时在气象学上研究类似热带风暴尺度大器现象时使用。

这样背景下的涡流行为在许多方面和真实状况适不同的。例如在3维的涡旋伸展是不被允许的。

更进一步的例子

土星六角形（英语：Saturn"s hexagon），位于土星北极的云涡旋。

C-17运输机在潮湿跑道上以低速启动高功率引擎时所见的涡旋。

电磁场的行为如以流体动力学解释，特定方向电流体的加速度运动会产生磁流体的正向涡旋。并且磁流体本身周围会产生负向电涡旋。经典非线性磁方程的精确解包含了朗道－利夫希茨模型（英语：Landau–Lifshitz model）、连续性的经典海森堡模型（英语：Classical Heisenberg model）、石森方程（英语：Ishimori equation），以及非线性薛定谔方程（英语：Nonlinear Schrödinger equation）。

泡沫环是水下的涡环，并且核心部分有泡沫环存在。泡沫环有时候由鲸豚产生。

飞机的机翼、螺旋桨叶片、帆和其他种翼的升力可解释为产生的涡旋叠加在通过翼的流体上。

气动阻力（英语：Aerodynamic drag）可以解释为移动物体周围产生大量涡旋，并且使物体的动能散失。

在特定海峡或海湾中可以因为海洋潮汐而形成巨大漩涡。例如神话中墨西拿海峡的卡律布狄斯、日本鸣门海峡的鸣门漩涡、挪威罗弗敦群岛的强涡流。

地球大气层中的涡旋是重要的气象现象。这些现象包含了包含小至数公里的龙卷风、海龙卷风，大至数百公里的热带气旋等中尺度气旋（英语：Mesocyclone）。这些涡旋的动能来自随高度而变化的高度和大气湿度差异。热带气旋的旋转方向受到地球自转影响。另一个例子就是中心在地球极地附近的极地涡旋，它是在中高层对流层和平流层内的持续性大规模天气现象。

其他行星的大气层中，涡旋也是相当明显的气候特征。例如木星大气层中持续存在的大红斑、海王星大气层中间歇存在的大黑斑、火星上的尘卷风，以及土星北极的土星六角形（英语：Saturn"s hexagon）。

太阳黑子是太阳光球的黑暗区域，其温度较周围低，并且有强烈磁场活动。

黑洞或其他巨大引力源天体周围的吸积盘。

参见