简介在日本（15年，历代2名）进入TOP10的单一连续的记录，从1990年直到2004年。表共21,000,000专辑，唱片销售总量超过40万份，包括单。专辑的总销量在过去的许多艺术家，在17日也。此外，因为这张专辑在ORICON每周图表达到3名“，在”太阳的季节“于1986年（27年，历代2名）记录在不断的连续进入TOP10的专辑至今（仍在更新）有。成员前田亘辉（英名:MaedaNobuteru）―1965年4月23日-生于日本神奈川县厚木市。血型A型春畑道哉（英名:HaruhataMichiya）―1966年11月5日-生于日本东京都町田市。血型A型角野秀行（英名:KakunoHideyuki）―1965年7月6日-生于日本神奈川县座间市。血型A型松本玲二（英名:MatsumotoRyoji）―1966年5月30日-生于日本神奈川县座间市。血型AB型音楽活动TUBE属于BMF公司198...

生平夏之蓉为雍正四年（1726年）丙午科举人，授盐城教谕。雍正十一年（1733年）中式癸丑科第二甲第三十五名进士。乾隆元年（1736年）召试博学宏词，列二等，授翰林院检讨。乾隆三年（1738年）任一统志馆纂修官。乾隆九年（1744年）任甲子科福建乡试正考官，次年授广东学政。乾隆十三年（1748年）改湖南学政。《清史稿》有传。著作《读史提要录》十二卷《半舫斋偶辑》四卷《半舫斋诗文集》《半舫斋古文》八卷《半舫斋诗诗钞》二十卷《駪征集》四卷《诸经考辨》二十卷《慎道篇》《汲古篇》《酌雅集》《正味集》《兴艺录》主修《高邮州志》主修《通州志》相关条目夏之芳：夏之蓉二哥，曾任巡台御史。夏廷芝：夏之蓉之弟，排行老四，亦是雍正癸丑科进士（第二甲第三十六名）注释及参考资料《清史列传》九册卷七十一,55《清国史馆传稿》4348号,4616号,4634号,6946号,7912号中央研究院历史语言研究所内阁大库档案...

用途吴大溦认为夏后氏之璜不是佩戴用的璜，而是一种大璜，为礼神之玉。《山海经·海外西经》记载，“大乐之野，夏后启于此儛九代，乘两龙，云盖三层。左手操翳，右手操环，佩玉璜。在大运山北。”陈剩勇认为夏后氏在扮演天地的巫觋时佩戴玉璜，那么这种璜就不是一般的佩饰，而是沟通生死世界的一种宗教法器。易仁认为红山文化出土的勾云形玉珮就是夏代的璜，早期寓意为生殖崇拜，晚期为王权和地位的象征。鲁国的夏后氏之璜周初大封建的时候，鲁公伯禽分到了大路、大旗、夏后氏之璜、封父之繁弱等宝物。这些宝物成为鲁国的国宝，世代由鲁国国君掌管。前502年冬季，阳虎作乱失败，他进入公宫，拿走了夏后氏之璜和封父之繁弱，逃亡到五父之衢。前501年夏季，阳虎将夏后氏之璜和封父之繁弱送回鲁国。宋国的夏后氏之璜前481年，宋国的桓魋在作乱失败后逃亡到卫国，卫国的公文氏攻打桓魋，向他索取夏后氏之璜。桓魋给了公文氏别的玉器后逃到齐国。其他《淮南

写作背景和年代穆尔和妻子哈莉特·泰勒早在1854年就把这本书的主题列入了他们未来的写作计划。1854-1855年冬天，当穆尔在欧洲旅行时，他开始专注于将这一主题独立成书的想法。基本上可以确定，这本书的初稿主干是在1856-1857年间完成的。穆勒在他的《自传》中提到，他和妻子在此之后多次反复修改润色。穆勒自己说：“我的作品中，没有哪本是像它一样谨慎地写作、细致地修改。”原定一八五八年穆勒从印度事务部退休后，这本书的终稿会确定下来，但那年晚些时候穆勒妻子的死亡让他决定不再继续修改。尽管穆勒通常会于再版中大规模的进行修改，但他认为《论自由》是追忆妻子的“献祭”：“我没有做任何的补充或者修改，我永远也不会。”内容目录严复翻译，上海三联书店出版首篇引论篇二释思想言论自繇篇三释行己自繇明特操为民德之本篇四论国群小己权限之分界篇五论自繇大义之施行康慨翻译，湖南文艺出版社出版第一章引论第二章论思想自由和...

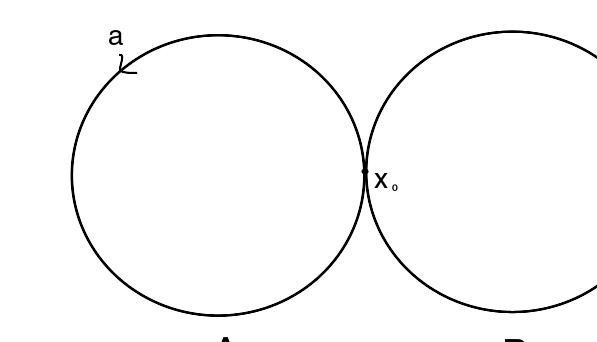
历史在1882年，WaltherDyck在发表于MathematischeAnnalen的论文GruppentheoretischeStudien中研究了自由群的概念，但未加以命名。“自由群”一词由JakobNielsen于1924年引入。例子2个圆环的集丛整数的加法群(Z,+){\displaystyle(\mathbb{Z},+)}是自由群；事实上我们可取S:={1}{\displaystyleS:=\{1\}}。在巴拿赫-塔斯基悖论的论证中用到两个生成元的自由群，以下将予说明。在代数拓扑学中，k{\displaystylek}个圆环的集丛（即：k{\displaystylek}个只交于一点的圆环，见右图）的基本群是k{\displaystylek}个生成元的自由群。建构方式今将构造集合S{\displaystyleS}上之自由群F(S){\displaystyleF(S)}，分解动作...