群的子集的乘积

在随后的讨论中，我们将使用在 G 的子集上的二元运算：如果给出 G 的两个子集 S 和 T ，我们定义它们的乘积为 ST = { st : s ∈ S 并且 t ∈ T }。这个运算是符合结合律的并有单位元为单元素集合{ e }，这里的 e 是 G 的单位元。因此， G 的所有子集的集合形成了在这个运算下的幺半群。

凭借这个运算我们可以首先解释商群是什么，并接着解释正规子群是什么：

它完全由包含 e 的子集所确定。 G 的正规子群是在任何这种划分中包含 e 的集合。在划分中的子集是这个正规子群的陪集。

群 G 的子群 N 是正规子群，当且仅当陪集等式 aN = Na 对于所有 G 中的 a 都成立。依据上述定义的在子集上的二元运算， G 的正规子群是交换于 G 的所有子集的子群，并指示为 N ⊲ G 。置换于 G 的所有子群的子群叫做可置换子群。

定义

设 N 是群 G 的正规子群。我们定义集合 G / N 是 N 在 G 中的所有左陪集的集合，就是说 G / N = { aN : a ∈ G }。在 G / N 上的群运算定义如上。换句话说，对于每个 G / N 中 aN 和 bN ， aN 和 bN 的乘积是 ( aN )（ bN ）。这个运算是闭合的，因为 ( aN )( bN )实际上是左陪集：

N 的正规性被用在了这个等式中。因为 N 的正规性， N 在 G 中的左陪集和右陪集是相等的，所以 G / N 也可以定义为 N 在 G 中所有的右陪集的集合。因为运算是从 G 的子集的乘积得出的，这个运算是良好定义的（不依赖于表示的特定选择），符合结合律的，并有单位元 N 。 G / N 的元素 aN 的逆元是 a N 。

定义的动机

G / N 叫做商群的理由来自整数的除法。在12除以3的时候得到答案4是因为我们可以把12个对象重新分组为3个对象的4个子搜集。商群出于同样想法，但用一个群作为最终答案而非一个数，因为群要比对象的随机搜集要更有结构。

更细致的说，在查看 G / N 而 N 是 G 的正规子群的时候，这个群结构形成一种自然“重新分组”。它们是 N 在 G 中陪集。因为我们从一个群和正规子群得到的最终的商包含比只是陪集的（正常除法所产生的）数目要更多的信息，这里得到了一个群结构自身。

例子

考虑整数集 Z （在加法下）的群和所有偶数构成的子群2 Z 。这是个正规子群，因为 Z 是阿贝尔群。只有两个陪集：偶数的集合和奇数的集合；因此商群 Z /2 Z 是两个元素的循环群。这个商群同构于集合{ 0, 1 }带有模2加法运算的群；非正式的说，有时称 Z /2 Z 等于集合{ 0, 1 }带有模2加法。

上个例子的稍微一般化。再次考虑整数集 Z 在加法下的群。设 n 是任何正整数。我们考虑由 n 的所有倍数构成的 Z 的子群 n Z 。 n Z 在 Z 中还是正规子群因为 Z 是阿贝尔群。陪集们是搜集{ n Z ,1+ n Z ,...,( n −2)+ n Z ,( n −1)+ n Z }。整数 k 属于陪集 r + n Z ，这里的 r 是 k 除以 n 的馀数。商 Z / n Z 可以被认为模以 n 的“馀数”的群。这是个 n 阶循环群。

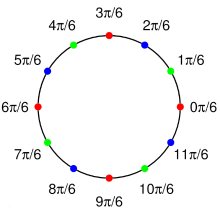
N 在 G 中的陪集

考虑复数十二次单位一的根的乘法阿贝尔群 G ，它们是在单位圆上的点，它们在右图中展示为着色的球并在每点上用数标记出它们的辐角。考虑它由单位一的四次根构成的子群 N ，在图中表示为红色球。这个正规子群把群分解为三个陪集，分别表示为红色、绿色和蓝色。你可以验证这些陪集形成了三个元素的群（红色元素和蓝色元素的乘积是蓝色元素，蓝色元素的逆元是绿色元素等等）。因此商群 G / N 是三种颜色元素的群，它又是三个元素的循环群。

考虑实数集 R 在加法下的群，和整数集子群 Z 。 Z 在 R 中的陪集们是形如 a + Z 的所有集合，这里0 ≤ a < 1是实数。这种陪集的加法是通过做相应的实数的加法，并在结果大于或等于1的时候减去1完成的。商群 R / Z 同构于圆群S 绝对值绝对值为1的复数在乘法下的群，或者说关于原点旋转维旋转的群，也就正交群正交群SO(2)。有一个同构给出为 f ( a + Z ) = exp（2 πia 欧拉恒等式恒等式）。

如果 G 是可逆的3 × 3实数矩阵的群，而 N 是带有行列式为1的3 × 3实数矩阵的子群，那么 N 在 G 中是正规子群（因为它是行列式同态的核）。 N 的陪集们是带有给定行列式的矩阵的集合们，因此 G / N 同构于非零实数的乘法群。

考虑阿贝尔群 Z 4 = Z /4 Z （也就是集合{ 0, 1, 2, 3 }带有加法模4），和它的子群{ 0, 2 }。商群 Z 4 / { 0, 2 }是{ { 0, 2 }, { 1, 3 } }。这是带有单位元{ 0, 2 }的群，群运算如{ 0, 2 } + { 1, 3 } = { 1, 3 }。子群{ 0, 2 }和商群{ { 0, 2 }, { 1, 3 } }同构于 Z 2 。

考虑乘法群 G = Z n 2 ∗ ∗ --> {\displaystyle G=\mathbf {Z} _{n^{2}}^{*}} 。第 n 个馀数的集合 N 是 Z n ∗ ∗ --> {\displaystyle \mathbf {Z} _{n}^{*}} 的ϕ ( n )阶乘法子群。则 N 在 G 中是正规子群并且因子群 G / N 有陪集 N ,（1+ n ） N , (1+ n ) N,…,(1+ n ) N。Pallier加密系统基于了在不知道 n 的因子分解的时候难于确定 G 的随机猜想的陪集的猜想。

性质

商群 G / G 同构于平凡群（只有一个元素的群），而 G / { e }同构于 G 。

G / N 的阶定义为等于[ G : N ]，它是 N 在 G 中的子群的指标（index）。如果 G 是有限的，这个指标还等于 G 的阶除以 N 的阶。注意 G / N 可以在 G 和 N 二者是无限的时候是有限的（比如 Z / 2 Z ）。

有一个“自然”满射群同态 π : G → G / N ，把每个 G 的元素 g 映射到 g 所属于的 N 的陪集上，也就是： π ( g ) = gN 。映射 π 有时叫做“G到G / N上的规范投影”。它的核是 N 。

在包含 N 的 G 的子群和 G / N 的子群之间有一个双射映射；如果 H 是包含 N 的 G 的子群，则对应的 G / N 的子群是 π ( H )。这个映射对于 G 的正规子群和 G / N 也成立，并在格定理中形式化。

商群的一些重要性质记录在同态基本定理和同构基本定理中。

如果 G 是阿贝尔群、幂零群或可解群，则 G / N 也是。

如果 G 是循环群或有限生成群，则 G / N 也是。

如果 N 被包含在 G 的中心内，则 G 也叫做这个商群的中心扩张。

如果 H 是在有限群 G 中的子群，并且 H 的阶是 G 的阶的一半，则 H 保证是正规子群，因此 G / H 存在并同构于 C 2 。这个结果还可以陈述为“任何指标为2的子群都是正规子群”，并且它的这种形式还适用于无限群。

所有群都同构于一个自由群的商。

有时但非必然的，群 G 可以从 G / N 和 N 重构为一个直积或半直积。判定何时成立的问题叫做扩张问题。不成立的一个例子如下。 Z 4 / { 0, 2 }同构于 Z 2 ，并且还同构于{ 0, 2 }，但是唯一的半直积是直积，因为 Z 2 只有一个平凡的自同构。所以 Z 4 不同于 Z 2 × Z 2 ，它不能被重构。

参见

商环，也叫做因子环

群扩张

格定理

商范畴

短正合序列

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。