



有限状态机
概念和术语
状态存储关于过去的信息,就是说:它反映从系统开始到现在时刻的输入变化。转移指示状态变更,并且用必须满足确使转移发生的条件来描述它。动作是在给定时刻要进行的活动的描述。有多种类型的动作:
FSM(有限状态机)可以使用上面图1那样的状态图(或状态转移图)来表示。此外可以使用多种类型的状态转移表。下面展示最常见的表示:当前状态(B)和条件(Y)的组合指示出下一个状态(C)。完整的动作信息可以只使用脚注来增加。包括完整动作信息的FSM定义可以使用状态表。
除了建模这里介绍的反应系统之外,有限状态自动机在很多不同领域中是重要的,包括电子工程、语言学、计算机科学、哲学、生物学、数学和逻辑学。有限状态机是在自动机理论和计算理论中研究的一类自动机。在计算机科学中,有限状态机被广泛用于建模应用行为、硬件电路系统设计、软件工程,编译器、网络协议、和计算与语言的研究。
分类
有两个不同的群组:接受器/识别器和变换器。
接受器和识别器
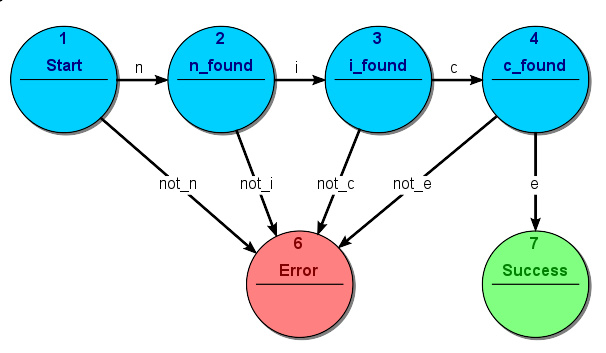
图2接受器FSM:解析单词"nice"
接受器 和 识别器 (也叫做 序列检测器 )产生一个二元输出,说要么“是”要么“否”来回答输入是否被机器接受。所有FSM的状态被称为要么接受要么不接受。在所有输入都被处理了的时候,如果当前状态是接受状态,输入被接受,否则被拒绝。作为规则,输入是符号(字符);动作不使用。图2中的例子展示了接受单词"nice"的有限状态自动机,在这个FSM中唯一的接受状态是状态7。
机器还可以被描述为定义了一个语言,它包含了这个机器所接受而非拒绝的所有字词;我们称这个语言被这个机器接受。通过定义,FSM接受的语言是正则语言- 就是说,如果一个语言被某个FSM接受,那么它是正则的(cf. Kleene的定理)。
开始状态
开始状态通常用“没有起点的箭头”指向它来表示(Sipser (2006)p.34)
接受(最终)状态
接受状态 (或称 最终状态 )是一个机器回报到目前为止,输入字符串属于它所接受的内容之状态。状态图中通常将其标示为双圆圈。 开始状态也可以是接受状态,此情况下自动机会接受空字符串。如果开始状态不是接受状态,且没有可以连到任何接受状态的箭头,那么此自动机就不会“接受”任何输入。 一个接受状态的例子如图3:一台判断输入二进位字符串是否含有偶数个0的确定有限自动机(DFA)。S 1 代表着已经输入了偶数个0,因此 S 1 即为接受状态(同时亦为开始状态)。若输入含有偶数个0(包含没有0的字符串),则此机器会以接受状态来结束。 被这台DFA接受的字符串,举例来说是ε(空字符串), 1, 11, 11…, 00, 010, 1010, 10110…等等。
变换器
变换器使用动作基于给定输入和/或状态生成输出。它们用于控制应用。常分为两种类型:
Moore机
只使用进入动作的FSM,就是说输出只依赖于状态。Moore模型的好处是行为的简单性。图1的例子展示了一个电梯门的Moore FSM。这个状态机识别两个命令:“command_open”和“command_close”触发状态变更。在状态“Opening”中的进入动作 (E:)开启电机开门,在状态“Closing”中的进入动作以反方向开启电机关门。状态“Opened”和“Closed”不进行任何动作。它们信号通知外部世界(比如其他状态机)情况:“门开着”或“门关着”。
Mealy机
图4变换器FSM: Mealy模型例子
只使用输入动作的FSM,就是说输出依赖于输入和状态。Mealy FSM的使用经常导致状态数目的简约。在图4中的例子展示了实现同上面Moore机同样行为的Mealy FSM(行为依赖于实现的FSM执行模型,比如对虚拟FSM可工作但对事件驱动FSM不行)。有两个输入动作(I:):“开启电机关门如果command_close下达”和“反向开启电机开门如果command_open下达”。
在实践中经常使用混合模型。
进一步可区分为 确定型 (DFA)和 非确定型 (NDFA、GNFA)自动机。在确定型自动机中,每个状态对每个可能输入只有精确的一个转移。在非确定型自动机中,给定状态对给定可能输入可以没有或有多于一个转移。这个区分在实践而非理论中更有用,因为存在算法把任何NDFA转换成等价的DFA,尽管这种转换一般会增加自动机的复杂性。
只有一个状态的FSM叫做组合FSM并只使用输入动作。这个概念在多个FSM要一起工作的情况下是有用的,这时把纯组合部分看作一种形式的FSM来适合设计工具可能是方便的。
FSM逻辑
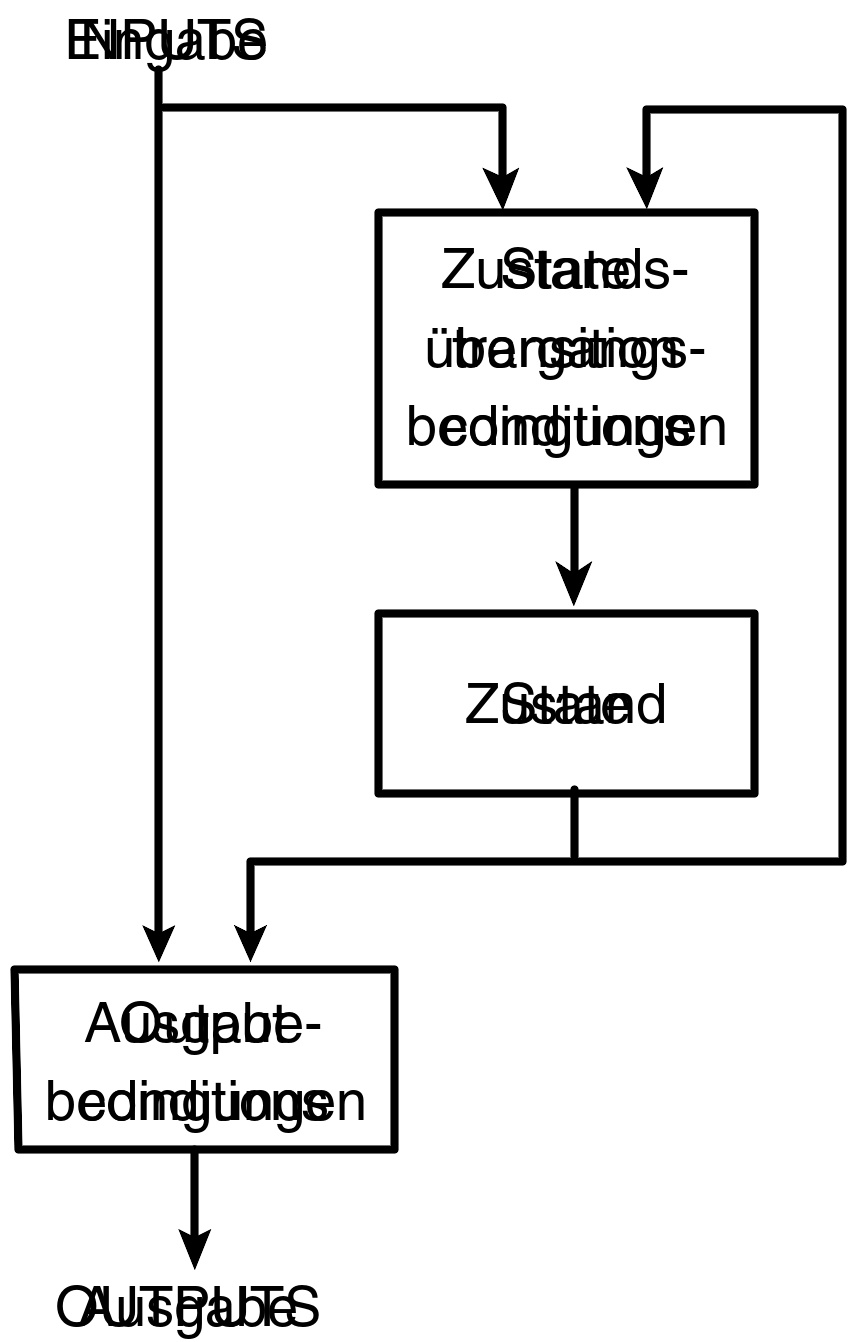
图5 FSM逻辑
FSM的下一个状态和输出是由输入和当前状态决定的。FSM逻辑在图5中展示。
数学模型
依据类型不同有多种定义。 接受器 有限状态机是五元组 ( Σ Σ --> , S , s 0 , δ δ --> , F ) {\displaystyle (\Sigma ,S,s_{0},\delta ,F)} ,这里的:
Σ Σ --> {\displaystyle \Sigma } 是输入字母表(符号的非空有限集合)。
S {\displaystyle S} 是状态的非空有限集合。
s 0 {\displaystyle s_{0}} 是初始状态,它是 S {\displaystyle S} 的元素。在非确定有限状态自动机中, s 0 {\displaystyle s_{0}} 是初始状态的集合。
δ δ --> {\displaystyle \delta } 是状态转移函数: δ δ --> : S × × --> Σ Σ --> → → --> S {\displaystyle \delta :S\times \Sigma \rightarrow S} 。
F {\displaystyle F} 是最终状态的集合, S {\displaystyle S} 的(可能为空)子集。
变换器 有限状态自动机是六元组 ( Σ Σ --> , Γ Γ --> , S , s 0 , δ δ --> , ω ω --> ) {\displaystyle (\Sigma ,\Gamma ,S,s_{0},\delta ,\omega )} ,这里的:
Σ Σ --> {\displaystyle \Sigma } 是输入字母表(符号的非空有限集合)。
Γ Γ --> {\displaystyle \Gamma } 是输出字母表(符号的非空有限集合)。
S {\displaystyle S} 是状态的非空有限集合。
s 0 {\displaystyle s_{0}} 是初始状态,它是 S {\displaystyle S} 的元素。在非确定有限状态自动机中, s 0 {\displaystyle s_{0}} 是初始状态的集合。
δ δ --> {\displaystyle \delta } 是状态转移函数: δ δ --> : S × × --> Σ Σ --> → → --> S {\displaystyle \delta :S\times \Sigma \rightarrow S} 。
ω ω --> {\displaystyle \omega } 是输出函数。
如果输出函数是状态和输入字母表的函数( ω ω --> : S × × --> Σ Σ --> → → --> Γ Γ --> {\displaystyle \omega :S\times \Sigma \rightarrow \Gamma } ),则定义对应于 Mealy模型 ,它可以建模为Mealy机。如果输出函数只依赖于状态 ( ω ω --> : S → → --> Γ Γ --> {\displaystyle \omega :S\rightarrow \Gamma } ),则定义对应于 Moore模型 ,它可建模为Moore机。根本没有输出函数的有限状态机叫做半自动机或转移系统。
优化
优化一个FSM意味着找到带有极小数目个状态的进行同样功能的机器。一种可能是使用蕴涵表或Moore简约过程。另一种可能是无环FSA的自底向上算法。
实现
硬件应用
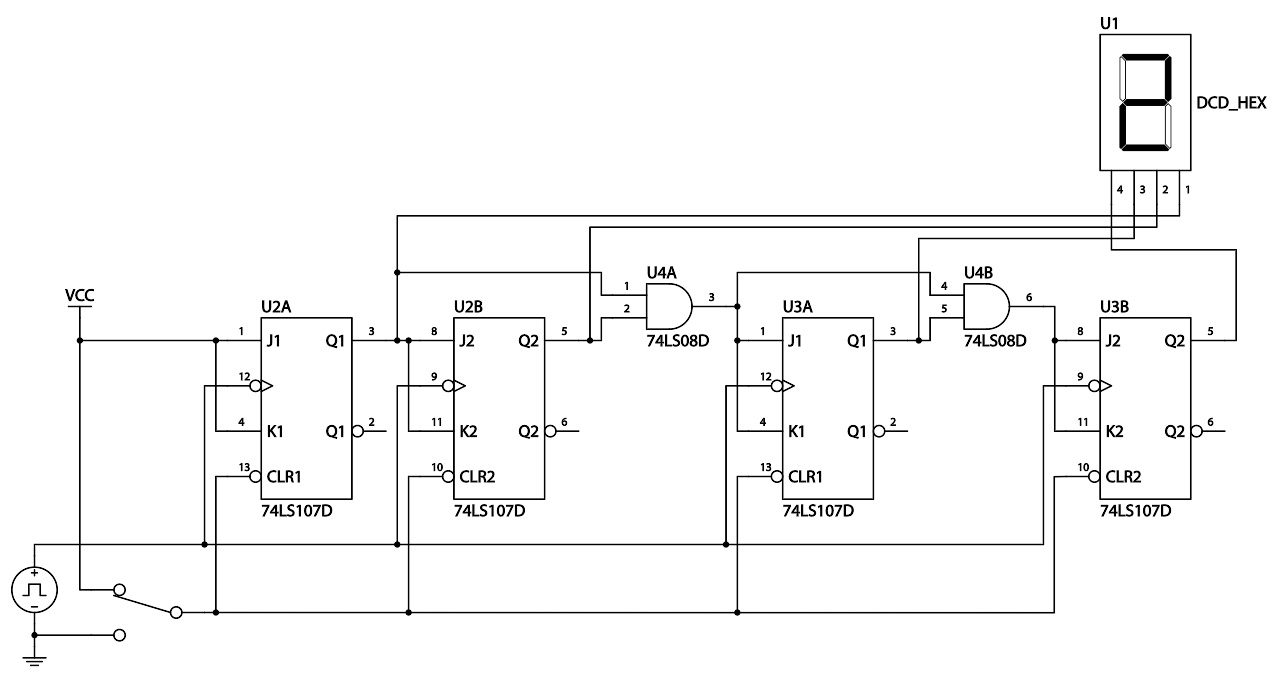
图6 4位TTL计数器的电路图
在数字电路中,FSM可以用可编程逻辑设备、可编程逻辑控制器、逻辑门和触发器或继电器来建造。更明确的说,硬件实现要求寄存器来存储状态变量,确定状态转移的一块组合逻辑,和确定FSM输出的另一块组合逻辑。一类经典硬件实现是Richard控制器。
软件应用
下列概念经常用来建造有有限状态机的软件应用:
事件驱动FSM
虚拟FSM (VFSM)
基于自动机编程
参考书目
Wagner, F., "Modeling Software with Finite State Machines: A Practical Approach", Auerbach Publications, 2006, ISBN 0-8493-8086-3.
Samek, M.,Practical Statecharts in C/C++, CMP Books, 2002, ISBN 1-57820-110-1.
Samek, M.,Practical UML Statecharts in C/C++, 2nd Edition, Newnes, 2008, ISBN 0-7506-8706-1.
Cassandras, C., Lafortune, S., "Introduction to Discrete Event Systems". Kluwer, 1999, ISBN 0-7923-8609-4.
Timothy Kam, Synthesis of Finite State Machines: Functional Optimization . Kluwer Academic Publishers, Boston 1997, ISBN 0-7923-9842-4
Tiziano Villa, Synthesis of Finite State Machines: Logic Optimization . Kluwer Academic Publishers, Boston 1997, ISBN 0-7923-9892-0
Carroll, J., Long, D. , Theory of Finite Automata with an Introduction to Formal Languages . Prentice Hall, Englewood Cliffs, 1989.
Kohavi, Z., Switching and Finite Automata Theory . McGraw-Hill, 1978.
Gill, A., Introduction to the Theory of Finite-state Machines . McGraw-Hill, 1962.
Ginsburg, S., An Introduction to Mathematical Machine Theory . Addison-Wesley, 1962.
参见
自动机
确定有限状态自动机
非确定有限状态自动机
Mealy机
Moore机
算法状态机
免责声明:以上内容版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。感谢每一位辛勤著写的作者,感谢每一位的分享。

- 有价值
- 一般般
- 没价值








推荐阅读
关于我们

APP下载


















