半加器

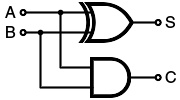
一位半加器的符号

半加器的功能是将两个一位二进制数相加。它具有两个输入和两个输出（分别是和、进位）。输出的进位信号代表了输入两个数相加溢出的高一位数值。因此，这两2个一位二级制数的和等于 2 C + S 。根据两个一位二进制数相加的结果，可以通过真值表、卡诺图得到右图所描绘的简易半加器设计。它使用了一个异或门来产生和 S ，并使用了一个与门来产生进位信号 C 。如果再添加一个或门来接收低位的进位输出信号，则两个半加器就构成了一个全加器。

半加器将两个输入位加和，产生进位与和，是半加器的两个输出。半加器的输入变量叫做被加数或被加位。输出变量为和与进位。半加器的真值表如下：

全加器

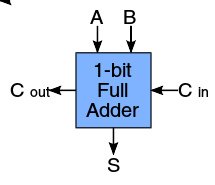
一位全加器的符号，它与半加器不同之处在于它还能接收一个低位进位输入信号 C in 。图中的蓝框是为了表明它作为一个整体可以级联构成多位二进制数的加法器。

全加器将两个一位二进制数相加，并根据接收到的低位进位信号，输出和、进位输出。全加器的三个输入信号为两个加数 A 、 B 和低位进位 C in 。 全加器通常可以通过级联（cascade）的方式，构成多位（如8位、16位、32位）二进制数加法器的基本部分。全加器的输出和半加器类似，包括向高位的进位信号 C out 和本位的和信号 S ，相加结果的总和表达为 s u m = 2 × × --> C o u t + S {\displaystyle \mathrm {sum} =2\times C_{out}+S} 。一位全加器的真值表为：

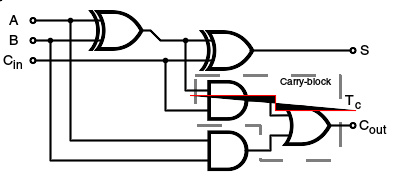
全加器的符号

在实际的应用中，全加器可以通过不同的方式制造，例如直接利用晶体管级的电路，或者由其他现成的逻辑门来构成。和、进位信号对应的逻辑函数表达式分别为 S = A ⊕ ⊕ --> B ⊕ ⊕ --> C i n {\displaystyle S=A\oplus B\oplus C_{in}} 以及 C o u t = ( A ⋅ ⋅ --> B ) + ( B ⋅ ⋅ --> C ) + ( A ⋅ ⋅ --> C ) {\displaystyle C_{out}=(A\cdot B)+(B\cdot C)+(A\cdot C)} 。另一种全加器电路与之前的方式略有不同，它用一个异或门来代替或门对其中两个输入信号进行求和，其进位信号对应的逻辑函数表达式分别为 C o u t = ( A ⋅ ⋅ --> B ) + ( C i n ⋅ ⋅ --> ( A ⊕ ⊕ --> B ) ) {\displaystyle C_{out}=(A\cdot B)+(C_{in}\cdot (A\oplus B))} 。通过适当的逻辑函数变化，可以证明它与前面的计算方法结果一致。

在这个实现中，将最后的或门换成异或门不会影响逻辑。如果电路使用的是每个芯片上只有一种闸的简单集成电路芯片，仅使用两种闸会比较方便。

全加器可以用两个半加器来构造，将输入端 A 和 B 连接到一个半加器上，然后将其和输出信号、进位输出信号分别作为第二个半加器的两个输入，并将两个进位输出信号进行逻辑或运算。全加器的关键路径（critical path，即经历最多逻辑门的路径）经过两个异或门，终止于和位 s {\displaystyle s} 。假定异或门耗费3个延迟来完成，一个全加器的关键路径上施加的延迟等于

进位模块(carry-block)包括2个闸，因此延迟为

全加器还可以使用一个三输入的异或门来求和，再使用一个两级与或结构来实现进位信号对应的积之和（sum of products）式。

更复杂的加法器

纹波进位加法器

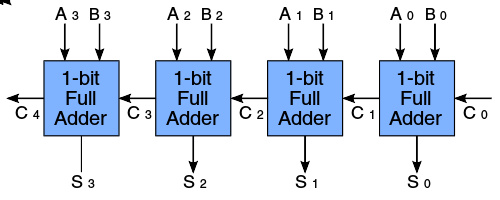
用四个一位全加器构成的四位纹波进位加法器

可以使用多个一位全加器来构成 N 位加法器，其中对应低位的全加器将其进位输出信号 C out 连接到高一位的全加器的进入输入端 C in 。这种构成多位加法器的形式被称为“纹波进位加法器（ripple-carry adder）”，“纹波”形象地描述了进位信号依次向前传递的情形。如果不需要连接其他进位信号，则最低位的全加器可以用半加器替换。

脉动进位加法器（纹波进位加法器）的电路布局形式较为简单，设计这种电路花费时间较短。然而，纹波进位加法器的进位输出、输入所经过的路径上比其他布局方式具有较多的逻辑门，高位的计算必须等待低位的进位输出信号被计算出来才能开始，因此造成了更大的延迟时间。

下面简单计算信号在加法器中的延迟。每一个全加器具有三级逻辑函数。在一个32位的纹波进位加法器中，有32个全加器，随之产生的逻辑门延迟则可以根据关键路径的延迟时间来决定，即2倍的最高位全加器输入信号、进位输出延迟，加上31乘以3倍的其他全加器上的延迟，总共等于95倍的逻辑门延迟。一个 n 位纹波进位加法器的最坏情形延迟方程为

从位位置0到进位输出的进位有一点不同：

输入进位必须经过 n 个进位生成器模块来得到进位输出的效果

交替进位极性和优化的 与或非门 （ 英语 ： AND-OR-Invert ） 的设计可以减少一半的延迟时间。

超前进位加法器

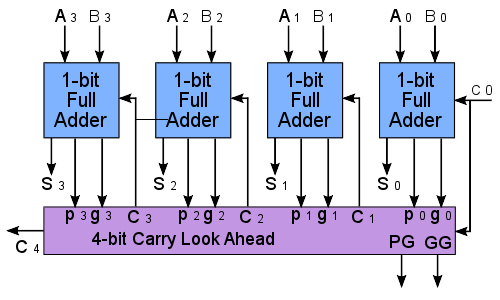
四位超前进位加法器

为了减少多位二进制数加减计算所需的时间，工程师设计了一种比脉动进位加法器速度更快的加法器电路，这种加法器被称为“超前进位加法器（carry-lookahead adder）”。

下面简述超前进位加法器的主要原理。 我们先来考虑构成多位加法器的单个全加器从其低一位获得的进位信号 c i + 1 = ( x i ⋅ ⋅ --> y i ) + ( x i ⋅ ⋅ --> c i ) + ( y i ⋅ ⋅ --> c i ) {\displaystyle c_{i+1}=(x_{i}\cdot y_{i})+(x_{i}\cdot c_{i})+(y_{i}\cdot c_{i})} ，我们可以将它变换为 c i + 1 = ( x i ⋅ ⋅ --> y i ) + ( x i ⊕ ⊕ --> y i ) ⋅ ⋅ --> c i {\displaystyle c_{i+1}=(x_{i}\cdot y_{i})+(x_{i}\oplus y_{i})\cdot c_{i}} 。现在为二级制数的每一位构建两个新信号：

生成（Generate）信号： G i = x i ⋅ ⋅ --> y i {\displaystyle G_{i}=x_{i}\cdot y_{i}}

传输（Propagate）信号： P i = x i ⊕ ⊕ --> y i {\displaystyle P_{i}=x_{i}\oplus y_{i}}

于是，某位全加器从低一位获得的进位可以表示为 c i + 1 = G i + P i ⋅ ⋅ --> c i {\displaystyle c_{i+1}=G_{i}+P_{i}\cdot c_{i}} ，例如次低位全加器从最低位获得的进位为 c 1 = G 0 + P 0 ⋅ ⋅ --> c 0 {\displaystyle c_{1}=G_{0}+P_{0}\cdot c_{0}} ，而从最低位开始第三位的那个全加器获得的进位信号则为 c 2 = G 1 + P 1 ⋅ ⋅ --> c 1 {\displaystyle c_{2}=G_{1}+P_{1}\cdot c_{1}} 。在多位脉动进位加法器中， c 2 {\displaystyle c_{2}} 必须连接到低一位的进位输出信号，如果使用这种方式构成多位全加器，则逻辑门的延迟会发生累加，导致降低电路的计算效率下降。超前进位加法器采取的方式是，将 c 1 {\displaystyle c_{1}} 的逻辑函数代入到 c 2 {\displaystyle c_{2}} ，即 c 2 = G 1 + P 1 ⋅ ⋅ --> ( G 0 + P 0 ⋅ ⋅ --> c 0 ) {\displaystyle c_{2}=G_{1}+P_{1}\cdot (G_{0}+P_{0}\cdot c_{0})} ，于是，这一位的进位输出就只取决于 x 1 {\displaystyle x_{1}} 、 y 1 {\displaystyle y_{1}} 、 x 0 {\displaystyle x_{0}} 、 y 0 {\displaystyle y_{0}} 、 c 0 {\displaystyle c_{0}} 几个信号，而这几个信号都是计算电路外部的已知信号，而非低一位的计算结果。上面考虑的是从最低位开始第三位的情况。采用类似的代入方法，可以用各位的生成信号 G i {\displaystyle G_{i}} 、传输信号 P i {\displaystyle P_{i}} ，以及最低位从外部获取的进位信号 c 0 {\displaystyle c_{0}} 来表示多位全加器的所有进位信号。

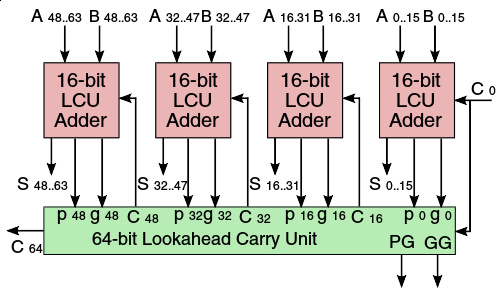
六十四位全加器可以逻辑划分为四个十六位超前进位加法器

通过列出多位加法器各位的进位输出，可以发现高位的进位输出表达式（积之和式）涉及的变量更多，对应的逻辑电路连线会变得更复杂，而且在实际应用中会遭遇逻辑门的扇入问题。因此有必要对位数过高的全加器进行逻辑划分，如将六十四位全加器分为四个十六位超前进位加法器来实现（如右图）。多位二进制数加法器的标准芯片通常具有超前进位的组成形式，例如7400系列的7483、74283芯片。

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。