例子和反例

函数g:R→ → -->R{\displaystyle g:\mathbb {R} \rightarrow \mathbb {R} }，定义为g(x)=x2{\displaystyle g(x)=x^{2}}，不是一个满射，因为，（举例）不存实数个实数满足x2=− − -->1{\displaystyle x^{2}=-1}。

但是，如果把g{\displaystyle g}的陪域限制到只有非负实数，则函数g{\displaystyle g}为满射。这是因为，给定一个任意的非负实数y{\displaystyle y}，我们能对y=x2{\displaystyle y=x^{2}}求解，得到x=± ± -->y{\displaystyle x=\pm {\sqrt {y}}}。

性质

函数f:X→ → -->Y{\displaystyle f:X\rightarrow Y}为一个满射，当且仅当存在一个函数g:Y→ → -->X{\displaystyle g:Y\rightarrow X}满足f∘ ∘ -->g{\displaystyle f\circ g}等于Y{\displaystyle Y}上的单位函数。（这个陈述等价于选择公理。）

根据定义，函数为双射当且仅当它既是满射也是单射。

如果f∘ ∘ -->g{\displaystyle f\circ g} 是满射，则f{\displaystyle f}是满射。

如果f{\displaystyle f}和g{\displaystyle g}皆为满射，则f∘ ∘ -->g{\displaystyle f\circ g}为满射。

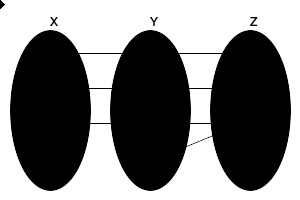
f:X→ → -->Y{\displaystyle f:X\rightarrow Y}为满射，当且仅当给定任意函数g,h:Y→ → -->Z{\displaystyle g,h:Y\rightarrow Z}满足g∘ ∘ -->f=h∘ ∘ -->f{\displaystyle g\circ f=h\circ f}，则g=h{\displaystyle g=h}。

如果f:X→ → -->Y{\displaystyle f:X\rightarrow Y}为满射，且B{\displaystyle B}是Y{\displaystyle 子集的子集，则，f(f− − -->1(B))=B{\displaystyle f(f^{-1}(B))=B}。因此，B{\displaystyle B}能被其原像复原。

任意函数h:X→ → -->Y{\displaystyle h:X\rightarrow Y}都可以分解为一个适当的满射f{\displaystyle f}和单射g{\displaystyle g}，使得h=g∘ ∘ -->f{\displaystyle h=g\circ f}。

如果f:X→ → -->Y{\displaystyle f:X\rightarrow Y}为满射函数，则X{\displaystyle X}在基数意义上至少有跟Y{\displaystyle Y}一样多的元素。

如果X{\displaystyle X}和Y{\displaystyle Y}皆为具有相同元素数的有限集合，则f:X→ → -->Y{\displaystyle f:X\rightarrow Y}是满射当且仅当f{\displaystyle f}是单射。

相关条目

单射

双射

参考文献

Bourbaki, Nicolas. Theory of Sets. Springer. 2004 [1968]. ISBN 978-3-540-22525-6. 

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。