定理

设Ω Ω -->{\displaystyle \Omega }是复平面C{\displaystyle \mathbb {C} }的一个单连通的开子集。f:Ω Ω -->→ → -->C{\displaystyle f\;:\;\;\Omega \;\rightarrow \mathbb {C} }是一个Ω Ω -->{\displaystyle \Omega }上的全纯函数。设γ γ -->{\displaystyle \gamma }是Ω Ω -->{\displaystyle \Omega }内的一个简单闭合的可求长曲线（即连续而不自交并且能定义长度的闭合曲线），那么函数f{\displaystyle f}在γ γ -->{\displaystyle \gamma }内部的点a{\displaystyle a}上的值是：

其中的积分为沿着γ γ -->{\displaystyle \gamma }逆时针方向的积分。

以上公式说明，全纯函数必然是无穷次可导的。这是因为假设以上的公式对函数f{\displaystyle f}的n阶导数成立：

对上式等号右侧的积分进行n次分部积分变换就可得到对n阶导数的柯西积分公式：

有时也称作柯西微分公式。右端是一个复可微的函数。这说明f{\displaystyle f}的n阶导数仍然是复可微的。所以依据数学归纳法可知f{\displaystyle f}是无穷次可导的，并且柯西微分公式对任意阶的导数都成立。

如果函数f{\displaystyle f}仅在γ γ -->{\displaystyle \gamma }内部是全纯函数，在边界γ γ -->{\displaystyle \gamma连续函数仅是连续函数，那么只有函数f{\displaystyle f}的柯西积分公式成立，而微分公式不一定成立。

证明

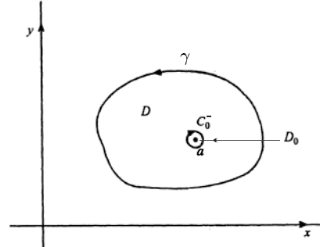
选定以a{\displaystyle a}为圆心，在γ γ -->{\displaystyle \gamma }内部的一个圆盘D0={z;|z− − -->a|⩽ ⩽ -->r}{\displaystyle D_{0}=\{z;\;|z-a|\leqslant r\}}，它的边界是圆C0={z;|z− − -->a|=r}{\displaystyle C_{0}=\{z;\;|z-a|=r\}}。函数fz− − -->a{\displaystyle {\frac {f}{z-a}}}在闭合区域D∖ ∖ -->D0{\displaystyle D\setminus D_{0}}上是全纯函数，所以根据柯西积分定理，它在边界上的积分等于0：

其中C0− − -->{\displaystyle C_{0}^{-}}的标记表示沿“内边界”C0{\displaystyle C_{0}}的积分是顺时针方向。所以将这个积分改为沿逆时针方向C0+{\displaystyle C_{0}^{+}}后，就能得到：

这个等式与圆盘D0{\displaystyle D_{0}}的半径r{\displaystyle r}无关，也就是说无论圆盘多幺小，这个等式都成立。注意到当半径r{\displaystyle r}趋于0的时候，函数f{\displaystyle f}在圆C0{\displaystyle C_{0}}上的值基本上等于f(a){\displaystyle f(a)}。所以

这说明

例子

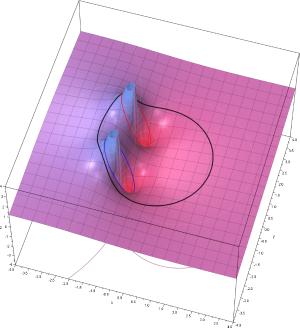
函数 g(z) = z / (z + 2z + 2) 实部的图像，在两个极点附近趋于无穷

考虑函数：g(z)=z2z2+2z+2{\displaystyle g(z)={\frac {z^{2}}{z^{2}+2z+2}}}以及闭合区域：|z| = 2。这是一个以原点为圆心，半径为2的圆，以下记作C{\displaystyle C}. 下面使用柯西积分公式计算g(z){\displaystyle g(z)}沿C{\displaystyle C}的积分。

首先，函数g{\displaystyle g}有两个极点，分别是方程z2+2z+2=0{\displaystyle z^{2}+2z+2=0}的两个复根：z1=− − -->1+i,{\displaystyle z_{1}=-1+i,}z2=− − -->1− − -->i.{\displaystyle z_{2}=-1-i.} 它们的模长都小于2，所以都在C{\displaystyle C}的内部。函数可以写成g{\displaystyle g}：

g{\displaystyle g}在两个极点附近趋于无穷。在两个极点周围各作一个小圆圈：C1{\displaystyle C_{1}}和C2{\displaystyle C_{2}}，应用柯西积分定理可知，所要求的积分

注意到函数f1=z2z− − -->z1{\displaystyle f_{1}={\frac {z^{2}}{z-z_{1}}}}在C2{\displaystyle C_{2}}内部是全纯函数，所以在C2{\displaystyle C_{2}}上的积分：

同理，函数f2=z2z− − -->z2{\displaystyle f_{2}={\frac {z^{2}}{z-z_{2}}}}在C1{\displaystyle C_{1}}内部是全纯函数，所以

所以

参见

柯西积分定理

刘维尔定理

留数定理

莫雷拉定理

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。