定义

电流密度 J 可以简单地定义为通过单位面积 A （国际单位：m ）的电流 I （国际单位：A）。它的量值由极限给出：

当电流密度作为矢量 J 时，在曲面 S 上进行曲面积分后，再对持续时间 t 1 到 t 2 积分，得到 ( t 2 − t 1 ) 这段时间流过该面的电荷总量：

计算通量所用到的面积可实可虚，可平可曲，可为截面也可为表面。例如，对于通过导体的载流子来说，这里遇到的面积是导体的截面。

重要性

对于电力系统和电子系统的设计而言，电流密度是很重要的。电路的性能与电流量紧密相关，而电流密度又是由导体的物体尺寸决定。例如，随着集成电路的尺寸越变越小，虽然较小的元件需要的电流也较小，为了要达到芯片内含的元件数量密度增高的目标，电流密度会趋向于增高。更详尽细节，请参阅摩尔定律。

在高频频域，由于趋肤效应，传导区域会更加局限于表面附近，因而促使电流密度增高。

电流密度过高会产生不理想后果。大多数电导体的电阻是有限的正值，会以热能的形式消散功率。为了要避免电导体因过热而被熔化或发生燃烧，并且防止绝缘材料遭到损坏，电流密度必须维持在过高值以下。假若电流密度过高，材料与材料之间的互连部分会开始移动，这现象称为电迁移（ electromigration ）。在超导体里，过高的电流密度会产生很强的磁场，这会使得超导体自发地丧失超导性质。

对于电流密度所做的分析和观察，可以用来探测固体内在的物理性质，包括金属、半导体、绝缘体等等。在这科学领域，材料学家已经研究发展出一套非常详尽的理论形式论，来解释很多机要的实验观察 。

安培力定律描述电流密度与磁场之间的关系。电流密度是安陪力定律的一个重要参数，

计算电流密度

自由电流

大自然有很多种载有电荷的粒子，称为“带电粒子”，例如，导电体内可移动的电子、电解液内的离子、等离子体内的电子和离子、强子内的夸克 。这些带电粒子的移动，形成了电流。电荷流动的分布可以由电流密度来描述：

其中， J ( r , t ) {\displaystyle \mathbf {J} (\mathbf {r} ,t)} 是在位置 r {\displaystyle \mathbf {r} } 、在时间 t {\displaystyle t} 的电流密度矢量， q {\displaystyle q} 是带电粒子的电荷量， n ( r , t ) {\displaystyle n(\mathbf {r} ,t)} 是带电粒子密度，是单位体积的带电粒子数量， ρ ρ --> ( r , t ) {\displaystyle \rho (\mathbf {r} ,t)} 是电荷密度， v d ( r , t ) {\displaystyle \mathbf {v} _{d}(\mathbf {r} ,t)} 是带电粒子的平均漂移速度。

电流密度时常可以近似为与电场成正比，以方程表达为

其中， E {\displaystyle \mathbf {E} } 是电场， J {\displaystyle \mathbf {J} } 是电流密度， σ σ --> {\displaystyle \sigma } 是电导率，是电倒数的倒数。

采用更基础性的方法来计算电流密度。这方法建立于方程

其中， r ′ {\displaystyle \mathbf {r} "} 和 t ′ {\displaystyle t"} 分别是位置积分变数和时间积分变数。

这方式显示出电导率 σ σ --> {\displaystyle \sigma } 在时间方面的滞后响应，和在空间方面的非局域响应属性。原则上，通过微观量子分析，才能推导出来电导率函数。例如，对于足够弱小的电场，可以从描述物质的电导性质的线性响应函数（ linear response function ）推导 。经过一番沉思，可以了解，这电导率和其伴随的电流密度反映出，在时间方面和在空间方面，电荷传输于介质的基本机制。

假设每当 Δ Δ --> t < 0 {\displaystyle \Delta t r ( Δ Δ --> t ) = 0 {\displaystyle \varepsilon _{r}(\Delta t)=0} ，则这积分的上限可以延伸至无穷大：

做一个对于时间与空间的傅里叶变换，根据折积定理，可以得到

其中， σ σ --> ( k , ω ω --> ) {\displaystyle \sigma (\mathbf {k} ,\omega )}波矢是参数为波矢 k {\displaystyle \mathbf {k} } 和角频率 ω ω --> {\displaystyle \omega } 的电导率复函数。

许多物质的电导率是张量，电流可能不会与施加的电场同方向。例如，晶体物质这是这样的物质。磁场的施加也可能会改变电导行为。

穿过曲面的电流

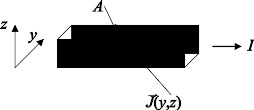
电流和电流密度之间的关系

穿过曲面 S {\displaystyle \mathbb {S} } 的电流 I {\displaystyle I} 可以用面积分计算为

其中， J {\displaystyle \mathbf {J} } 是电流密度， d a {\displaystyle \mathrm {d} \mathbf {a} } 是微小面元素。

连续方程

由于电荷守恒，从某设定体积流出的电流的净流量，等于在这体积内部的电荷量的净变率。以方程表达，

其中， ρ ρ --> {\displaystyle \rho } 是电荷密度， d r 3 {\displaystyle \mathrm {d} r^{3}} 是微小体元素， V {\displaystyle \mathbb {V} } 是闭曲面 S {\displaystyle \mathbb {S} } 所包围的体积。

这方程左边的面积分表示电流从闭曲面 S {\displaystyle \mathbb {S} } 所包围的体积 V {\displaystyle \mathbb {V} } 流出来，中间和右边的体积分的负号表示，随着时间的前进，体积内部的电荷量逐渐减少。

根据散度定理，

所以，

注意到对于任意体积 V {\displaystyle \mathbb {V} } ，上述方程都成立。所以，两个被积式恒等：

称这方程为连续方程 。

参阅

霍尔效应

量子霍尔效应

超导现象

漂移速度

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。