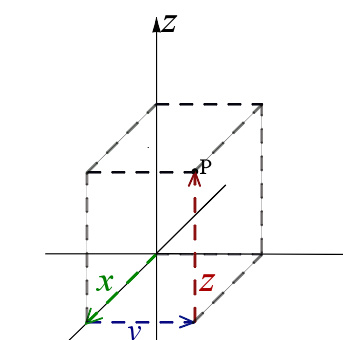
地平坐标系
简略的观测
地平坐标系统是固定在地球上而不是恒星,所以天体出现在天球上的高度和方位会随着时间,在天球上不停的改变。另一方面,因为基础平面是观测者所在地的地平面,所以相同的天体在相同的时间从不同的位置观察,也会有不同的高度和方位。
地平坐标系在测量天体的出没上非常的好用,当一个天体的高度为0°,就表示他位于地平线上。此时若其高度增加,就代表上升;若高度减少,便是下降。然而天球上所有天体的运动都受到由西向东的周日运动支配,所以与其笨拙的去观察高度是增加或减少,不如改为观察天体的方位更容易来判断是上升或是下降:
当天体的方位在0°~180°之间(北方—东方—南方,亦即子午线之东)是上升。
当天体的方位在180°~360°之间(南方—西方—北方,亦即子午线之西)是下降。
但在下面的特殊位置则例外:
在北极点,因为天顶就是北天极,所有的方向都是南方,所以无法定出方位,但这并不造成问题,因为所有天体的高度无论任何时间都不会改变,即既不升高也不降低,只绕北极星以 逆时针 转动。(头朝下感觉天星是顺时针转,抬头望天,才看见天星逆时针转)
在南极,地面上所有方向都是北方,也会有与北极相同情况,只是所有星星皆绕天顶的南天极 顺时针 转动。
在赤道,位于极点的天体会固定不动的永远停留在地平线上的那一个点。(但实际上由于天极很接近地平线,在该处天体未必能直接看到)
需要注意的是:前面所考虑的祇是理论上的 几何地平 ,即不考虑地球大气层对天体位置的影响,让观测者的地平线完全以理想的海平面构成。因为地球有弧度,实际上看见的 视地平面 会随着观测者的高度增加而降低(出现负值)。另一方面大气层也会将地平线下半度的天体折射到地平线上。
与赤道坐标系的互换
只要知道观测者的地理坐标与时间,就可以将地平坐标转换成赤道坐标,或是反过来将赤道坐标转换成地平坐标。(纬度在北极点是+90°,在赤道是0°,南极点是-90°。)
在数学公式中,以 A {\displaystyle A} 代表方位, a {\displaystyle a} 代表高度。
以 δ δ --> {\displaystyle \delta } 表示赤纬, H {\displaystyle H} 时角示时角。 φ为观测者所在地的纬度。
赤道坐标转为地平坐标
sin --> a = sin --> ϕ ϕ --> ⋅ ⋅ --> sin --> δ δ --> + cos --> ϕ ϕ --> ⋅ ⋅ --> cos --> δ δ --> ⋅ ⋅ --> cos --> H {\displaystyle \sin a=\sin \phi \cdot \sin \delta +\cos \phi \cdot \cos \delta \cdot \cos H}
cos --> A ⋅ ⋅ --> cos --> a = cos --> ϕ ϕ --> ⋅ ⋅ --> sin --> δ δ --> − − --> sin --> ϕ ϕ --> ⋅ ⋅ --> cos --> δ δ --> ⋅ ⋅ --> cos --> H {\displaystyle \cos A\cdot \cos a=\cos \phi \cdot \sin \delta -\sin \phi \cdot \cos \delta \cdot \cos H}
sin --> A ⋅ ⋅ --> cos --> a = − − --> cos --> δ δ --> ⋅ ⋅ --> sin --> H {\displaystyle \sin A\cdot \cos a=-\cos \delta \cdot \sin H}
有些人或许会试图将最后两个公式相除来加以简化,以消除 cos --> a {\displaystyle \cos a} ,而只剩下 tan --> A {\displaystyle \tan A} 。但是正切函数不能清楚的区别出象限,例如45°和225°是完全不同的方位,分别指向相对的东北方和西南方。像这种情况,就必须要事先知道方位角象限的方位角才是需要的方位。如果计算的工作是使用口袋型计算机来执行,那么如果可能的话,最好要避免使用正弦和余弦的反函数,因为他们的极限范围只有180°,而且在±90°与0°和180°的附近精确度很低。好在大部分的工程用计算机都能将直角坐标转换成极坐标(R->P)和将极坐标转换成直角坐标(R->P),可以避开这些问题和提供验算的功能。
算法将成为下面的形式:
将上面三个公式在等号右边的项目做转换
运用R→P转换将 cos --> A ⋅ ⋅ --> cos --> a {\displaystyle \cos A\cdot \cos a} 成为X值, sin --> A ⋅ ⋅ --> cos --> a {\displaystyle \sin A\cdot \cos a} 成为Y值
答案中角度的部分是方位角,范围是完整的0°至360°(或-180°至+180°)
再度使用R→P转换将最后答案中的径度量转换成X值,并将 sin --> a {\displaystyle \sin a} 转换成第一个公式的Y值。
答案中角度的部分是高度,范围在-90°至+90°之间。
径度量的数值必须正好是1,否则你的计算一定是错了!
地平坐标转为赤道坐标
地平坐标也可以转换成赤道坐标:
sin --> δ δ --> = sin --> ϕ ϕ --> ⋅ ⋅ --> sin --> a + cos --> ϕ ϕ --> ⋅ ⋅ --> cos --> a ⋅ ⋅ --> cos --> A {\displaystyle \sin \delta =\sin \phi \cdot \sin a+\cos \phi \cdot \cos a\cdot \cos A}
cos --> δ δ --> ⋅ ⋅ --> cos --> H = cos --> ϕ ϕ --> ⋅ ⋅ --> sin --> a − − --> sin --> ϕ ϕ --> ⋅ ⋅ --> cos --> a ⋅ ⋅ --> cos --> A {\displaystyle \cos \delta \cdot \cos H=\cos \phi \cdot \sin a-\sin \phi \cdot \cos a\cdot \cos A}
cos --> δ δ --> ⋅ ⋅ --> sin --> H = − − --> sin --> A ⋅ ⋅ --> cos --> a {\displaystyle \cos \delta \cdot \sin H=-\sin A\cdot \cos a}
同样的,在演算时也要尽量避免使用正弦和余弦的反函数。
太阳的位置
在地平坐标系统中,有好几种方法可以计算太阳的视位置。
完整和精确的计算方法可以参考比利时天文学家简米斯的天文计算(Astronomical Algorithms)
下面是一种简单的近似计算法的例子:
已知:
在一年中的日期和当天的时间
观测者的地理坐标(经度、纬度)和时区
你需要进行下面的计算,以下面的公式可以算出太阳的赤纬:
δ δ --> = − − --> 23.45 ∘ ∘ --> ⋅ ⋅ --> cos --> ( 360 ∘ ∘ --> 365 ⋅ ⋅ --> ( N + 10 ) ) {\displaystyle \delta =-23.45^{\circ }\cdot \cos \left({\frac {360^{\circ }}{365}}\cdot \left(N+10\right)\right)}
此处的 N {\displaystyle N} 是自1月1日开始的天数。
此处的真时角是观测者因为地球的自转与太阳之间相对应的角度。
由于 T {\displaystyle T} 是以时来计算,而地球每小时转动15度,所以 H {\displaystyle H} 的单位是度。如果要转成径度量,只要成上2π/360就可以了。
使用地平坐标系统中的公式计算太阳的高度与方位:
这篇文章最早出现在贾森・哈里斯附在KStars的附录中。适合Linuxc和KDE的天象仪程式,可以拜访后附的网址:tml
免责声明:以上内容版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。感谢每一位辛勤著写的作者,感谢每一位的分享。

- 有价值
- 一般般
- 没价值








24小时热门
推荐阅读


知识互答
关于我们

APP下载
























{{item.time}} {{item.replyListShow ? '收起' : '展开'}}评论 {{curReplyId == item.id ? '取消回复' : '回复'}}