



态矢量
性质1)共轭复数|ββ-->⟩⟩-->{displaystyle|betarangle,!}内积|αα-->⟩⟩-->{displaystyle|alphara
性质
1)共轭复数
| β β --> ⟩ ⟩ --> {\displaystyle |\beta \rangle \,\!} 内积 | α α --> ⟩ ⟩ --> {\displaystyle |\alpha \rangle \,\!} 是 | α α --> ⟩ ⟩ --> {\displaystyle |\alpha \rangle \,\!} 内积 | β β --> ⟩ ⟩ --> {\displaystyle共轭复数eta \rangle \,\!} 的共轭复数:
2)归一性
定义 | α α --> ⟩ ⟩ --> {\displaystyle |\alpha \rangle \,\!} 内积 | α α --> ⟩ ⟩ --> {\displaystyle |\alpha \ran平方根 \,\!} 的平方根为 | α α --> ⟩ ⟩ --> {\displaystyle |\alpha \rangle \,\!} 的范数,标记为 | α α --> | {\displaystyle |\alpha |\,\!} 。由于态矢量满足归一性,态矢量的范数必定等于1:
3)柯西-施瓦茨不等式
柯西-施瓦茨不等式阐明:
参考文献
费曼, 理查; 雷顿, 罗伯; 山德士, 马修. 费曼物理学讲义III (2)量子力学应用. 天下文化书. 2006: pp. 10–17. ISBN 986-417-672-2. 引文格式1维护:冗余文本 (link)
免责声明:以上内容版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。感谢每一位辛勤著写的作者,感谢每一位的分享。
——— 没有了 ———
编辑:阿族小谱

文章价值打分
- 有价值
- 一般般
- 没价值
当前文章打 0 分,共有 0 人打分
文章观点支持

0

0
文章很值,打赏犒劳一下作者~

发表评论
写好了,提交
{{item.label}}
{{commentTotal}}条评论
{{item.userName}}
发布时间:{{item.time}}
{{item.content}}
回复
举报


打赏作者
“感谢您的打赏,我会更努力的创作”
— 请选择您要打赏的金额 —
{{item.label}}


{{item.label}}

打赏成功!
“感谢您的打赏,我会更努力的创作”
返回
打赏
私信
推荐阅读
· 赝矢量
物理例子物理中赝矢量的例子包括有磁场、力矩、涡量及角动量。一部要远离的车,各轮子对一观察者产生的角动量为向右的,这部车产生的镜像,各轮子对同一观察者产生的角动量也是向右的考虑赝矢量角动量L=r×p。假设开一部车前进,各轮子产生的角动量会朝左。若考虑车子的镜像,角动量矢量若以一般矢量的观点来看,其镜像应该往右,但真正车子镜像的角动量仍然往左(在镜像中的车轮仍然往前进),因此在赝矢量反射后,会比一般矢量多一个负号。矢量和赝矢量之间的不同在研究物理系统的对称性时很重要。考虑在一个z=0平面上的线圈,上面有电流,会产生一个z方向的磁场,此系统在z平面的镜相反射下是对称(不变)的,磁场不会因镜相反射而相反,但是若将磁场视为一个一般的矢量,应该会随镜相反射而相反,其原因就是因为磁场是赝矢量,产生一个额外的负号,因为没有反相。相关条目外代数克利福德代数定向(数学)可定向性赝标量赝张量
· 保守矢量场
定义一个矢量场v{\displaystyle\mathbf{v}}称为保守的,如果存在一个标量场φφ-->{\displaystyle\varphi},使得:在这里,∇∇-->φφ-->{\displaystyle\nabla\varphi}表示φφ-->{\displaystyle\梯度rphi}的梯度。当以上的等式成立时,φφ-->{\displaystyle\varphi}就称为v{\displaystyle\mat标量势{v}}的一个标量势。矢量分析基本定理表明,任何一个矢量场都可以表示为一个保守矢量场和一个螺线矢量场的和。路径无关保守矢量场的一个重要性质是它沿着一条路径的积分只与起点和终点有关,与路径无关。假设S⊆⊆-->R3{\displaystyleS\subseteq\mathbb{R}^{3}}是三维空间内的一个区域,P{\displa...
· 坡印亭矢量
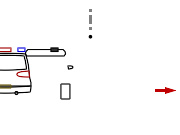
定义在坡印亭的原始论文和许多教科书中,它通常记作S或N,定义为其中E是电场强度;H是磁场强度。这种形式通常被称为亚伯拉罕形式。偶尔也用电场强度E和磁感应强度B作为另一种定义。甚至可以把电位移矢量D和磁感应强度B结合起来得到的坡印亭矢量的闵可夫斯基形式,或使用D与H构成另一种形式。选用哪种形式一直是有争议的:罗伯特·费福(RobertPfeifer)等人总结并一定程度上解决了亚伯拉罕与闵可夫斯基形式支持者之间长达一个世纪的争议。坡印亭矢量表示的是电磁能量的能流矢量的特殊情况。然而,空间内任何形式的能量都有其移动方向,也有密度,所以其他形式的能量也可以定义能流矢量,例如机械能。1874年由尼科莱·乌诺夫发现的乌诺夫–坡印亭矢量以完全广义的观点描述了液体和弹性介质中的能流。说明一个由电池(V)和电阻(R)组成的直流电路,用(S,蓝)表示在周围空间中的坡印亭矢量的方向,产生其的电场为(E,红),磁...
· 螺线矢量场
例子磁场B是螺线矢量场(参见麦克斯韦方程组);不可压缩流体的速度场是螺线矢量场。
· 矢量图形

综述所有的现代计算机显示器都要将矢量图形转换成栅格图像的格式,包含屏幕上每个像素数值的栅格图像保存在内存中。从计算机发展的最初1950年代一直到1980年代,曾经使用过一种不同类型的矢量图形系统显示器。在这些系统中CRT显示器的电子束直接逐段生成所需图形,屏幕其它部分保持为黑的状态。为了达到没有闪烁或者接近没有闪烁的效果,这个过程每秒要重复很多次。这种显示系统可以生成分辨率非常高的艺术线条,并且不需要栅格系统生成同样分辨率所需要的对于当时来说非常巨大的内存空间。这种基于矢量的显示器称为X-Y显示器。矢量化是去除照片中多余信息的好方法。(为了在本页显示,图像转成了JPEG格式。)原始照片,JPEG栅格图像矢量化的SteamLocomotive7646,最初是WindowsMetafile格式。矢量图形显示器的最初应用之一是USSAGE防空系统。矢量图形系统只有在1999年美国的空管中出现过故
关于我们

关注族谱网 微信公众号,每日及时查看相关推荐,订阅互动等。
APP下载

下载族谱APP 微信公众号,每日及时查看

扫一扫添加客服微信
















