恒星结构-族谱新闻-族谱网

恒星结构

2020-10-16

出处：族谱网

作者：阿族小谱

浏览:721次

转发:0次

评论:0

能量转移这张图显示太阳质量主序星的剖面结构。NASA的图像恒星以不同的方法将不同的层次的热量向上层并向外转移，主要是以对流和辐射转移，但是在白矮星热传导却非常重要。在温度梯度足够时，对流是能量转移的主导方式，气体在一个特定的小包内，如果经由绝热过程轻微的上升，它便会在恒星内持续的上升。在这种情况下，如果它比周围的环境稍为温暖一些，上升中的小包是有浮力的，并且会继续上升；如果上升中的小包比周围的气体冷，它将会落回它原来的高度。在温度梯度较低和透明度低的区域，能量将通过辐射来转移，而辐射成为能量转移的主导。主序星内部的结构取决于恒星的质量。质量与太阳相近的恒星(0.3–1.5太阳质量)，包括太阳，不需要太大的温度梯度，氢转换成氦的融合主要通过质子-质子链进行。因此，内部的能量转移辐射为主导。质量与太阳相近的恒星，在外围的部分温度够低，因此氢呈现中性，对紫外光是不透明的，所以对流成为主导。因此，...

能量转移

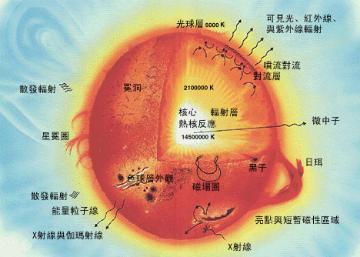
这张图显示太阳质量主序星的剖面结构。 NASA的图像

恒星以不同的方法将不同的层次的热量向上层并向外转移，主要是以对流和辐射转移，但是在白矮星热传导却非常重要。

在温度梯度足够时，对流是能量转移的主导方式，气体在一个特定的小包内，如果经由绝热过程轻微的上升，它便会在恒星内持续的上升。在这种情况下，如果它比周围的环境稍为温暖一些，上升中的小包是有浮力的，并且会继续上升；如果上升中的小包比周围的气体冷，它将会落回它原来的高度。在温度梯度较低和透明度低的区域，能量将通过辐射来转移，而辐射成为能量转移的主导。

主序星内部的结构取决于恒星的质量。

质量与太阳相近的恒星(0.3–1.5太阳质量)，包括太阳，不需要太大的温度梯度，氢转换成氦的融合主要通过质子-质子链进行。因此，内部的能量转移辐射为主导。质量与太阳相近的恒星，在外围的部分温度够低，因此氢呈现中性，对紫外光是不透明的，所以对流成为主导。因此，质量与太阳相近的恒星有着辐射的核心，在外围则是对流的壳层。

质量稍大的恒星(质量大于1.5太阳质量)，核心的温度大约超过 1.8 × × --> 10 7 {\displaystyle 1.8\times 10^{7}} K，所以氢融合成氦的过程主要是碳氮氧循环。在碳氮氧循环，能量孳生率是温度的15次方，而质子-质子链的孳生率只是温度的4次方。由于碳氮氧循环对温度的高度敏感，在恒星内部的温度梯度已经足以在核心造成对流。在恒星的外围部分，温度梯度更低，但温度足够高到使得氢几乎完全都被电离，所以恒星仍然以紫外线的形式辐射出能量。所以大质量的恒星外面是辐射的壳层。

载主序带上值量最低的恒星没有辐射层，主导能量传输的机制是对流。巨星也几乎全都是对流。

恒星结构方程式

最简单和最常用的恒星结构模型是球状对称的准静态模型，假设恒星是处在稳定状态并且是球型对称，它包含4个基本的一阶偏微分方程：两个用来描述物质和压力随着半径的变化；另外两个用来描述温度与光度随着半径的变化。。

在组成的恒星结构方程式 (利用假设的球状对称)中，要考虑的各项是物质密度 ρ ρ --> ( r ) {\displaystyle \rho (r)} 、温度 T ( r ) {\displaystyle T(r)} 、总压力(气体的热压力加上辐射压) P ( r ) {\displaystyle P(r)} 、光度 l ( r ) {\displaystyle l(r)} ，和在距离中心 r {\displaystyle r} ，厚度 d r {\displaystyle {\mbox{d}}r} 的球壳，每单位质量的能量孳生率 ϵ ϵ --> ( r ) {\displaystyle \epsilon (r)} 。这颗恒星被假设局部热力平衡(LTE)，所以物质和光子的温度相等的。虽然局部热力平衡不是严格的被遵守，因为对指定的壳层之下的温度永远比上面的高，良好的近似范围可以估计自由子的平均自由径 λ λ --> {\displaystyle \lambda } ，因为这个长度远比考虑的温度变化为小，也就是说 λ λ --> ≪ ≪ --> T / | ∇ ∇ --> T | {\displaystyle \lambda \ll T/|\nabla T|} 。

第一种状态是流体静力平衡：恒星内部向外的力量来自压力梯度与来自万有引力向内的力量完全平衡。

此处 m ( r ) {\displaystyle m(r)} 是在壳层 r {\displaystyle r} 内部累积的总质量， G 是万有引力常数。累积的总质量依据质量连续方程式随着距离的增加而增加：

质量连续方程式的积分由恒心中心( r = 0 {\displaystyle r=0} ) 至恒星半径为( r = R {\displaystyle r=R} ) 之处时，就可以得到恒星的总质量。

考虑能量从球壳向外传送的是能量方程式：

此处 ϵ ϵ --> ν ν --> {\displaystyle \epsilon _{\nu }} 是单位质量以微中子的形式产生的光度(通常不会与一般的物质产生交互作用而逃离恒星)。在恒星的核心之外，核反应不会发生，也就是没有能量产生，因此发光度是一个常数。

能量转移方程式决于能量转移的模型而有不同的形式。以传导性的光度转移(适用于白矮星)，能量方程式是：

此处 k 是导热率。

在能量以辐射传送的情况下，这适用于主序带上与太阳类似，核心外有壳层包围着的大质量主序星的恒星内部：

此处 κ κ --> {\displaystyle \kappa } 是物质的不透明性， σ σ --> {\displaystyle \sigm斯特凡是斯特凡-波兹曼常数，并且波兹曼常数被设定为1。

在能量以对流传送的情况下(适用于所有主序带上没有辐射部分的巨星和低质量恒星)，已知可用数学公式还没有一个是严谨的。对流的能量传送通常都使用混合长度理论，混合长度理论对恒星气体的处理是认为分离的各种不同元素，保留了周围的温度、密度和压力，但是在恒星内能移动的距离就是特征长度，称为混合长度。对单原子理想气体，混合长度理论认为：

此处 γ γ --> = c p / c v {\displaystyle \gamma =c_{p}/c_{v}} 是绝热指数，在气体就是比热的比率(对完全电离的理想气体， γ γ --> = 5 / 3 {\displaystyle \gamma =5/3} .)。

还需要状态方程式，关系到其他区域的压力变化，适用于材料，像是温度、密度、化学组成等等。相关的状态也许必须包括理想气体定律、辐射压、来自电子简并的压力等等。

与一系列的边界条件组合，这些方程式的一个解可以完整的叙述恒星的行为。典型的边界条件设由观测的参数来设定数值，适当的恒星表面( r = R {\displaystyle r=R} )和中心( r = 0 {\displaystyle r=0} )： P ( R ) = 0 {\displaystyle P(R)=0} ，意思是恒星表面的压力为0； m ( 0 ) = 0 {\displaystyle m(0)=0} 为在恒星的中心没有质量；如同必须假设密度是有限的， m ( R ) = M {\displaystyle m(R)=M} 就是恒星的总质量；而 T ( R ) = T e f f {\displaystyle T(R)=T_{eff}} 是恒星表面的有效温度。

虽然现在的恒星演化模型能描述赫罗图的主要特征，重要的改进已经能将与我们再传送现象的知识及现下仍不确定的因素移除，但最困难的挑战依然是扰动的数值作业。一些研究小组正在开发的模型可以演算在三度空间的简易扰动。