常见定义

对于一维实随机变量 X ，设它的累积分布函数是 F X ( x ) {\displaystyle F_{X}(x)} 。如果存在可测函数 f X ( x ) {\displaystyle f_{X}(x)} ，满足：

那么 X 是一个连续型随机变量，并且 f X ( x ) {\displaystyle f_{X}(x)} 是它的概率密度函数。

性质

连续型随机变量的概率密度函数有如下性质：

∀ ∀ --> − − --> ∞ ∞ --> < x , f X ( x ) ≥ ≥ --> 0 {\displaystyle \forall -\infty

∫ ∫ --> − − --> ∞ ∞ --> ∞ ∞ --> f X ( x ) d x = 1 {\displaystyle \int _{-\infty }^{\infty }f_{X}(x)\,dx=1}

∀ ∀ --> − − --> ∞ ∞ --> < a < b , P [ a b ] = F X ( b ) − − --> F X ( a ) = ∫ ∫ --> a b f X ( x ) d x {\displaystyle \forall -\infty

如果概率密度函数 f X ( x ) {\displaystyle f_{X}(x)} 在一点 x {\displaystyle x} 上连续，那么累积分布函数可导，并且它的导数： F X ′ ′ --> ( x ) = f X ( x ) {\displaystyle F_{X}^{\prime }(x)=f_{X}(x)}

由于随机变量 X 的取值 P [ a b ] {\displaystyle \mathbb {P} \left[a 只取决于概率密度函数的积分，所以概率密度函数在个别点上的取值并不会影响随机变量的表现。更准确来说，如果一个函数和 X 的概率密度函数取值不同的点只有有限个、可数无限个或者相对于整个实数轴来说测度为0（是一个零测集），那么这个函数也可以是 X 的概率密度函数。

连续型的随机变量取值在任意一点的概率都是0。作为推论，连续型随机变量在区间上取值的概率与这个区间是开区间还是闭区间无关。要注意的是，概率

但 { X = a } {\displaystyle \{X=a\}} 并不是不可能事件。

例子

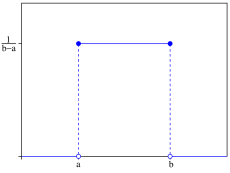
连续型均匀分布的概率密度函数

最简单的概率密度函数是均匀分布的密度函数。对于一个取值在区间 [ a , b ] {\displaystyle [a,b]} 上的均匀分布函数 I [ a , b ] {\displaystyle \mathbf {I} _{[a,b]}} ，它的概率密度函数：

也就是说，当 x 不在区间 [ a , b ] {\displaystyle [a,b]} 上的时候，函数值等于0，而在区间 [ a , b ] {\displaystyle [a,b]} 上的时候，函数值等于 1 b − − --> a {\displaystyle \scriptstyle {\frac {1}{b-a}}} 。这个函数并不是连续函数续函数，但是是可积函数。

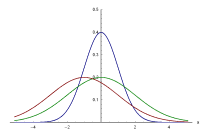
正态分布的概率密度函数

正态分布是重要的概率分布。它的概率密度函数是：

随着参数 μ μ --> {\displaystyle \mu } 和 σ σ --> {\displaystyle \sigma } 变化，概率分布也产生变化。

应用

随机变量X的n阶矩是X的n次方的期望值，即

X的方差为

更广泛的说，设 g {\displaystyle g} 为一个有界连续函数，那么随机变量 g ( X ) {\displaystyle g(X)} 的数学期望

特征函数

对概率密度函数作类似傅利叶变换可得特征函数。

特征函数与概率密度函数有一对一的关系。因此，知道一个分布的特征函数就等同于知道一个分布的概率密度函数。

参考文献

书籍

钟开莱. 《概率论教程》. 上海科学技术出版社. 1989. ISBN 7-5323-0648-8.

参见

概率分布

概率质量函数

累积分布函数

条件概率密度函数

似然函数

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。