基本特性

图为一K介子（ K + ）变成三个π介子（2 π + ， 1 π − ）的衰变，这过程涉及了弱与强相互作用。 弱相互作用：K介子内的奇夸克（ s ）衰变成一反上夸克（ u ），并发射一W + 玻色子；随后 W + 玻色子衰变成一反下夸克（ d ）及一上夸克（ u ）。 强相互作用：一上夸克（ u ）发射出一胶子（ g ），该胶子随后衰变成一下夸克（ d ）及一反下夸克（ d ）。

四种K介子分别为：

带负电的 K − （含有一个奇夸克及一个反上夸克），质量为 493.667 ± 0.013 MeV ，平均寿命为 1.2384 ± 0.0024 × 10 s 。

其反粒子，带正电的 K + （含有一个上夸克及一个反奇夸克）的质量及寿命必须等同于 K − （由于CPT对称的关系）。两者质量差为 0.032 ± 0.090 MeV ，跟零一致。而寿命差则为 0.11 ± 0.09 × 10 s 。

中性（不带电荷）的 K 0 （含有一个下夸克及一个反奇夸克），其质量为 497.648 ± 0.022 MeV 。其均方电荷半径为 −0.076 ± 0.01fm 2 。

K 0 的反粒子为 K 0 （含有一个奇夸克及一个反下夸克），两者质量一致。

从夸克模型分配可轻易看出，K介子组成两组同位旋双重态；也就是说它们属于SU(2)基础表示的 2 。奇异数为+1的一组包括 K + 及 K 0 。而它们的反粒子组成另一组双重态（奇异数为-1）。

^强本征态。没有确切的寿命。 ^弱本征态。构成内没有小ε的CP破坏项。 ^ K 0 L 及 K 0 S 的质量于上表上与 K 0 无异。然而，已知 K 0 L 及 K 0 S 的质量有异，差异的大小尺度为 3.5 × 10 MeV/ c 。 ^ 由于中性粒子混合的关系，所以 K 0 L 及 K 0 S 并非奇异数的本征态。

衰变

中性K介子

尽管 K 0 及其反粒子 K 0 经由强相互作用产生，但是它们经由弱相互作用衰变。因此，在诞生后它们较适合被视为两个有着相当不同寿命的弱本征态：

长命的K介子被称为 K L （K-long，长命K），主要衰变成三个π介子，其平均寿命为 5.18 × 10 s 。

短命的K介子被称为 K S （K-short，短命K），主要衰变成两个π介子，其平均寿命为 8.958 × 10 s 。

（见下文的中性K介子混合）

虽然其他中性味的介子也有近似的混合情况，但是只有K介子的两种弱本征态被视为两种粒子，因为它们两者的寿命差异实在很大 。

1964年一实验发现长命K很少会衰变成两个π介子，这正是发现CP破坏的关键之一（见下文）。

带电荷K介子

K + 的主要衰变模式为：

奇异数

在1947年，曼彻斯特大学 G·D·罗彻斯特 （ 英语 ： George Rochester ） 和 克里福德·查理斯·巴特勒 （ 英语 ： Clifford Charles Butler ） 发表了两辐宇宙线引发反应的云室照片，一辐看起来是一中性粒子衰变成两个带电荷的π介子，另一辐看起来是一带荷的粒子衰变成一带电荷的π介子及一些中性的东西。新粒子的质量估算相当粗略，约为质子质量的一半。之后这种“V粒子”的个案就慢慢地涌现。

加州理工学院取得最早的突破，他们为了得到更佳的宇宙线接收，而把云室运上了威尔逊山。在1950年，他们报告了30个带电荷及4个中性的V粒子。受这个所启发，往后几年的很多观测都在山顶上进行，而1953年之前，所用的词汇如下：“L介子”指的是μ子或π介子。“K介子”指的是质量介乎π介子及核子间的粒子；而“超子”指的质量比核子大的粒子。

K介子与超子的衰变非常慢；一般大小尺度为 10 s 。然而，在π介子－质子反应所生产出的这些粒子的衰变则要快得多，时间大小尺度为 10 s 。这个不协调问题由亚伯拉罕·派斯所解决，他设定了一个新的量子数的叫奇异数，在强相互作用下守恒，但在弱相互作用下则不守恒。由于奇夸克及其反粒子一起的“相伴产生”，所以出现很大量的奇异粒子。奇异数很快就被指出它不是一个乘法量子数，因为如果是的话，奇异数会允许一些未被当时新的同步加速器所观测到的反应；布鲁克哈芬国家实验室在1953年，劳伦斯伯克利国家实验室在1955年被委托制作同步加速器。

宇称不守恒

带电荷的奇介子有两种衰变模式：

由于两种衰变的终态具有不同的宇称，所以科学家们认为两种初态应该为不同种类的粒子，因此是两种有区别的粒子。但是，在愈来愈准确的测量下，都没有发现两者之间的质量与寿命有什么差别，由此显示它们是同一种粒子。这个问题被称为 τ－Θ问题 。直到发现弱相互作用的宇称不守恒才被解决。由于介子通过弱相互作用衰变，宇称并不需要守恒，因此两种衰变可能由同一种粒子引起，也就是现在的 K + 。

中性介子振荡中的CP破坏

尽管宇称不守恒，电荷－宇称对称在一开始时是被认为是守恒的。要明白CP破坏的发现，就必须明白中性K介子的混合；这个现象的发生并不需要CP破坏，但是就是在这个背景下第一次测量到CP破坏。

中性K介子混合

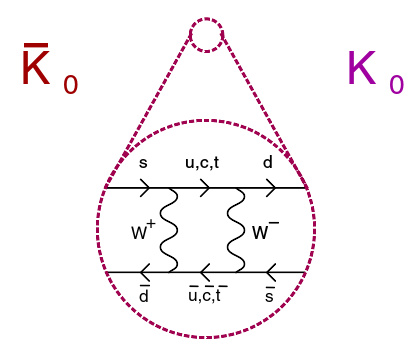
两种不同的中性K介子，有着不同的奇异数，但就可以通过弱相互作用来互相变换，这是因为弱相互作作用并不守恒奇异数。 K 0 内的奇夸克变成一下夸克，接着放射出两个相反电荷的W玻色子。 K 0 内的反下夸克则通过吸收W玻色子而变成一奇夸克。

由于中性K介子带有奇异数，它们不能互为对方的反粒子。所以一定有两种不同的K介子，两者奇异数的差为两个单位。问题是如何得知这两种介子的存在。而答案用到一种现象叫 中性粒子振荡 ，在这种现象中两种介子会通过弱相互作用互相变换，过种中弱相互作用会导致它们衰变成π介子（见右图）。

这些振荡最早由默里·盖尔曼与亚伯拉罕·派斯共同研究。他们研究过相反奇异数态在CP不变下随时间的演化。用矩阵形式写法如下

其中ψ为系统的量子态，由两个基态（在时间t=0时为a及b）的波辐共同决定。哈密顿矩阵对角线上的元（ M ）是守恒奇异数的强相互作用物理所引起的后果。两个对角线元必须相等，因为在没有弱相互作用的情况下，粒子与其反粒子的质量相等。不在对角线上的元（Δ），负责混合相反的奇异粒子，它们是由弱相互作用所引起的；CP对称要求它们全部都是实数。

矩阵 H 为实数的后果是，这两种态的概率会永恒地来回振荡。然而，假若矩阵的任何部分为虚数，就像CP对称所禁止的那样，那么整个组合的一部分会随时间而缩减。缩减的部分可以是一个分量(a)或另一个(b)，或是两者的混合。

混合

把矩阵对角化后可得本征态。这样会产生新的本征矢量，我们可以把它叫做 K 1 ，它是两相反奇异数态的总和，而 K 2 则是两态间的差。 K 1 及 K 2 为 CP 的本征态，两者有着相反的本征量； K 1 的 CP 为+1，而 K 2 则为-1。由于二π介子系统的 CP 也是+1，所以 K 1 可以这样衰变。而 K 2 则必须衰变成三个π介子。由于 K 2 的质量只比三个π介子加起来大一点点，所以衰变过程非常缓慢，大概比 K 1 衰变成两个π介子慢600倍。这两种不同的衰变模式由利昂·莱德曼及其同事于1956年观测到，并确立了中性K介子两个弱本徴态（在弱相互作用下，有着特定衰变寿命的态）的存在。

这两个弱本征态被称为 K L （长命K）及 K S （短命K）。在假定CP对称的情况下， K S = K ， K L = K 。

振荡

一初态为 K 0 的粒子束，会在传播时变成自己的反粒子，而反粒子又会变回原来的粒子，如此类推。这就是粒子振荡。在观测弱相互作用衰变成轻子时，发现 K 0 总是衰变成电子，而反粒子 K 0 则总是衰变成正电子。前文的分析提到纯 K 0 及反粒子 K 0 的粒子源，与电子与正电子生产率的关系。分析这种半轻子衰变的时间演化，可以发现有振荡现象，并且能够得悉 K S 及 K L 间的质谱分裂。由于这是由弱相互作用引起的，质谱分裂非常小，约为每一态质量的10 倍。

再生

一东中性K介子在飞行中衰变，因此短命的 K S 就此消失，剩下一束纯 K L 。假设这束粒子被射进物质里，那么 K 0 及其反粒子 K 0 就会与原子核有着不同的相互作用。 K 0 与核子产生准弹性散射，而反粒子 K 0 则有可能产生超子。由于两个部分与核子有着不同的相互作用，两粒子间失去了原有的量子同调。 不久之后，罗伯特·艾德尔与同事们报告 K S 的再生比预期多，就此开启了历史的新篇章。

CP破坏

在核实艾德尔的结果时，布鲁克哈芬国家实验室的詹姆斯·克罗宁与瓦尔·菲奇于1964年发现 K L 衰变成两个π介子（ CP =+1）。根据前文的解释，要上述衰变成立，就必须假设初态及终态的 CP 值不一样，因此他们马上提出了CP破坏。其他解释，例如非线性量子物理及未被观测到的新粒子，在不久后就被排除，剩下的CP破坏就是唯一的可能性。克罗宁与菲奇因这个发现而于1980年了荣获诺贝尔物理学奖。

事实上，尽管 K L 及 K S 为弱本征态（因为它们有各自不变的衰变平均寿命，而衰变就是由弱相互作用所引起的），但是它们并不太是 CP 本征态。取而代之的是，在ε很小的情况下（在一个重整化以内），

而 K S 也是相近的情况。因此有些时候 K L 衰变时 CP =+1，而同样地 K S 可以有 CP =-1的衰变。这就是 间接CP破坏 ，由 K 0 及其反粒子混合所造成的CP破坏。同时有一种 直接CP破坏 ，也就是在衰变过程当中的P破坏。因为混合与衰变都是由W玻色子的同一种相互作用所造成，所以存在两种CP破坏，也是因为这样才会有CKM矩阵所预测的CP破坏。

另见

强子、介子、超子及味

奇夸克及夸克模型

宇称、电荷共轭、时间反转对称、CPT对称及CP破坏

中微子振荡

注释及参考来源

参考文献

C.Amsler; Doser, M; Antonelli, M; Asner, D; Babu, K; Baer, H; Band, H; Barnett, R; Bergren, E; 等. Review of Particle Physics.Physics Letters B(Particle Data Group). 2008, 667 (1): 1–1340.Bibcode:2008PhLB..667....1P. doi:10.1016/j.physletb.2008.07.018 . 引文格式1维护：显式使用等标签 (link)

S. Eidelman; 等.Review of Particle Physics 2004 – Strange Mesons. Particle Data Group. 2004. 引文格式1维护：显式使用等标签 (link)

The quark model , by J.J.J. Kokkedee

M.S. Sozzi. Discrete symmetries and CP violation.Oxford University Press. 2008. ISBN 978-0-19-929666-8.

I.I. Bigi, A.I. Sanda. CP violation.Cambridge University Press. 2000. ISBN 0-521-44349-0.

D.J. Griffiths. Introduction to Elementary Particle. John Wiley & Sons. 1987. ISBN 0-471-60386-4.

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。