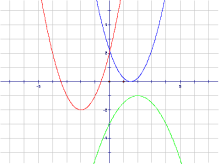
二次方程
一元二次方程
表达式
一元二次方程是指只含有一个未知数的二次方程,它的基本表达式为: a x 2 + b x + c = 0 {\displaystyle ax^{2}+bx+c=0\,} 其中 ( a ≠ ≠ --> 0 ) {\displaystyle (a\neq 0)} 。 a {\displaystyle a\,} 为方程的系数项系数, b {\displaystyle b\,} 为一次项系数, c {\displaystyle c\,}常数为常数。若 a = 0 {\displaystyle a=0\,} ,则该方程没有二次项,即变为一次方程。
判别式
■ ⁄ 2 x + ⁄ 2 x − ⁄ 3 ■ − ⁄ 3 x + ⁄ 3 x − ⁄ 3 ■ x + ⁄ 2
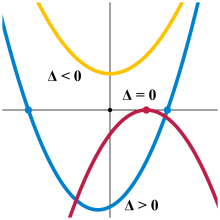
Δ Δ --> = b 2 − − --> 4 a c {\displaystyle \Delta =b^{2}-4ac\,}
方程的根和判别式的关系
若 Δ Δ --> > 0 {\displaystyle \Delta >0\,} ,该实数有两个不相等的实数根: x 1 , 2 = − − --> b ± ± --> b 2 − − --> 4 a c 2 a {\displaystyle x_{1,2}={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}}
若 Δ Δ --> = 0 {\displaystyle \Delta =0\,} ,该方程有两个相等的实数根: x 1 , 2 = − − --> b 2 a {\displaystyle x_{1,2}={\frac {-b}{2a}}}
若 Δ Δ --> < 0 {\displaystyle \Delta <0\,} ,该方程有一对共轭复数根
根与系数的关系
更多资料:韦达定理
设 x 1 {\displaystyle x_{1}\,} , x 2 {\displaystyle x_{2}\,} 是一元二次方程 a x 2 + b x + c = 0 {\displaystyle ax^{2}+bx+c=0\,} 的两根,那么
(两根之和) x 1 + x 2 = − − --> b a {\displaystyle x_{1}+x_{2}=-{\frac {b}{a}}} ,(两根之积) x 1 x 2 = c a {\displaystyle x_{1}x_{2}={\frac {c}{a}}}
一元二次方程
二元二次方程
高元二次方程
求根公式的由来
中亚细亚的花拉子米(约780-约850) 在公元820年左右出版了《代数学》。书中给出了一元二次方程的求根公式,并把方程的未知数叫做“根”,其后译成拉丁文 radix 。
我们通常把 x = − − --> b ± ± --> b 2 − − --> 4 a c 2 a {\displaystyle x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}} 称之为 a x 2 + b x + c = 0 {\displaystyle ax^{2}+bx+c=0\,} 的求根公式: a x 2 + b x + c = 0 x 2 + b a x + c a = 0 x 2 + b a x + ( b 2 a ) 2 − − --> ( b 2 a ) 2 + c a = 0 ( x + b 2 a ) 2 − − --> b 2 4 a 2 + c a = 0 ( x + b 2 a ) 2 = b 2 4 a 2 − − --> c a ( x + b 2 a ) 2 = b 2 − − --> 4 a c 4 a 2 x + b 2 a = ± ± --> b 2 − − --> 4 a c 2 a x = − − --> b ± ± --> b 2 − − --> 4 a c 2 a {\displaystyle {\begin{aligned}ax^{2}+bx+c&=0\\x^{2}+{\frac {b}{a}}x+{\frac {c}{a}}&=0\\x^{2}+{\frac {b}{a}}x+\left({\frac {b}{2a}}\right)^{2}-\left({\frac {b}{2a}}\right)^{2}+{\frac {c}{a}}&=0\\\left(x+{\frac {b}{2a}}\right)^{2}-{\frac {b^{2}}{4a^{2}}}+{\frac {c}{a}}&=0\\\left(x+{\frac {b}{2a}}\right)^{2}&={\frac {b^{2}}{4a^{2}}}-{\frac {c}{a}}\\\left(x+{\frac {b}{2a}}\right)^{2}&={\frac {b^{2}-4ac}{4a^{2}}}\\x+{\frac {b}{2a}}&={\frac {\pm {\sqrt {b^{2}-4ac}}}{2a}}\\x&={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}\end{aligned}}}
或不将 x 2 {\displaystyle x^{2}} 系数化为1:
a x 2 + b x + c = 0 a x 2 + b x + ( b 2 a ) 2 = ( b 2 a ) 2 − − --> c ( x a + b 2 a ) 2 = ( b 2 a ) 2 − − --> c x a + b 2 a = ± ± --> ( b 2 a ) 2 − − --> c x a + b 2 a = ± ± --> b 2 4 a − − --> c x + b 2 a = ± ± --> b 2 4 a 2 − − --> c a x + b 2 a = ± ± --> b 2 4 a 2 − − --> 4 a c 4 a 2 x = − − --> b 2 a ± ± --> b 2 − − --> 4 a c 4 a 2 x = − − --> b ± ± --> b 2 − − --> 4 a c 2 a {\displaystyle {\begin{aligned}ax^{2}+bx+c&=0\\ax^{2}+bx+\left({\frac {b}{2{\sqrt {a}}}}\right)^{2}&=\left({\frac {b}{2{\sqrt {a}}}}\right)^{2}-c\\\left(x{\sqrt {a}}+{\frac {b}{2{\sqrt {a}}}}\right)^{2}&=\left({\frac {b}{2{\sqrt {a}}}}\right)^{2}-c\\x{\sqrt {a}}+{\frac {b}{2{\sqrt {a}}}}&=\pm {\sqrt {\left({\frac {b}{2{\sqrt {a}}}}\right)^{2}-c}}\\x{\sqrt {a}}+{\frac {b}{2{\sqrt {a}}}}&=\pm {\sqrt {{\frac {b^{2}}{4a}}-c}}\\x+{\frac {b}{2a}}&=\pm {\sqrt {{\frac {b^{2}}{4a^{2}}}-{\frac {c}{a}}}}\\x+{\frac {b}{2a}}&=\pm {\sqrt {{\frac {b^{2}}{4a^{2}}}-{\frac {4ac}{4a^{2}}}}}\\x&=-{\frac {b}{2a}}\pm {\sqrt {\frac {b^{2}-4ac}{4a^{2}}}}\\x&={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}\end{aligned}}}
极值
极值的公式
设 y = a x 2 + b x + c {\displaystyle y=ax^{2}+bx+c\,} , 将其求导,可得出
设 d y d x = 0 {\displaystyle {\frac {{\mathop {\mbox{d}}}y}{{\mathop {\mbox{d}}}x}}=0} ,可得 x {\displaystyle x\,} 在 y {\displaystyle y\,} 中的极值(极大值或极小值) x e {\displaystyle x_{e}\,} 满足:
将 x e = − − --> b 2 a {\displaystyle x_{e}=-{\frac {b}{2a}}} 代入 y {\displaystyle y\,} ,可得 y {\displaystyle y\,} 的极值 y e {\displaystyle y_{e}\,} :
极值的类型
由函数取极值的充分条件可知: f ″ ( x e ) < 0 {\displaystyle f""(x_{e}) 0 {\displaystyle f""(x_{e})>0\,} , x e {\displaystyle x_{e}\,} 是 f ( x ) {\displaystyle f(x)\,} 的极小值点; f ″ ( x e ) = 0 {\displaystyle f""(x_{e})=0\,} , x e {\displaystyle x_{e}\,} 是 f ( x ) {\displaystyl拐点f(x)\,} 的拐点)。 由 d 2 y d x 2 = 2 a {\displaystyle {\frac {{\mathop {\mbox{d}}}^{2}y}{{\mathop {\mbox{d}}}x^{2}}}=2a} 可知: a < 0 {\displaystyle a 0 {\displaystyle a>0\,} , y {\displaystyle y\,} 的极值 y e {\displaystyle y_{e}\,} 为极小值; a = 0 {\displaystyle a=0\,} , y {\displaystyle y\,} 并非二次函数。 二次函数亦没有拐点(反曲点)。
参见
一次方程
抛物线
配方法
圆锥曲线
免责声明:以上内容版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。感谢每一位辛勤著写的作者,感谢每一位的分享。

- 有价值
- 一般般
- 没价值








关于我们

APP下载