定义项的递归定义一个变量或一个常量符号或f(t1,...,tn){\displaystylef(t_{1},...,t_{n})\,}，这里的f{\displaystylef\,}是一个n-元函数符号，而t1,...,tn{\displaystylet_{1},...,t_{n}\,}是项。公式的递归定义t1=t2{\displaystylet_{1}=t_{2}\,}，这里的t1{\displaystylet_{1}\,}和t2{\displaystylet_{2}\,}是项或R(t1,...,tn){\displaystyleR(t_{1},...,t_{n})\,}，这里的R{\displaystyleR\,}是一个n-元关系符号，而t1,...,tn{\displaystylet_{1},...,t_{n}\,}是项或(¬¬-->φφ-->){\disp...

泰勒公式泰勒公式的初衷是用多项式来近似表示函数在某点周围的情况。比如说，指数函数e在x=0的附近可以用以下多项式来近似地表示：称为指数函数在0处的n阶泰勒展开公式。这个公式只对0附近的x有用，x离0越远，这个公式就越不准确。实际函数值和多项式的偏差称为泰勒公式的余项。泰勒定理对于一般的函数，泰勒公式的系数的选择依赖于函数在一点的各阶导数值。这个想法的原由可以由微分的定义开始。微分是函数在一点附近的最佳线性近似：也就是说f(a+h)≈≈-->f(a)+f′′-->(a)h{\displaystylef(a+h)\approxf(a)+f^{\prime}(a)h}，或f(x)≈≈-->f(a)+f′′-->(a)(x−−-->a){\displaystylef(x)\approxf(a)+f^{\prime}(a)(x-a)}。注意到f(x){\displaystylef(x)}和f(a)+...

历史这个公式是亚伯拉罕·棣莫弗首先发现的，形式为：斯特灵证明了公式中c=2ππ-->{\displaystylec={\sqrt{2\pi}}}。更加精确的形式是雅克·比内发现的。推导这个公式，以及误差的估计，可以推导如下。我们不直接估计n!，而是考虑它的自然对数：即:这个方程的右面是积分∫∫-->1nln⁡⁡-->(x)dx=nln⁡⁡-->n−−-->n+1{\displaystyle\int_{1}^{n}\ln(x)\,dx=n\lnn-n+1}的近似值（利用欧拉法麦克劳林它的误差由欧拉-麦克劳林公式给出：其中Bk是伯努利数，Rm,n是欧拉-麦克劳林公式中的余项。取极限，可得：我们把这个极限记为y。由于欧拉-麦克劳林公式中的余项Rm,n满足：其中我们用到了大O符号，与以上的方程结合，便得出对数形式的近似公式：两边取指数，并选择任何正整数m，我们便得到了...

美国作家杰克·伦敦（1876―1916年）收到一位贵族小姐的求爱信：“亲爱的杰克·伦敦，用你的美名加上我的高贵地位，再乘上万能的黄金。足以使我们建立起一个天堂所不能比拟的美满家庭。”杰克·伦敦在回信中说：“你列出的那道爱情公式，我看开平方才有意义，而我们两个的心就是它们的平方根；可是很遗憾，这个平方根开出来的却是负数。”

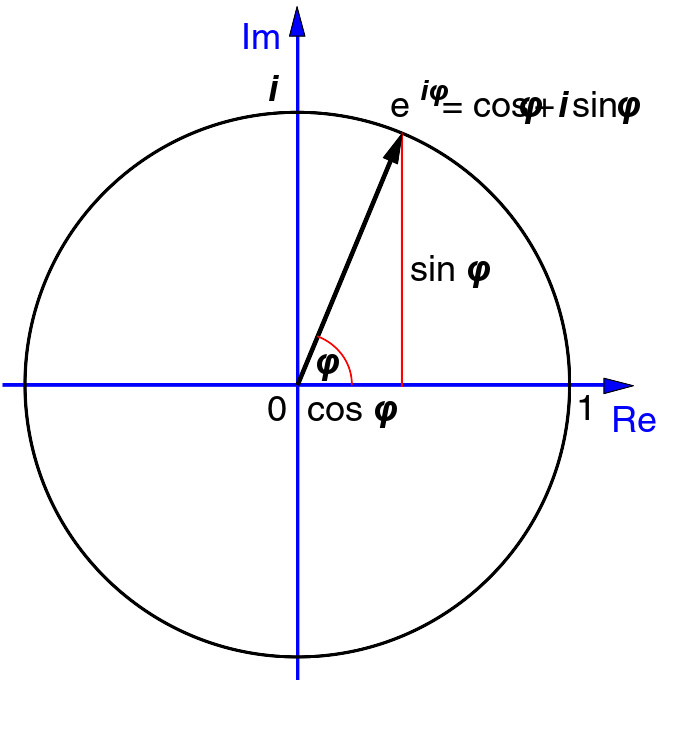
形式对于任意实数x{\displaystylex\,}，以下恒真：由此也可以推导出sin⁡⁡-->x=eix−−-->e−−-->ix2i{\displaystyle\sinx={\frac{e^{ix}-e^{-ix}}{2i}}}及cos⁡⁡-->x=eix+e−−-->ix2{\displaystyle\cosx={\frac{e^{ix}+e^{-ix}}{2}}}。当x=ππ-->{\displa欧拉tylex=\pi\,}时，欧拉公式的特殊形式为eiππ-->+1=0{\displaystyle欧拉恒等式\pi}+1=0\,}。（参见欧拉恒等式）cis函数在复分析领域，欧拉公式亦可以以函数的形式表示并且一般定义域为θθ-->∈∈-->R{\displaystyle\theta\in\mathbb{R}\,}，值域为θθ--&...