历史

  窗户上的雨滴使得金门大桥看起来变得倒立和变小了。

欧洲有关透镜的文字记载，最早出现在古希腊，在阿里斯托芬的戏剧云彩（纪元前424年）中就提到了烧玻璃（一种凸透镜，可以汇聚太阳光来点火）；以《自然史》（ Naturalis Historia ）一书留名后世的古罗马作家、科学家，老普林尼(23年–79年)的文字叙述中也表示罗马帝国知道烧玻璃， 并且提及矫正透镜第一个可能的用途：说是尼禄用于观看格斗比赛使用的绿宝石。 （虽然可供参考的资料并不明确，但推测是改正近视的凹透镜。）他与小普林尼和小瑟内卡 (Seneca the Younger，前3年–65年)都描述充满了水的玻璃球有放大的功能。阿拉伯的数学家Ibn Sahl（c.940年–c.1000年）使用现在所知的史奈尔定律计算透镜的形状； Ibn al-Haitham（965年–1038年）撰写了第一篇光学的论文，描述透镜如何在人眼睛的视网膜上成像。最古老的人工制品是在美索不达米亚的尼尼微被挖掘出来的石英透镜，大约出现在纪元前640年。

中国战国时期的《墨子》一书，叙述了透镜成像规律。《墨子·经下》及《墨子·经说下》的第二四、二五条，便分别叙述了凹透镜和凸透镜的成像规律。

最近在维京人的港口小镇Fröjel，现在瑞典的哥特兰，进行的挖掘工作，显示在11到12世纪已经能够制造水晶透镜，而且检视其品质可以与50年代的消球差透镜相比较，维京透镜可以聚集太阳光点燃火种。

眼镜大约在1280年的意大利被发明，之后透镜才被普遍的利用。尼古拉斯·库沙则被认为是第一位将凹透镜用于治疗近视的人，时间则是1451年。

恩斯特·阿贝（1860年）提出的阿贝正弦条件，描述了透镜或其他光学系统要能在离开光轴的区域上产生如同在光轴上一样清晰的影像所必须要的条件。他改革了光学仪器，例如显微镜的设计，并且帮助创立了卡尔·蔡斯公司，不仅成为光学仪器的供应商，还主导了光学仪器的研究与发展。

透镜结构

球面透镜和非球面透镜

球面透镜的“球面的曲率”是恒定的，也就是透镜前面和后面的表面都分别是球形表面的一部分。每个表面可以是凸面（从透镜向外凸起）、凹面（凹陷进入透镜）或是“平面”（平坦的）。透镜前后表面的球面中心点的连线称为透镜的 光轴 ，几乎在所有的状况下，透镜的光轴会通过透镜的物理学上的中心。

非球面透镜的曲率半径随着中心轴而变化，具有更佳的曲率半径，可以维持良好的像差修正。

凸透镜和凹透镜

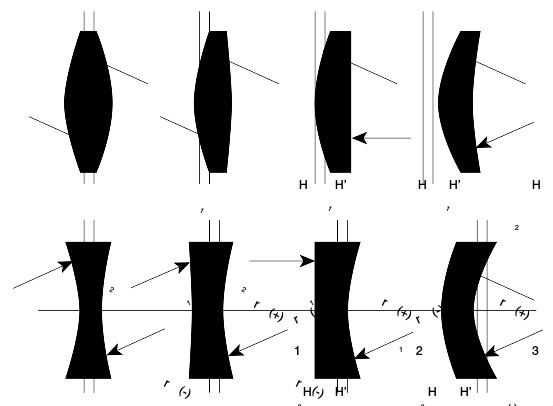
  1-4为凸透镜，5-8为凹透镜，其中：1 - 对称双凸透镜， 2 - 非对称双凸透镜， 3 - 平凸透镜4 - 凹凸透镜（凸度大于凹度）， 5 - 对称双凹透镜6 - 非对称双凹透镜， 7 - 平凹透镜， 8 - 凸凹透镜（凹度大于凸度）

透镜是依据两个光学表面的曲度来分类， 双凸透镜 （或是 凸透镜 ）的两面都是突起的，换言之，一个透镜的两面都是凹陷的称为 双凹透镜 （ 凹透镜 ）。如果有一个表面是平坦的，这个透镜称为 平凸透镜 或 平凹透镜 ，要由另一个表面的曲度来决定。透镜的一个表面凸起，另一个表面凹陷，称为 凸凹透镜 ，而如果这两个面的曲度相同，则称为 新月透镜 。（通常， 新月透镜 泛指所有形式的凸凹透镜。）

通过透镜两个面中心的直线叫透镜的主光轴，简称主轴或光轴；透镜的中心称为光心。

如果透镜是双凸透镜或平凸透镜，一束被校准或是平行的光柱，以平行于光轴的方向前进穿过镜身后将会透镜后方汇聚（或是聚焦）在轴上的一个点，这个点称为焦点，与透镜的距离称为焦距。在这种情况下，透镜称为“正透镜”、“凸透镜”或“汇聚透镜”。由于凸透镜能汇聚光线，它可用于生火。另外，许多设备中装有凸透镜，来形成物体放大的像。

如果透镜是双凹透镜或平凹透镜，一束被校准或是平行的光柱，以平行于光轴的方向前进穿过镜身后将会透镜后方扩散（或是发散）。在这种情况下，透镜称为“负透镜”、“凹透镜”或“发散透镜”。通过后发散的光线看起来像是从透镜前方光轴上的一个点发射出去的，这个点称为焦点，与透镜的距离称为焦距。与正透镜相反，其焦距是负值。由于凹透镜能发散光线，其成像较小、视野较广，常用于制作近视眼镜。

如果透镜是凸凹透镜，那么是汇聚或发散透镜就要看这两个曲面表面的相对曲率来决定了。如果两者相等（新月透镜），则通过的光柱既不汇聚也不发散。

制镜者方程

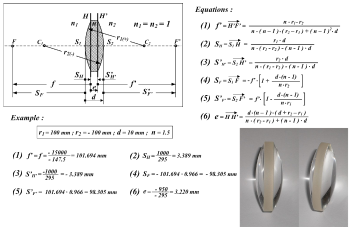
  透镜方程

对任何一个特殊的透镜，焦长可以经由 制镜者方程 计算而得：

此处

曲率半径 R 1 和 R 2 的符号(正负值)

透镜曲率半径的符号是由透镜表面是汇聚或发散来决定的，这个符号用来表示变化的方式，但是在这篇文章中， R 1 是正值，表示第一个面是凸面，而如果 R 1 是负值，这个面就是凹面。但在透镜后方的意义就相反了：如果 R 2 是正值，这个面是凹面，而如果 R 2 是负值，这个面是凸面。如果半径是无限大，这表示是一个平面。

薄透镜方程

如果厚度 d 与曲率半径 R 1 和 R 2 比较是很小的数值，这个透镜称为 薄透镜 ，而焦长 f 的估计值可以下面近似的公式计算得到：

焦长 f 是正值，透镜是汇聚透镜；是负值，透镜是发散透镜；无限大，则是新月透镜。焦长的倒数1/ f 被称为透镜的 度数 ，因此新月透镜的度数为0度，透镜的度是以 屈光度 来测量，它的单位是 (m ).

当光线由后方向前方行进时，透镜与光线由前方射入时有相同的焦长。当光线由前方进入透镜时，还有一些其他的特质，例如像差，则不一定会与光线由后方进入时相同。

成像特点

物体到透镜光心的距离称为物距，而物体经透镜所成的像到透镜光心的距离称为像距。则凸透镜与凹透镜的成像满足以下公式： 1 u + 1 v = 1 f {\displaystyle {\frac {1}{u}}+{\frac {1}{v}}={\frac {1}{f}}} ，其中 u {\displaystyle u} 为物距， v {\displaystyle v} 为像距， f {\displaystyle f} 为焦距。凸透镜的成像、虚物对凹透镜的成像具体规律如下表，其中若未特别说明，则凸透镜所成像均为实像，凹透镜所成像均为虚像：

物体所成像的移动方向总是与物体移动方向相同，而二者的相对速度则与相对大小有关。实物在镜前对凹透镜所成的像一律满足 v < f {\displaystyle v ，成缩小正立的虚像，近视眼镜便是用到此原理。

透镜中心（optical center）

  经由近视眼镜（凹透镜）看见的西雅图市影像。

理论上，当光线穿过光心（optical center），应该会出现偏差（deviation）。 除了球面透镜，凸透镜、凹透镜、平凸透镜、平凹透镜、凸凹透镜的弧面都是由抛物面组成的，加上由于透镜通常是很薄的，在一定角度，光线穿过中心不会出现看得见的偏差（visible deviation）。

在制造透镜的时候，弧面是经过设计的，在一定角度，光线穿过中心时，投射线与折射线会尽量变成平行。而由于透镜通常是很薄的，令近乎平行的投射线与折射线像一条直线一样。

实际应用

凹透镜：近视眼镜

凸透镜：放大镜、幻灯机、鱼眼镜头、远视眼镜

另外，相机镜头、显微镜、光学望远镜等也会用到多组透镜。

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。