分岔类型

分岔可以分为以下的二种类型：

局部分岔（Local bifurcations）是指分岔特性可以用局部稳定性完全分析的分岔，一般会用参数通过临界值时，平衡点、周期性轨迹或其他固定点的局部稳定性。

全域分岔（Global bifurcations）是指分岔特性无法用局部稳定性完全分析的分岔，一般是指较大的不变集彼此重叠，或是和系统的平衡点重叠，这无法只靠平衡点的稳定性分析来求得。

局部分岔

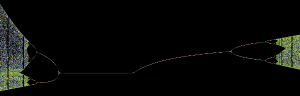
  逐渐变成有序的周期对半分岔（L），之后是逐渐变成混沌的周期加倍分岔（R）

局部分岔是指因参数变化，因此改变平衡点（或是不动点）稳定性的情形，对应平衡点特征值的实部由正变负或是由负变正，在离散系统中（会由映射描述），是指不动点其弗洛凯乘子的模为1。这二种情形下，平衡点在分岔时都是非双曲线的。

局部分岔有一个特性，只要控制分岔参数，可以将系统相图中的拓朴变化限制在分岔点附近任意小的区域中，因此称为局部分岔。

考虑用以下常微分方程描述的连续动态系统

若在 ( x 0 , λ λ --> 0 ) {\displaystyle (x_{0},\lambda _{0})} 位置的雅可比矩阵 d f x 0 , λ λ --> 0 {\displaystyle {\textrm {d}}f_{x_{0},\lambda _{0}}} 有实部为0的特征值，表示在此点有局部分岔。若特征值为0，表示此分岔为稳态的分岔，但若特征值为虚数霍普夫是 霍普夫分岔 （ 英语 ： Hopf bifurcation ） 。

若是离散系统

若在 ( x 0 , λ λ --> 0 ) {\displaystyle (x_{0},\lambda _{0})} 的矩阵 d f x 0 , λ λ --> 0 {\displaystyle {\textrm {d}}f_{x_{0},\lambda _{0}}} 有模数为1的特征值，表示有局部分岔。若特征值等于1，分岔可能是 鞍结分岔 （ 英语 ： saddle-node bifurcation ） 、 跨临界分岔 （ 英语 ： transcritical bifurcation ） 或 叉式分岔 （ 英语 ： pitchfork bifurcation ） ，若特征值等于-1，表示是 周期加倍分岔 （ 英语 ： period-doubling bifurcation ） ，否则则为 霍普夫分岔 （ 英语 ： Hopf bifurcation ） 。

局部分岔的例子有：

鞍结分岔 （ 英语 ： saddle-node bifurcation ） （fold分岔）

跨临界分岔 （ 英语 ： transcritical bifurcation ）

叉式分岔 （ 英语 ： pitchfork bifurcation ）

周期加倍分岔 （ 英语 ： period-doubling bifurcation ） （flip分岔）

霍普夫分岔 （ 英语 ： Hopf bifurcation ）

Neimark–Sacker分岔（二次霍普夫分岔）

全域分岔

全域分岔是指较大的不变集（如周期性轨迹）和平衡点重叠。全域分岔也会改变相图上的拓朴，而且其变化不会像局部分岔一様限制在一个小区域，因此称为全域分岔。

全域分岔的例子有：

同宿分岔 （ 英语 ： Homoclinic bifurcation ） 是指极限环和一个鞍点重叠。

异宿分岔 （ 英语 ： Heteroclinic bifurcation ） 是指极限环和二个或多个鞍点重叠。

无限周期分岔 （ 英语 ： Infinite-period bifurcation ） 是指在极限环上有稳定节点和鞍点同时出现。

蓝天突变 （ 英语 ： Blue sky catastrophe ） 是指极限环和一个nonhyperbolic cycle重叠。

全域分岔有时会和像奇异吸引子之间更复杂的结构有关，如一种称为 危机 （ 英语 ： Crisis (dynamical systems) ） 的现象就是指当动态系统的参数变化时，奇异吸引子突然出现或是突然消失。

分岔的余维数

分岔的余维数是指动态系统中需变动几个参数，才会使分岔现象出现。鞍结分岔及霍普夫分岔是常见的局部分岔中，实际余维数为1的二个分岔（其他分岔的余维数都大于1）。不过跨临界分岔及叉式分岔的正规式可以写成只有一个参数的形式，因此也可以视为余维数为1的分岔。

Bogdanov-Takens 分岔 （ 英语 ： Bogdanov–Takens bifurcation ） 是一个有较多研究，余维数为2分岔的一个例子。

在半经典力学及量子力学上的应用

分岔理论已用在连结量子系统及经典力学系统的动态中，可以用在原子系统 、分子系统 及谐振隧穿二极管 。分岔理论已用到激光动力学 的研究中，也用在许多在实验上难以处理的理论例子中，例如kicked top 及耦合量子阱 。将量子系统及古典力动方程中分岔相连结的主要原因是在分岔时，古典力学轨道的signature会变大，正如 Martin Gutzwiller （ 英语 ： Martin Gutzwiller ） 在有关 量子混沌 （ 英语 ： quantum chaos ） 中的研究所提出的一样 。许多分岔都研究来连结古典力学和量子力学，像是鞍结分岔、霍普夫分岔、umbilic分岔、周期加倍分岔、重新连接分叉（reconnection bifurcation）、切线分叉（tangent bifurcation）及尖分叉（cusp bifurcation）。

相关条目

数学主题首页

突变理论 （ 英语 ： Catastrophe theory ）

相图 (动态系统)

费根鲍姆常数

分叉内存 （ 英语 ： Bifurcation memory ）

分枝图 （ 英语 ： Bifurcation diagram ）

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。