概述

保守力可以视为一种使机械能守恒的作用力。在一个孤立系统里，假若所有的作用力都是保守力，则此系统的机械能守恒。在这里，机械能指的是动能与势能的总合。

思考一个闭合路径，假设，感受着某作用力，一个粒子从初始位置A移动经过任意闭合路径后，又回到位置 A ，而此作用力所做于粒子的机械功都等于零，则此作用力满足保守力的条件，可以被分类为保守力。请注意，对于这物理系统，很可能有其他的作用力施加于粒子，但是，这分类只专注于指定的作用力，忽略其他的作用力。当然，根据叠加原理，这分类也可以专注于几个作用力的合力。例如引力、弹簧力、磁场力（依照某些定义而定，稍后会加以详细说明）、电场力（伴随的磁场与时间无关，请参阅法拉第电磁感应定律）等等，都是保守力；而摩擦力和空气阻力是典型的非保守力。

对于非保守力，由于能量守恒，损耗的能量必需被传输到其他地方。通常，能量会转换为热能，例如，摩擦力会产生热能，有时候，还会产生声能。对于移动中的船只，水的阻力会将船只的机械能转换为热能、声能、以及在尾流边缘的波能。由于热力学第二定律，这些能量损耗是不可逆的。

路径独立性

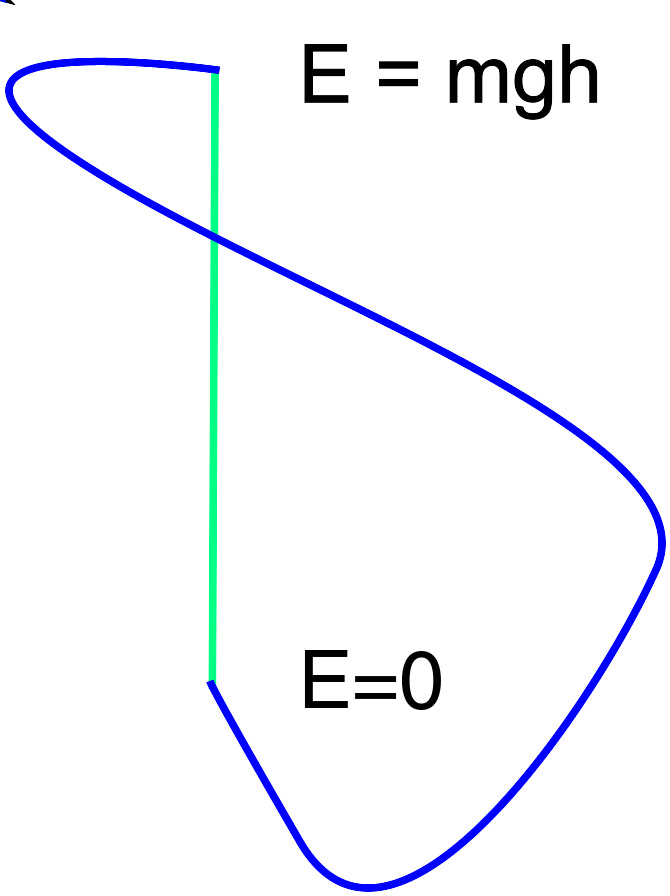
因为引力是保守力，它对于一个物体所做的机械功，只跟物体位置高度的差值有关。

闭合路径思想实验得到的直接结果是，保守力对于一个粒子所做的机械功，跟移动路径无关；还有，这机械功等于，终结势能减去初始势能。试着证明这句话的正确性。设想从点 A 到点 B 有两条不同的路径。选择路径 1 从点 A 移动到点 B ，然后选择路径 2 反方向从点 B 移动到点 A ，粒子能量的改变是零 。因此，不管是选择路径 1 或路径 2 ，从点 A 移动到点 B ，所做的机械功相等。保守力所做的机械功与经过哪一条路径无关，只要两条路径的初始点与终结点相同 。

举例而言，假设一个小孩从一个滑梯上滑下来，从滑梯的顶端到底端，不论滑梯的形状，直线型或螺旋型，引力对于这小孩所做的机械功都一样的。引力所做的机械功，只跟这小孩的落差有关。

保守力的性质

设定 F{\displaystyle \mathbf {F} } 为在空间任意位置良好定义（或空间内单连通的区域）的矢量场，假若它满足以下三个等价的条件中任意一个条件，则可称此矢量场为保守矢量场：

保守力因为可以保守机械能而得名。最常见的保守力为引力、电场力（伴随的磁场与时间无关，请参阅法拉第电磁感应定律）、弹簧力。

数学证明

1⇒2：

2⇒3：

3⇒1：

总结，这三个条件彼此等价。由于符合第二个条件就等于通过保守力的闭合路径考试。所以，只要满足上述三个条件的任何一条件，施加于粒子的作用力就是保守力。

磁场力

很多种作用力不是力矢量场，特别是跟速度有关的作用力。对于这些案例，上述三个条件并不数学等价。例如，磁场力满足第二个条件（由于作用于带电粒子的磁场力所做的机械功永远为零），但是不满足第三个条件，而第一个条件更是不存在定义──磁场力不是矢量场，磁场力与速度有关，必需先给定速度函数的形式，才能计算磁场力的旋度。

所以，有一些物理学者将磁场力分类为保守力，而又有一些物理学者反对这样分类。磁场力是一个特别案例；大多数跟速度有关的作用力，像摩擦力，不能满足上述三个条件中的任意一个条件，因此，可以明确地分类为非保守力。

非保守力

在经典力学里，当计算一个物理系统的运动时，为了简易分析与计算，自由度被忽略，因此会出现非保守力。举例而言，摩擦力可以不被视为一种非保守力，而是每一个分子在运动时互相作用的力。可是，这样做，就不能应用统计力学，而必须特别计算每一个分子的运动。对于宏观系统，非保守力的概算，比起额外几百万自由度的计算，会简单很多。非保守力的案例有摩擦力、非弹性物质的应力。

在广义相对论里，引力是非保守力，这可以从水星近日点的反常进动观察得着。但是，应力-能量张量是守恒的。

参阅

保守矢量场

螺线矢量场

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。