起源

牛顿法最初由艾萨克·牛顿在《流数法》（Method of Fluxions，1671年完成，在牛顿死后的1736年公开发表）中提出。约瑟夫·拉弗森也曾于1690年在Analysis Aequationum中提出此方法。

方法说明

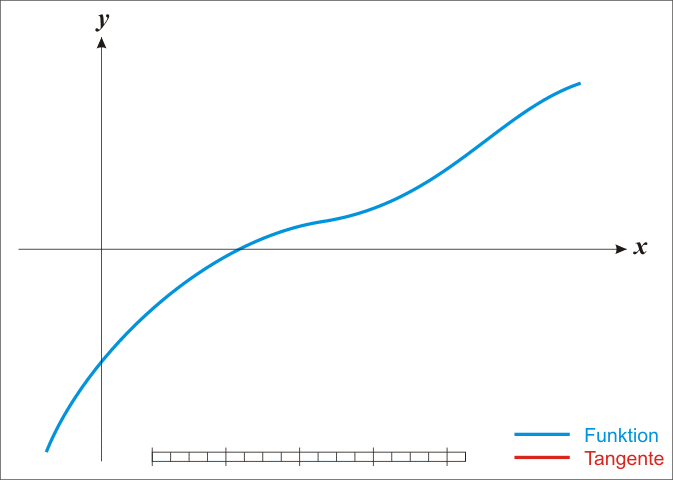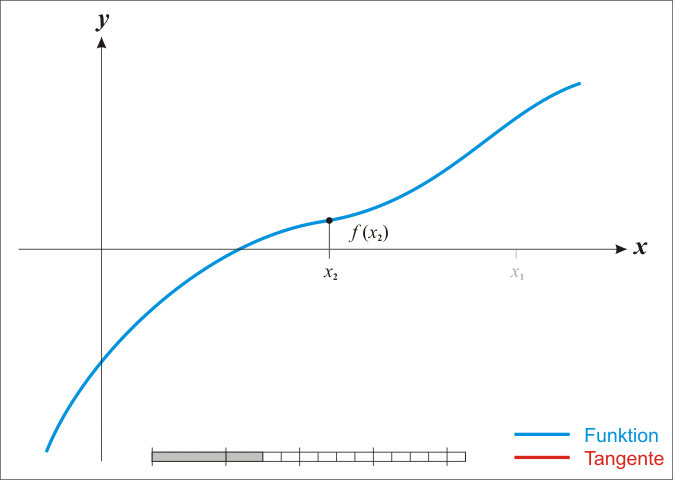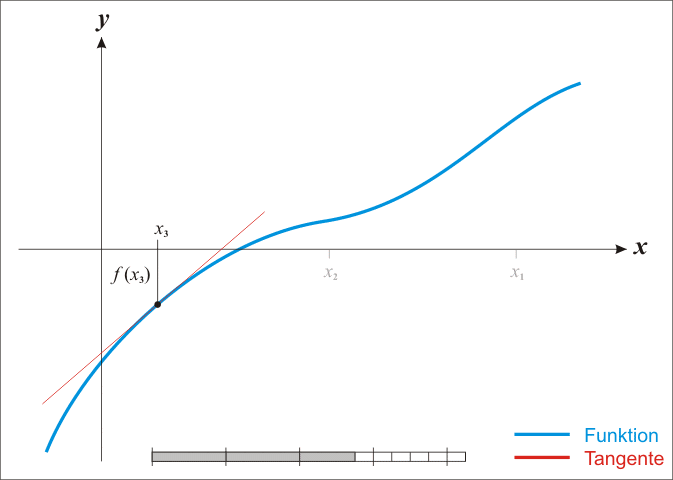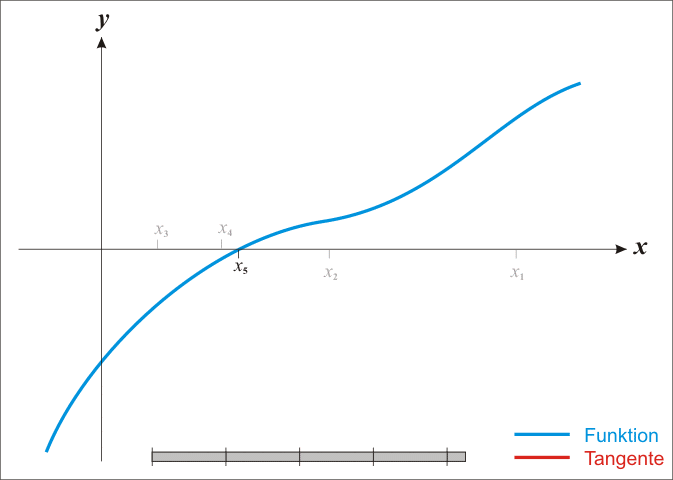
蓝线表示方程f{\displaystyle f}

而红线表示切线。可以看出xn+1{\displaystyle x_{n+1}}

比xn{\displaystyle x_{n}}

更靠近f{\displaystyle f}

所要求的根x{\displaystyle x}

。

首先，选择一个接近函数f(x){\displaystyle f(x)}零点的x0{\displaystyle x_{0}}，计算相应的f(x0){\displaystyle f(x_{0})}和切线斜率f′(x0){\displaystyle f"(x_{0})}（这里f′{\displaystyle f"}表示函数f{\displaystyle f}的导数）。然后我们计算穿过点(x0,f(x0)){\displaystyle (x_{0},f(x_{0}))}并且斜率为f′(x0){\displaystyle f"(x_{0})}的直线和x{\displaystyle x}轴的交点的x{\displaystyle x}坐标，也就是求如下方程的解：

我们将新求得的点的x{\displaystyle x}坐标命名为x1{\displaystyle x_{1}}，通常x1{\displaystyle x_{1}}会比x0{\displaystyle x_{0}}更接近方程f(x)=0{\displaystyle f(x)=0}的解。因此我们现在可以利用x1{\displaystyle x_{1}}开始下一轮迭代。迭代公式可化简为如下所示：

已经证明，如果f′{\displaystyle f"}是连续的，并且待求的零点x{\displaystyle x}是孤立的，那么在零点x{\displaystyle x}周围存在一个区域，只要初始值x0{\displaystyle x_{0}}位于这个邻近区域内，那么牛顿法必定收敛。

并且，如果f′(x)≠ ≠ -->0{\displaystyle f"(x)\neq 0}，那么牛顿法将具有平方收敛的性能。粗略的说，这意味着每迭代一次，牛顿法结果的有效数字将增加一倍。

其它例子

第一个例子

求方程cos⁡ ⁡ -->(x)− − -->x3=0{\displaystyle \cos(x)-x^{3}=0}的根。令f(x)=cos⁡ ⁡ -->(x)− − -->x3{\displaystyle f(x)=\cos(x)-x^{3}}，两边求导，得f′(x)=− − -->sin⁡ ⁡ -->(x)− − -->3x2{\displaystyle f"(x)=-\sin(x)-3x^{2}}。由于− − -->1≤ ≤ -->cos⁡ ⁡ -->(x)≤ ≤ -->1(∀ ∀ -->x){\displaystyle -1\leq \cos(x)\leq 1(\forall x)}，则− − -->1≤ ≤ -->x3≤ ≤ -->1{\displaystyle -1\leq x^{3}\leq 1}，即− − -->1≤ ≤ -->x≤ ≤ -->1{\displaystyle -1\leq x\leq 1}，可知方程的根位于0{\displaystyle 0}和1{\displaystyle 1}之间。我们从x0=0.5{\displaystyle x_{0}=0.5}开始。

第二个例子

牛顿法亦可发挥与泰勒展开式，对于函式展开的功能。

求a{\displaystyle a}的m{\displaystyle m}次方根。

xm− − -->a=0{\displaystyle x^{m}-a=0}

设f(x)=xm− − -->a{\displaystyle f(x)=x^{m}-a}，f′(x)=mxm− − -->1{\displaystyle f"(x)=mx^{m-1}}

而a的m次方根，亦是x的解，

以牛顿法来迭代：

xn+1=xn− − -->f(xn)f′(xn){\displaystyle x_{n+1}=x_{n}-{\frac {f(x_{n})}{f"(x_{n})}}}

xn+1=xn− − -->xnm− − -->amxnm− − -->1{\displaystyle x_{n+1}=x_{n}-{\frac {x_{n}^{m}-a}{mx_{n}^{m-1}}}}

xn+1=xn− − -->xnm(1− − -->axn− − -->m){\displaystyle x_{n+1}=x_{n}-{\frac {x_{n}}{m}}(1-ax_{n}^{-m})}

（或 xn+1=xn− − -->1m(xn− − -->axnxnm){\displaystyle x_{n+1}=x_{n}-{\frac {1}{m}}\left(x_{n}-a{\frac {x_{n}}{x_{n}^{m}}}\right)}）

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。