定义

对于 N 点序列 { x [ n ] } 0 ≤ ≤ --> n < N {\displaystyle \left\{x[n]\right\}_{0\leq n 傅里叶的离散傅里叶变换（DFT）为

其中 e {\displaystyle e} 是自然对数的底数， i {\displaystyle i} 是虚数单位。通常以符号 F {\displaystyle {\mathcal {F}}} 表示这一变换，即

离散傅里叶变换的逆变换（IDFT）为：

可以记为：

实际上，DFT和IDFT变换式中和式前面的归一化系数并不重要。在上面的定义中，DFT和IDFT前的系数分别为 1 和 1/N 。有时会将这两个系数都改成 1 / N {\displaystyle 1/{\sqrt {N}}} 。

从连续到离散

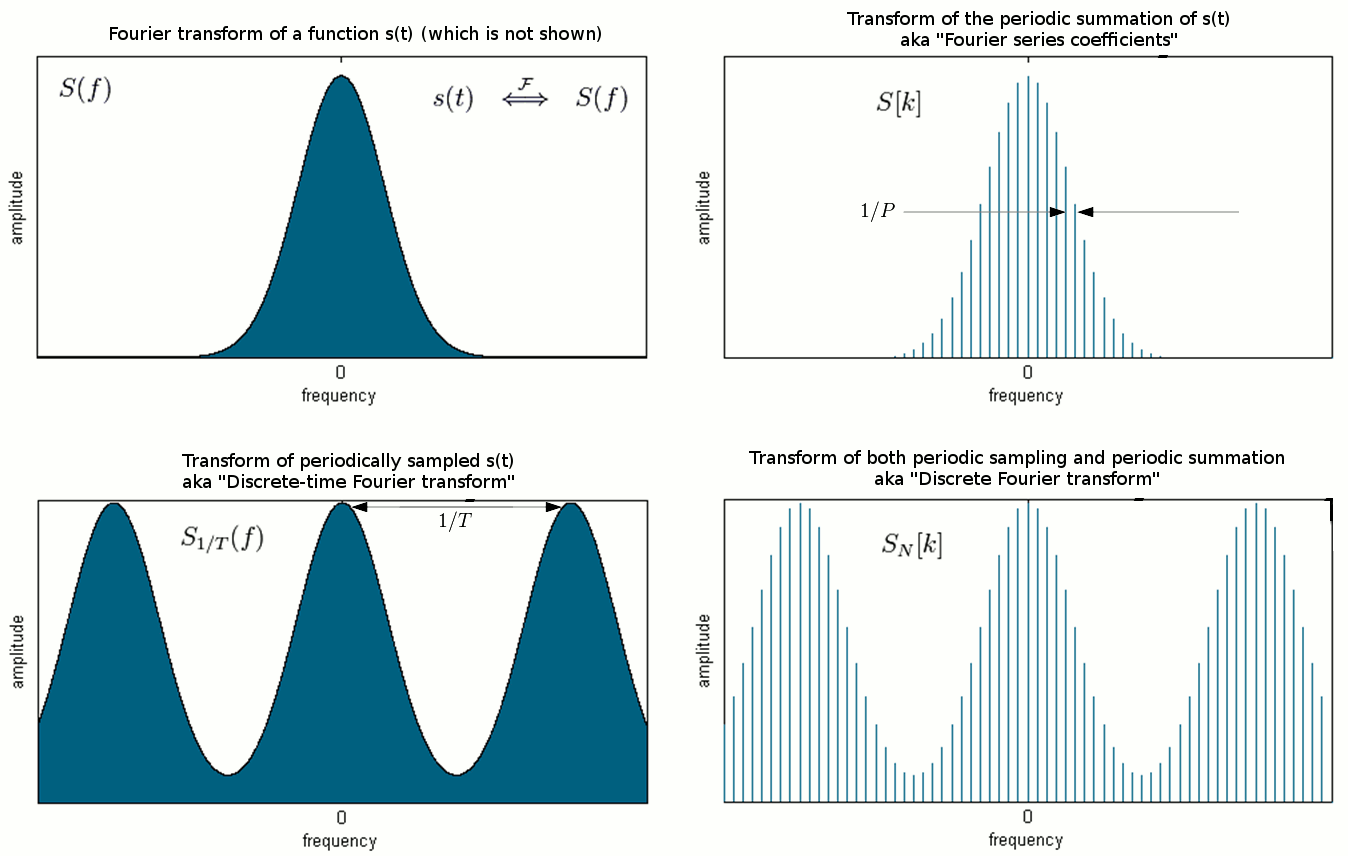
连续时间信号 x(t) 以及对应的连续傅里叶变换 x ^ ^ --> ( ω ω --> ) {\displaystyle {\hat {x}}(\omega 连续函数都是连续函数。由于数字系统只能处理有限长的离散信号，因此必须将 x {\displaystyle x} 和 x ^ ^ --> {\displaystyle {\hat {x}}} 都离散化，并且建立对应的傅里叶变换。

假设x（t）时限于[0, L]，再通过时域采样将 x ( t ) {\displaystyle x(t)} 离散化，就可以得到有限长离散信号，记为 x d i s c r e t e ( t ) {\displaystyle x_{discrete}(t)} 。设采样周期为 T ，则时域采样点数 N=L/T 。

它的傅里叶变换为

这就是 x(t) 在时域采样后的连续傅里叶变换，也就是离散时间傅里叶变换，它在频域依然是连续的。

下面将频域信号转化为有限长离散信号。与对时域信号的处理类似，假设频域信号是带限的，再经过离散化，即可得到有限长离散信号。依据采样定理，时域采样若要能完全重建原信号，频域信号 x ^ ^ --> ( ω ω --> ) {\displaystyle {\hat {x}}(\omega )} 应当带限于（0,1/（2*T））。由于时域信号时限于[0, L]，由采样定理以及时频对偶的关系，频域的采样间隔应为1/L。故，频域采样点数为：

即频域采样的点数和时域采样同为 N ，频域采样点为 { ω ω --> k = 2 π π --> k / N T } 0 ≤ ≤ --> k < N {\displaystyle \{\omega _{k}={2\pi }k/NT\}_{0\leq k 在DTFT频域上采样：

令 T=1 ，将其归一化，就得到前面定义的离散傅里叶变换。因此，DFT就是先将信号在时域离散化，求其连续傅里叶变换后，再在频域离散化的结果。

DFT与CT

下面考察离散傅里叶变换与连续傅里叶变换（CT，Continuous Fourier Transform）的关系。连续傅里叶变换

的采样为：

将这个积分以黎曼和的形式近似，有：

这一结论指出离散傅里叶变换确实是连续傅里叶变换在某种意义上的近似。不过必须注意以下两点：

时域采样必须满足采样定理

离散傅里叶变换的处理对象是时限的

为此，通常对连续信号的时域采样再做一次加窗处理（Windowing），这样就得到带限的有限长离散信号。

DFT与DTFT

离散时间傅里叶变换（DTFT）是在时域上对连续傅里叶变换的采样。DFT则是在频域上对DTFT的均匀采样。离散信号 x [ n ] {\displaystyle x[n]} （n=0,...,N-1）的DTFT为：

对 x ^ ^ --> ( e i ω ω --> ) {\displaystyle {\hat {x}}(e^{i\omega })} 在离散的频点 { ω ω --> k = k 2 π π --> N } 0 ≤ ≤ --> k < N {\displaystyle \{\omega _{k}=k{\frac {2\pi }{N}}\}_{0\leq k 上采样

即为 x 的DFT。由于DTFT在频域是周期的，所以在DTFT频域上的均匀采样也应是周期的。 x ^ ^ --> [ k ] {\displaystyle {\hat {x}}[k]} 实际上是这个周期序列的主值序列。

栅栏效应

N 点序列的DFT只能在有限的N个频点上观察频谱，这相当于从栅栏的缝隙中观察景色，对于了解信号在整个频域上的特性是不够的。为了观察到其他频率的信息，需要对原信号x[n]做一些处理，以便在不同的频点上采样。

将原来在DTFT频域上的采样点数增加到 M 点，这样采样点位置变为 { ω ω --> k ′ = e i k 2 π π --> M } 0 ≤ ≤ --> k < M {\displaystyle \{\omega "_{k}=e^{ik{\frac {2\pi }{M}}}\}_{0\leq k 。则对应的DFT成为

若在序列 x[n] 之后补上M-N个零，设为 x"[n] ，则上式变为

因此将x[n]补零再做DFT就可以得到x[n]的DTFT在其他频率上的值，相当于移动了栅栏，因而能够从其他位置进行观察。

频谱分辨率

N 点DFT的频谱分辨率是 2 π π --> / N {\displaystyle 2\pi /N} 。栅栏效应一节指出可以通过补零观察到更多的频点，但是这并不意味着补零能够提高真正的频谱分辨率。这是因为 x[n] 实际上是 x(t) 采样的主值序列，而将x[n]补零得到的 x"[n] 周期延拓之后与原来的序列并不相同，也不是 x(t) 的采样。因此 x ^ ^ --> ′ {\displaystyle {\hat {x}}"} 与 x ^ ^ --> {\displaystyle {\hat {x}}} 是不同离散信号的频谱。对于补零至M点的x"的DFT，只能说它的分辨率 2 π π --> / M {\displaystyle 2\pi /M} 仅具有计算上的意义， x ^ ^ --> ′ {\displaystyle {\hat {x}}"} 并不是真正的、物理意义上的频谱。频谱分辨率的提高只能在满足采样定理的条件下增加时域采样长度来实现。

从空间的角度分析

周期为N的离散信号构成一个 N 维欧几里得空间 C N {\displaystyle \mathbb {C} ^{N}} 。在这一空间上两个信号 x 和 y 的内积定义为

下面给出 C N {\displaystyle \mathbb {C} ^{N}} 上的一组正交基：

将信号 x 在这组正交基上分解，得

令

此即为离散傅里叶变换。又

则有

此即为离散傅里叶变换的逆变换。

由此可知，在正交分解的角度上说，离散周期信号 x {\displaystyle x} 的离散傅里叶变换 x ^ ^ --> {\displaystyle {\hat {x}}} 实质上是 x {\displaystyle x} 在正交基 { e k } {\displaystyle \{e_{k}\}} 上的分量。而从线性变换的角度上说， { e k } {\displaystyle \{e_{k}\}} 是圆周卷积的特征向量， x ^ ^ --> {\displaystyle {\hat {x}}} 则是对应的特征值。

DFT与圆周卷积

根据卷积定理，离散信号x与y的圆周卷积对偶于频域上x与y离散傅里叶变换的乘积。下面揭示DFT与圆周卷积的内在关系。

对长为N的离散信号 x ~ ~ --> {\displaystyle {\tilde {x}}} 与 y ~ ~ --> {\displaystyle {\tilde {y}}} ，如果要计算它们的卷积，就必须定义 x ~ ~ --> [ n ] {\displaystyle {\tilde {x}}[n]} 与 y ~ ~ --> [ n ] {\displaystyle {\tilde {y}}[n]} 在 0≤n 之外的值。如果将 x ~ ~ --> {\displaystyle {\tilde {x}}} 与 y ~ ~ --> {\displaystyle {\tilde {y}}} 作周期为N的延拓，则有

如此，周期为N的圆周卷积：

卷积的结果仍然是以N为周期的离散信号。

前面指出， e k {\displaystyle e_{k}} 是DFT的特征向量，实际上它也是圆周卷积的特征向量。定义x与y的圆周卷积算子：

则 e k {\displaystyle e_{k}} 与y的圆周卷积为

显然，y的DFT

就是圆周卷积的特征值。

性质

完全性

离散傅里叶变换是可逆的线性变换

其中 C 表示复数集。即，任意 N -维复向量都存在DFT和IDFT，而且其DFT和IDFT也是 N -维复向量。

正交性

向量组exp（2π i kn/N ）是 N -维复数空间上的一组正交基：

其中δ kn 是Kronecker delta。

移位定理

时域信号序列 x n {\displaystyle x_{n}} 的相位移动 exp ⁡ ⁡ --> ( 2 π π --> i n m / N ) {\displaystyle \exp(2\pi inm/N)} （其中 m {\displaystyle m} 为整数）在频域反映为“循环移位”，即：频域信号序列 X k {\displaystyle X_{k}} 变为 X ( ( k − − --> m ) ) N {\displaystyle X_{((k-m))_{N}}} ，其中下标是指将 k-m 对 N 取余。类似的，由对偶性，时域信号序列的循环移位对应于频域信号序列的相移：

周期性

上文中DFT与DTFT一节已经证明，离散序列的傅里叶变换是周期的。有限长序列 x n {\displaystyle x_{n}} 的离散傅里叶变换 X k {\displaystyle X_{k}} 可以被看作是它的周期延拓序列 x ~ ~ --> n = x n m o d N {\displaystyle {\tilde {x}}_{n}=x_{n\ mod\ N}} 的离散时间傅里叶变换 X ~ ~ --> k {\displaystyle {\tilde {X}}_{k}} 。由时频对偶性可知 X k {\displaystyle X_{k}} 也可以被看作它的周期延拓的主值。

上一节的移位定理隐含着DFT的周期性，因为DFT的幅度 | X k | {\displaystyle |X_{k}|} 不受输入信号的循环移位的影响，因为时移在频域对偶于相移，循环移位仅仅使DFT的相位产生平移。周期性的边界条件在DFT的许多应用中有重要作用。解差分方程时，就假设边界条件是满足周期性的，这是一个很有用的性质（参见应用）。

普朗歇尔定理与帕塞瓦尔定理

如果 X k 和 Y k 分别是 x n 和 y n 的离散傅立叶变换，那么就有普朗歇尔定理：

其中星号表示复共扼。帕塞瓦尔定理是普朗歇尔定理的一个特例：

应用

DFT在诸多多领域中有着重要应用，下面仅是颉取的几个例子。需要指出的是，所有DFT的实际应用都依赖于计算离散傅里叶变换及其逆变换的快速算法，即快速傅里叶变换。

快速傅里叶变换

快速傅里叶变换（即FFT）是计算离散傅里叶变换及其逆变换的快速算法。按照DFT的定义计算一个长为n的序列的DFT需要的计算复杂度达到了 O ( n 2 ) {\displaystyle {\mathcal {O}}(n^{2})} ，而同样长度FFT的计算复杂度仅为 O ( n log ⁡ ⁡ --> n ) {\displaystyle {\mathcal {O}}(n\log n)} 。由于DFT的逆变换可以由DFT表示，所以DFT逆变换的计算同样可以由FFT完成。FFT算法的提出，使DFT得到了广泛的实际应用。

频谱分析

前面指出，DFT是连续傅里叶变换的近似。因此可以对连续信号x（t）均匀采样并截断以得到有限长的离散序列 { x n } {\displaystyle \{x_{n}\}\,} ，对这一序列作离散傅里叶变换，可以分析连续信号x（t）频谱的性质。前面还提到DFT应用于频谱分析需要注意的两个问题：即采样可能导致信号混叠和截断信号引起的频谱泄漏。可以通过选择适当的采样频率（见奈奎斯特频率）消减混叠。选择适当的序列长度并加窗可以抑制频谱泄漏。

数据压缩

由于人类感官的分辨能力存在极限，因此很多有损压缩算法利用这一点将语音、音频、图像、视频等信号的高频部分除去。高频信号对应于信号的细节，滤除高频信号可以在人类感官可以接受的范围内获得很高的压缩比。这一去除高频分量的处理就是通过离散傅里叶变换完成的。将时域或空域的信号转换到频域，仅储存或传输较低频率上的系数，在解压缩端采用逆变换即可重建信号。

解偏微分方程

离散傅里叶变换及其多维形式在偏微分方程的求解中也有应用。此时DFT被看作傅里叶级数的近似。傅里叶级数将函数在复指数 e 上展开，这正是微分算子的特征方程： d / dx e = in e 。因此，通过傅里叶级数的形式，线性常微分方程被转换为代数方程，而后者是很容易求解的。此时得到的结果是偏微分方程解的级数表示，只要通过DFT逆变换即可得到其一般表示。这种方法被称作谱方法或级数解法。

长整数与多项式乘法

目前长整数或多项式乘法最快速的算法是基于离散傅里叶变换的。由于整数（或多项式）乘法是逐位（或逐项）乘累加的形式，因此整数（或多项式）乘积的数字（或系数）可以用乘数数字（或乘式系数）的卷积表示。利用卷积定理，只要将数字（或系数）序列通过离散傅里叶变换变到频域，就可以将逐个乘累加的卷积变为对位的乘法，从而减少计算量，再以一次逆变换便可以得到乘法结果。需要注意整数乘法还有进位的问题。下面以多项式乘法为例说明这一应用：

假设需要计算多项式乘法 c ( x ) = a ( x )· b （ x ），这一乘积结果的各项系数的表达式实际上是线性卷积的形式。由于离散傅里叶变换对应于圆周卷积，因此需要将这两个乘式的系数按照次数升序排列，序列后“补零”，使它们的长度 d 大于两式最高项次数的和： d > deg( a ( x )) + deg( b ( x ))。然后作圆周卷积：

其中 c 就是 c ( x )系数的向量。由于圆周卷积的DFT是乘积，有：

则

利用快速傅里叶变换，这一算法的运算复杂度为 O ( N log ⁡ ⁡ --> N ) {\displaystyle {\mathcal {O}}(N\log N)} 。

OFDM

OFDM（正交频分复用）在宽带无线通信中有重要的应用。这种技术将带宽分为 N 个等间隔的子载波，可以证明这些子载波相互正交。尤其重要的是，OFDM调制可以由IDFT实现，而解调可以由DFT实现。OFDM还利用DFT的移位性质，在每个帧头部加上循环前缀（Cyclic Prefix），使得只要信道延时小于循环前缀的长度，就能消除信道延时对传输的影响。

特殊例子

数论转换

数论转换是离散傅里叶转换(DFT)的一个特例 F = Z / p {\displaystyle F=Z/p} ，此运算是根据模运算而取得的， p {\displaystyle p} 需要是素数，如此可以建构出有限域，并且存在 n {\displaystyle n} 个可以整除 ( p − − --> 1 ) {\displaystyle (p-1)}实数的实数根。如此可以得到 p = k ⋅ ⋅ --> n + 1 {\displaystyle p=k\cdot n+1} ， k {\displaystyle k} 为正整数。令 ω ω --> {\displaystyle \omega } 为第 ( p − − --> 1 ) {\displaystyle (p-1)} 个单位根，则第 n {\displaystyle n} 个单位根 α α --> {\displaystyle \alpha } 可以表示成 α α --> = ω ω --> k {\displaystyle \alpha =\omega ^{k}} 。另外，再令 N {\displaystyle N} 为 α α --> {\displaystyle \alpha } 次方 p {\displaystyle p} 模运算之循环个数。

则数论矩阵为

[ F − − --> ] = [ α α --> c r − − --> ] [ f − − --> ] {\displaystyle {\begin{bmatrix}{\underset {-}{F}}\end{bmatrix}}={\begin{bmatrix}{\underset {-}{\alpha ^{cr}}}\end{bmatrix}}{\begin{bmatrix}{\underset {-}{f}}\end{bmatrix}}}

c {\displaystyle c} 与 r {\displaystyle r} 各为 Column 与 Row 的指数(index), 令 C {\displaystyle C} 与 R {\displaystyle R} 各代表Column 与 Row 的总数，则 C = R = N {\displaystyle C=R=N} ， c ∝ ∝ --> { 0 , 1 , . . . , C − − --> 1 } , r ∝ ∝ --> { 0 , 1 , . . . , R − − --> 1 } {\displaystyle c\propto {\begin{Bmatrix}0,1,...,C-1\end{Bmatrix}},r\propto {\begin{Bmatrix}0,1,...,R-1\end{Bmatrix}}} .

举个例子来说，当 p = 5 , α α --> = 2 {\displaystyle p=5,\alpha =2} 则

α α --> 1 = 2 ( m o d 5 ) {\displaystyle \alpha ^{1}=2\qquad (mod\quad 5)}

α α --> 2 = 4 ( m o d 5 ) {\displaystyle \alpha ^{2}=4\qquad (mod\quad 5)}

α α --> 3 = 3 ( m o d 5 ) {\displaystyle \alpha ^{3}=3\qquad (mod\quad 5)}

α α --> 4 = 1 ( m o d 5 ) {\displaystyle \alpha ^{4}=1\qquad (mod\quad 5)}

因为 α α --> 4 {\displaystyle \alpha ^{4}} 经 5 {\displaystyle 5} 的模运算为 1 {\displaystyle 1} ，因此可以判定此情况为 4 {\displaystyle 4} 个次方一循环，所以 N = 4 {\displaystyle N=4} ， N {\displaystyle N} 可以整除 ( p − − --> 1 ) {\displaystyle (p-1)} 。则数论矩阵可以表示成

[ F ( 0 ) F ( 1 ) F ( 2 ) F ( 3 ) ] = [ 1 1 1 1 1 2 4 3 1 4 1 4 1 3 4 2 ] [ f ( 0 ) f ( 1 ) f ( 2 ) f ( 3 ) ] {\displaystyle {\begin{bmatrix}F(0)\\F(1)\\F(2)\\F(3)\end{bmatrix}}={\begin{bmatrix}1&1&1&1\\1&2&4&3\\1&4&1&4\\1&3&4&2\end{bmatrix}}{\begin{bmatrix}f(0)\\f(1)\\f(2)\\f(3)\end{bmatrix}}}

在一些特殊的情况下，令 F = Z / m {\displaystyle F=Z/m} ，而 m {\displaystyle m} 不是值数也是有意义的。像是 Fermat Number Transform 中 ( m = 2 k + 1 ) {\displaystyle (m=2^{k}+1)} ，以及 Mersenne Number Transform 中 ( m = 2 k − − --> 1 ) {\displaystyle (m=2^{k}-1)} .

参阅

傅里叶级数

傅里叶变换

快速傅里叶变换

数字信号处理

Chirp-Z转换

参考文献

Oppenheim, Alan V.; Schafer, R. W.; and Buck, J. R., (1999). Discrete-time signal processing , Upper Saddle River, N.J. : Prentice Hall. ISBN 0137549202

Mallat, S., A Wavelet Tour of Signal Processing, Second Edition , Academic Press, ISBN 0-12-466606-x

Gill, J., Fourier Transform and Its Applications （[1]）

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。