概述

一个平面切截一个圆锥面得到的椭圆。

椭圆是一种圆锥曲线：如果一个平面切截一个圆锥面，且不与它的底面相交，也不与它的底面平行，则圆锥和平面交截线是个椭圆。

在代数上说，椭圆是在笛卡尔平面上如下形式的方程所定义的曲线

使得 B 2 < 4 A C {\displaystyle B^{2}<4AC\,} ，这里的系数都是实数，并存在定义在椭圆上的点对 (x, y) 的多于一个的解。

穿过两焦点并终止于椭圆上的线段AB 叫做 长轴 。长轴是通过连接椭圆上的两个点所能获得的最长线段。穿过中心（两焦点的连线的中点）垂直于长轴并且终止于椭圆的线段 CD 叫做 短轴 。 半长轴 （图中指示为 a ）是长轴的一半：从中心通过一个焦点到椭圆的边缘的线段。类似的， 半短轴 （图中指示为 b ）是短轴的一半。

如果两个焦点重合，则这个椭圆是圆；换句话说，圆是离心率为零的椭圆。

中心位于原点的椭圆 A x 2 + B x y + C y 2 = 1 {\displaystyle Ax^{2}+Bxy+Cy^{2}=1\,} 可以被看作单位圆在关联于对称矩阵 A ′ ′ --> = [ A B / 2 B / 2 C ] = P D P T {\displaystyle A^{\prime }={\begin{bmatrix}A&B/2\\B/2&C\end{bmatrix}}=PDP^{T}\,} 的线性映射下的图像，这里的 D 是带有 A ′ ′ --> {\displaystyle A^{\prime }} 的特征值的对角矩阵，二者沿着主对角线都是正实数的，而 P 是拥有 A ′ ′ --> {\displaystyle A^{\prime }} 的特征向量作为纵列的实数的酉矩阵。椭圆的长短轴分别沿着 A ′ ′ --> {\displaystyle A^{\prime }} 的两个特征向量的方向，而两个与之对应的特征值分别是 半长轴 和 半短轴 的长度的平方的倒数。

椭圆可以通过对一个圆的所有点的 x 坐标乘以一个常数而不改变 y 坐标来生成。

离心率

椭圆的形状可以用叫做椭圆的离心率的一个数来表达，习惯上指示为 ε ε --> {\displaystyle \varepsilon \,} 。离心率是小于 1 大于等于 0 的正数。离心率 0 表示着两个焦点重合而这个椭圆是圆。

对于有半长轴 a 和半短轴 b 的椭圆，离心率是

离心率越大， a 与 b 的比率就越大，因此椭圆被更加拉长。

半焦距 c 等于从中心到任一焦点的距离，则

距离 c 叫做椭圆的 线性离心率 。在两个焦点间的距离是 2 a ε。

方程

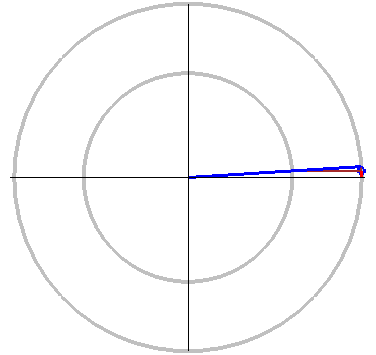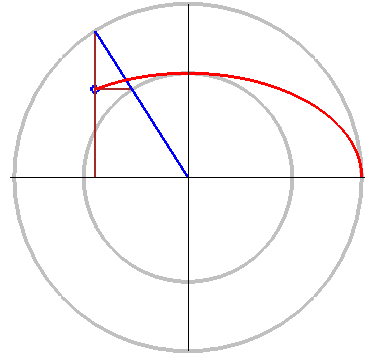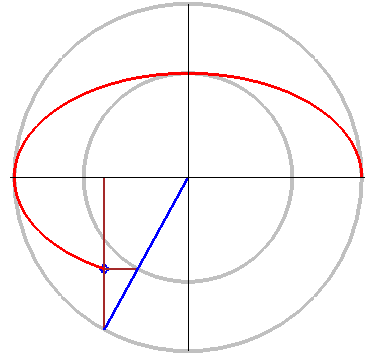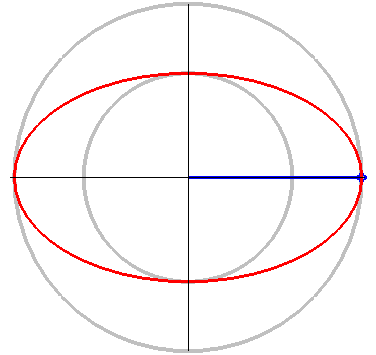
在正规位置上的椭圆的参数方程。参数 t 是蓝线对于 X-轴的角度。

中心位于点 ( h , k ) {\displaystyle (h,k)} 的主轴平行于 x 轴的椭圆由如下方程指定

这个椭圆可以参数化表达为

这里的 t {\displaystyle t} 可以限制于区间 − − --> π π --> ≤ ≤ --> t ≤ ≤ --> π π --> {\displaystyle -\pi \leq t\leq \pi \,\!} 。

如果 h = 0 {\displaystyle h=0} 且 k = 0 {\displaystyle k=0} （就是说，如果中心是原点(0,0))，则

这个参数方程揭示了两个方向相互垂直的简谐运动(表现为具有周期性的简谐波)合成了闭合的椭圆形周期性运动(表现为轨迹是椭圆）。

相对于中心的极坐标形式

用极坐标可表达为

这里的 ε ε --> {\displaystyle \varepsilon } 是椭圆的离心率。

相对于焦点的极坐标形式

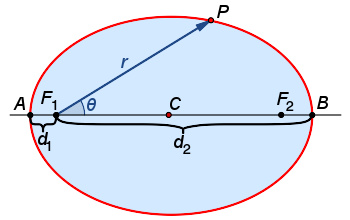
椭圆的极坐标，原点在 F1

有一个焦点在原点的椭圆的极坐标方程是

半正焦弦和极坐标

椭圆的半正焦弦(通常指示为 l {\displaystyle l\,\!} )，是从椭圆的一个焦点到椭圆自身，沿着垂直主轴的直线测量的距离。它有关于 a {\displaystyle a\,\!} 和 b {\displaystyle b\,\!} （椭圆的半轴），通过公式 a l = b 2 {\displaystyle al=b^{2}\,\!} 或者如果使用离心率的话 l = a ⋅ ⋅ --> ( 1 − − --> ε ε --> 2 ) {\displaystyle l=a\cdot (1-\varepsilon ^{2})\,\!} 。

在极坐标中，一个焦点在原点而另一个焦点在负 x 轴上的椭圆给出自方程

椭圆可以被看作是圆的投影：在与水平面有角度 φ 的平面上的圆垂直投影到水平面上给出离心率 sin φ 的椭圆，假定 φ 不是 90°。

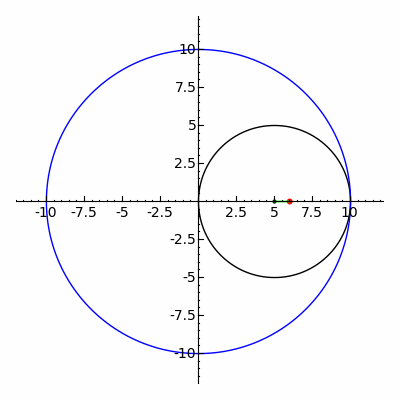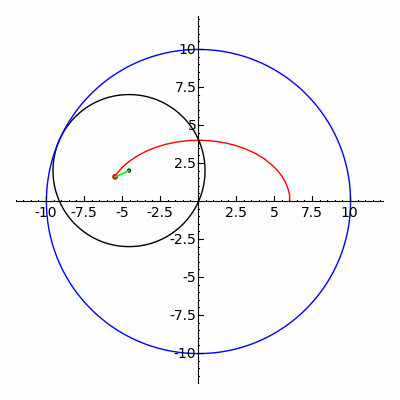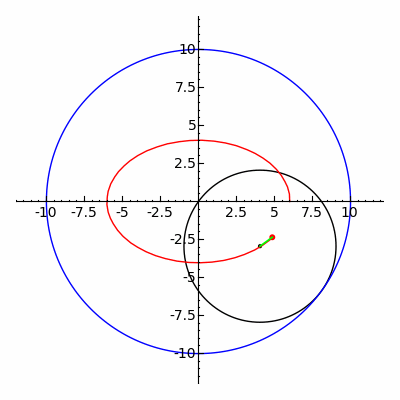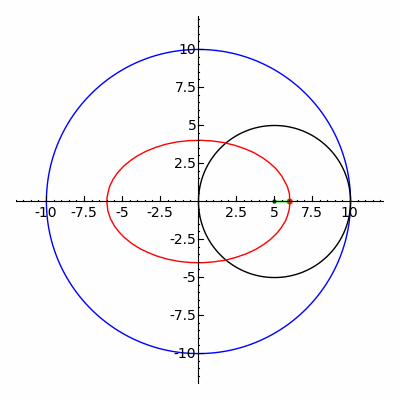
椭圆（用红色绘制）可以表达为内旋轮线在 R=2r 时的特殊情况。

面积和周长

椭圆所包围的面积是 π π --> a b {\displaystyle \pi ab\,} ，这里的 a {\displaystyle a\,} ，和 b {\displaystyle b\,} ， 是半长轴和半短轴。在圆的情况下 a = b {\displaystyle a=b\,} ，表达式简化为 π π --> a 2 {\displaystyle \pi a^{2}\,} 。 椭圆的周长是 4 a E ( c a ) {\displaystyle 4aE({\frac {c}{a}})} ，这里的函数 E {\displaystyle E\,} 椭圆积分完全椭圆积分。

周长为： C = 4 a ∫ ∫ --> 0 π π --> 2 1 − − --> ( c a ) 2 sin 2 ⁡ ⁡ --> θ θ --> d θ θ --> {\displaystyle C=4a\int _{0}^{\frac {\pi }{2}}{\sqrt {1-\left({\frac {c}{a}}\right)^{2}\sin ^{2}\theta }}\ {\rm {d}}\theta \!} 或者 C = 4 a ∫ ∫ --> 0 1 1 − − --> ( c a ) 2 t 2 1 − − --> t 2 d t . {\displaystyle C=4a\int _{0}^{1}{\frac {\sqrt {1-\left({\frac {c}{a}}\right)^{2}t^{2}}}{\sqrt {1-t^{2}}}}\ {\rm {d}}t.\!}

精确的无穷级数为：

或：

拉马努金给出一个更为接近的式子：

它还可以写为：

还有一条近似很高的公式：

标准方程的推导

如果在一个平面内一个 动点 到两个 定点 的距离的和等于定长，那么这个动点的轨迹叫做椭圆。

假设（注意所有假设只是为了导出椭圆方程时比较简便）动点为 P ( x , y ) {\displaystyle P(x,y)\,} ，两个定点为 F 1 ( − − --> c , 0 ) {\displaystyle F_{1}(-c,0)\,} 和 F 2 ( c , 0 ) {\displaystyle F_{2}(c,0)\,} ，则根据定义，动点 P {\displaystyle P} 的轨迹方程满足（定义式）：

用两点的距离公式可得： | P F 1 | = ( x + c ) 2 + y 2 {\displaystyle |PF_{1}|={\sqrt {(x+c)^{2}+y^{2}}}\,} ， | P F 2 | = ( x − − --> c ) 2 + y 2 {\displaystyle |PF_{2}|={\sqrt {(x-c)^{2}+y^{2}}}\,} ，代入定义式中，得：

整理上式，并化简，得：

当 a > c {\displaystyle a>c\,} 时，并设 a 2 − − --> c 2 = b 2 {\displaystyle a^{2}-c^{2}=b^{2}\,} ，则①式可以进一步化简：

因为 a 2 b 2 > 0 {\displaystyle a^{2}b^{2}>0\,} ，将②式两边同除以 a 2 b 2 {\displaystyle a^{2}b^{2}\,} ，可得：

则该方程即动点 P {\displaystyle P} 的轨迹方程，即椭圆的方程。这个形式也是 椭圆的标准方程 。

椭圆的图像如果在直角坐标系中表示，那么上述定义中两个定点被定义在了 x 轴。若将两个定点改在 y 轴，可以用相同方法求出另一个椭圆的标准方程：

在方程中，所设的 2 a {\displaystyle 2a\,} 称为长轴长， 2 b {\displaystyle 2b\,} 称为短轴长，而所设的定点称为焦点，那么 2 c {\displaystyle 2c\,} 称为焦距。在假设的过程中，假设了 a > c {\displaystyle a>c\,} ，如果不这样假设，会发现得不到椭圆。当 a = c {\displaystyle a=c\,} 时，这个动点的轨迹是一个线段；当 a c 2 = b 2 {\displaystyle a^{2}-c^{2}=b^{2}\,} 。

通常认为圆是椭圆的一种特殊情况。

椭圆的旋转和平移

对于平面上任意椭圆 A x 2 + 2 B x y + C y 2 + D x + E y + F = 0 {\displaystyle Ax^{2}+2Bxy+Cy^{2}+Dx+Ey+F=0\,} ，我们总可以将之转化为

的形式。具体步骤为，将后式的各乘积乘方项展开，根据与前式对应项系数相等的法则便可求得u,v,f的值。其中， ( u , v ) {\displaystyle (u,v)\,} 便是该椭圆的中心（f=0）。

若将

带入式中便可得到平移前的椭圆。

若 B ≠ ≠ --> 0 {\displaystyle B\neq 0} ，则表示椭圆的长短轴与坐标系的坐标轴并不平行或垂直，即发生了旋转。设旋转的角度为 φ φ --> {\displaystyle \displaystyle \varphi } ，则有

若将

带入式中便可得到旋转前的椭圆。

渐开线及其导数

有了椭圆渐开线的导数我们可以计算它的长度，其中 E ( t , a 2 − − --> b 2 a ) {\displaystyle E\left(t,{\frac {\sqrt {a^{2}-b^{2}}}{a}}\right)\,} 是第二类完全椭圆积分。

参见

圆锥曲线

开普勒定律

类球面

椭球坐标系

椭圆规

超椭圆

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。