描述

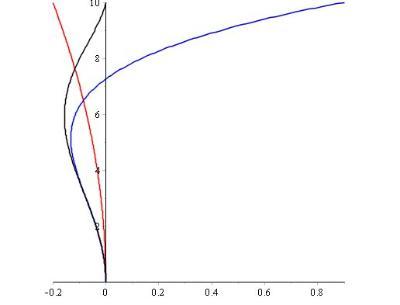
彗形像差是抛物镜望远镜与生俱来的特质，来自于视野中心区域的点光源（像是恒星）可以很好的汇聚在面镜的焦点上（不同于球面镜，来自于镜子周围部分的光线只是接近焦点—球面像差。）。但是，来自于偏离光轴（离轴）方向的光线，自镜子的不同区域反射的光却不能汇聚在相同的焦点上。这样的结果导致不在视野中心的光看起来是楔形的问题，而且离轴越远，这个现象越明显。这使得星点看起来有着彗星的形状，因而得名。在设计上能降低球面像差且没有彗形像差的光学系统有施密特（Schmidt）、马克苏托夫（Maksutov）、和里奇-克莱琴式（ Ritchey-Chrétien ）。

单一透镜或透镜系统的彗形像差，可以经由选择适当的透镜表面曲率有效的降低（某些情况下可以被消除）以合于应用。在单一的波长下，球面像差和彗型像差都最小的透镜称为"最佳形式"或齐明透镜。而目前削减彗形像差最普遍的方法就是使用非球面镜。

薄透镜的彗形像差

薄透镜的彗形像差由下式表示：

彗形像差= h ′ ∗ ∗ --> y 2 ∗ ∗ --> ( − − --> G 5 ∗ ∗ --> c ∗ ∗ --> c 1 + G 7 ∗ ∗ --> c ∗ ∗ --> v 1 + G 8 ∗ ∗ --> c 2 ) {\displaystyle h"*y^{2}*(-G_{5}*c*c_{1}+G_{7}*c*v_{1}+G_{8}*c^{2})}

其中

v 1 {\displaystyle v_{1}} 为物距之倒数。

相关条目

像差

参考文献

^ Rudolf Kingslake, Lens Design Fundamentals p164-165

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。