圆锥曲线的类型

  圆锥曲线的类型：1.抛物线2.圆和椭圆3.双曲线

椭圆，圆：当平面只与圆锥面一侧相交，交截线是闭合曲线的时候，且不过圆锥顶点，结果为椭圆。如果截面与圆锥面的对称轴垂直，结果为圆。

抛物线：截面与圆锥面的母线平行，且不过圆锥顶点，结果为抛物线。

双曲线：截面与圆锥面两侧都相交，且不过圆锥顶点，结果为双曲线。

在平面通过圆锥的顶点的时候，有一些退化情况。交截线可以是一个直线、一个点、或一对直线。

几何性质

椭圆（Ellipse）

椭圆上的点到两个焦点的距离和等于长轴长（2a）。

抛物线（Parabola）

抛物线上的点到焦点的距离等于该点到准线的距离。

双曲线（Hyperbola）

双曲线上的点到两个焦点的距离之差的绝对值等于贯轴长（2a）。

离心率

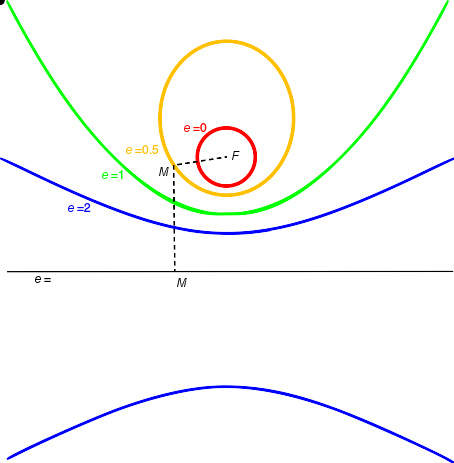
  有固定焦点 F 和准线的 椭圆（ e =1/2） 、 抛物线 ( e =1) 和 双曲线（ e =2） 。

对于椭圆和双曲线，可以采用两种焦点-准线组合，每个都给出同样完整的椭圆或双曲线。从中心到准线的距离是 a / e {\displaystyle a/e\ } ，这里的 a {\displaystyle a\ } 是椭圆的半长轴，或双曲线的半实轴。从中心到焦点的距离是 a e {\displaystyle ae\ } 。

在圆的情况下， e = 0且准线被假想为离中心无限远。这时声称圆由距离是到L的距离的e倍的所有点组成是没有意义的。

圆锥曲线的离心率因此是对它偏离于圆的程度的度量。

对于一个给定的 a {\displaystyle a\ } ， e {\displaystyle e\ } 越接近于1，半短轴就越小。

笛卡尔坐标

在笛卡尔坐标系内，二元二次方程的图像可以表示圆锥曲线，并且所有圆锥曲线都以这种方式引出。方程有如下形式

A x 2 + B x y + C y 2 + D x + E y + F = 0 {\displaystyle Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0\;} 有着参数 A {\displaystyle A\,} ， B {\displaystyle B\,} 和 C {\displaystyle C\,} 不得皆等于 0 {\displaystyle 0\,} 。

如果 B 2 − − --> 4 A C < 0 {\displaystyle B^{2}-4AC<0\,} ，方程表示椭圆（除非圆锥曲线退化了，例如 x 2 + y 2 + 10 = 0 {\displaystyle x^{2}+y^{2}+10=0\,} ）；

如果 A = C {\displaystyle A=C\,} 且 B = 0 {\displaystyle B=0\,} 且 D 2 + E 2 − − --> 4 A F > 0 {\displaystyle D^{2}+E^{2}-4AF>0\,} ,方程表示圆；

如果 B 2 − − --> 4 A C = 0 {\displaystyle B^{2}-4AC=0\,} ，方程表示抛物线；

如果 B 2 − − --> 4 A C > 0 {\displaystyle B^{2}-4AC>0\,} ，方程表示双曲线；

如果还有 A = − − --> C {\displaystyle A=-C\,} ，方程表示直角双曲线。

注意这里的 A {\displaystyle A\,} 和 C {\displaystyle C\,} 就是多项式系数，不是前面定义的半长/短轴的长度。

通过坐标变换这些方程可以变为标准形式：

极坐标

  椭圆的半正焦弦

圆锥曲线的 半正焦弦 （semi-latus rectum）通常指示为 l ，是从单一焦点或两个焦点中的一个，到圆锥曲线自身的，沿着垂直于主轴（长轴）的直线度量的距离。它有关于半长轴 a ，和半短轴 b ，通过公式 a l = b 2 {\displaystyle al=b^{2}\ } 或 l = a ( 1 − − --> e 2 ) {\displaystyle l=a(1-e^{2})\ } 。

在极坐标系中，圆锥曲线有一个焦点在原点，如果有另一个焦点的话它在正 x 轴上，给出自方程

或者，

如上，对于 e = 0得到一个圆，对于0 < e 1得到双曲线。

齐次坐标

在齐次坐标下圆锥曲线可以表示为：

或表示为矩阵：

矩阵 M = [ A 1 B 1 B 2 B 1 A 2 B 3 B 2 B 3 A 3 ] {\displaystyle M={\begin{bmatrix}A_{1}&B_{1}&B_{2}\\B_{1}&A_{2}&B_{3}\\B_{2}&B_{3}&A_{3}\end{bmatrix}}} 叫做“圆锥曲线矩阵”。

Δ Δ --> = d e t ( M ) = | A 1 B 1 B 2 B 1 A 2 B 3 B 2 B 3 A 3 | {\displaystyle \Delta =det(M)={\begin{vmatrix}A_{1}&B_{1}&B_{2}\\B_{1}&A_{2}&B_{3}\\B_{2}&B_{3}&A_{3}\end{vmatrix}}} 叫做圆锥曲线的行列式。如果Δ = 0则这个圆锥曲线被称为退化的，这意味着圆锥曲线是两个直线的联合（两相交直线，两平行直线或两重合直线）或一点。。

例如，圆锥曲线 [ x y z ] . [ 1 0 0 0 − − --> 1 0 0 0 0 ] . [ x y z ] = 0 {\displaystyle {\begin{bmatrix}x&y&z\end{bmatrix}}.{\begin{bmatrix}1&0&0\\0&-1&0\\0&0&0\end{bmatrix}}.{\begin{bmatrix}x\\y\\z\end{bmatrix}}=0} 退化为两相交直线： { x 2 − − --> y 2 = 0 } = { ( x + y ) ( x − − --> y ) = 0 } = { x + y = 0 } ∪ ∪ --> { x − − --> y = 0 } {\displaystyle \{x^{2}-y^{2}=0\}=\{(x+y)(x-y)=0\}=\{x+y=0\}\cup \{x-y=0\}} 。

类似的，圆锥曲线有时退化为两重合直线（两直线重合成一条）: { x 2 + 2 x y + y 2 = 0 } = { ( x + y ) 2 = 0 } = { x + y = 0 } ∪ ∪ --> { x + y = 0 } = { x + y = 0 } {\displaystyle \{x^{2}+2xy+y^{2}=0\}=\{(x+y)^{2}=0\}=\{x+y=0\}\cup \{x+y=0\}=\{x+y=0\}} 。

δ δ --> = | A 1 B 1 B 1 A 2 | {\displaystyle \delta ={\begin{vmatrix}A_{1}&B_{1}\\B_{1}&A_{2}\end{vmatrix}}} 被称为圆锥曲线的判别式。如果δ = 0则圆锥曲线是抛物线，如果δ0则是椭圆。如果δ>0且A 1 = A 2 ，圆锥曲线是圆；如果δ 1的交点，则两个圆锥曲线被称为相切的。如果只共振个四重交点，两个圆锥曲线被称为是共振的。

进一步的，每个直线与每个圆锥曲线相交两次。如果两交点是重合成一点，则这个线被称为切线。因为所有直线交圆锥曲线两次，每个圆锥曲线有两个点在无穷远（与无穷远线的交点）。如果这些点是实数的，圆锥曲线必定是双曲线；如果它们是虚共轭，圆锥曲线必定是椭圆，如果圆锥曲线有双重点在无穷远，则它是抛物线。如果在无穷远的点是 (1,i,0)和（1,-i,0），则圆锥曲线是圆。如果圆锥曲线有一个实数点和一个虚数点在无穷远，或它有两个不共轭的虚数点，它不是抛物线、不是椭圆、不是双曲线。

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。