定义

物体在一段时间 Δ Δ --> t {\displaystyle \Delta t} 内的 速度均速度 v ¯ ¯ --> {\displaystyle {\bar {\boldsymbol {v}}}} 是它在这段时间里的位移 Δ Δ --> r {\displaystyle \Delta {\boldsymbol {r}}} 和时间间隔之比 ：

其中的位移 Δ Δ --> r {\displaystyle \Delta {\boldsymbol {r}}} 是矢量，表示物体的位置 r {\displaystyle {\boldsymbol {r}}} 从开始到结束的变化 。平均速度的大小一般不是物体在这段时间里的平均速率。比如一个以恒定速率做圆周运动一周的物体，由于最后的位置和初始的位置相同，总位移是0，所以平均速度是0，但平均速率不等于0。平均速度总小于等于平均速率。

平均速度是对物体移动快慢和方向的粗略量度，物体在特定时刻运动的快慢和方向则用瞬时速度表示。物体在某一时刻 t 0 {\displaystyle t_{0}} 的 瞬时速度 v ( t 0 ) {\displaystyle {\boldsymbol {v}}(t_{0})} 定义为物体在 t 0 {\displaystyle t_{0}} 左右的很小一段时间 Δ Δ --> t {\displaystyle \Delta t} 中的平均速度在 Δ Δ --> t {\displaystyle \Delta t} 趋向于0时的极限。用数学的语言来说，就是位置矢量 r {\displaystyle {\boldsymbol {r}}} 在 t 0 {\displaystyle t_{0}} 时刻随时间 t {\displaystyle t} 的变化率，也就是对时间的导数 ：

瞬时速度的大小（矢量的模长）等于瞬时速率；瞬时速度的方向则是物体运动曲线的切线方向： v = v e T . {\displaystyle {\boldsymbol {v}}=v{\boldsymbol {e}}_{T}.}

其中 v {\displaystyle v} 是物体在某一点的瞬时速率， e T {\displaystyle {\boldsymbol {e}}_{T}} 是物体运动轨迹曲线在这一点的切向单位矢量 。

例子

直线运动

直线运动是指物体（通常简化成质点）沿着直线运动，当中并无方向的变化。通常会为这个直线指定一个正方向和一个原点，以方便描述。如果物体的速度方向与正方向相同，则记其速度为其速率（正数），反之则记其速度为速率的相反数（负数）。这种记法下，物体的位置、位移和速度都可以用实数来表示。假设物体在初始时刻 t = 0 {\displaystyle t=0} 的位置是 x 0 {\displaystyle x_{0}} ，速度为定值 v {\displaystyle v} ，那么称其做 匀速直线运动 。经过时间 Δ Δ --> t {\displaystyle \Delta t} 以后，物体的位置 x f {\displaystyle x_{f}} 是： x f = x 0 + v Δ Δ --> t {\displaystyle x_{f}=x_{0}+v\Delta t} ，物体的位移是 Δ Δ --> r = v Δ Δ --> t {\displaystyle \Delta {\boldsymbol {r}}=v\Delta t} 。

如果物体的速度随时间均匀改变： v ( t ) = v 0 + a t {\displaystyle v(t)=v_{0}+at} ，那么称之为 匀变速直线运动 。经过时间 Δ Δ --> t {\displaystyle \Delta t} 以后，物体的位置 x f {\displaystyle x_{f}} 是： x f = x 0 + v 0 Δ Δ --> t + 1 2 a Δ Δ --> t 2 {\displaystyle x_{f}=x_{0}+v_{0}\Delta t+{\frac {1}{2}}a\Delta t^{2}} ，物体的位移是 Δ Δ --> r = v 0 Δ Δ --> t + 1 2 a Δ Δ --> t 2 {\displaystyle \Delta {\boldsymbol {r}}=v_{0}\Delta t+{\frac {1}{2}}a\Delta t^{2}} 。

圆周运动

圆周运动是指物体沿圆周做运动。这时候物体的速度是沿圆周切线的方向的矢量。当速度大小恒定时，但方向随时间而变动，即非等速度运动，称为 匀速圆周运动 （其中的“匀速”指“匀速率”）。圆周运动的物体，其平均速度的大小和平均速率是不同的。假设物体以速率 v {\displaystyle v} 做匀速圆周运动，那么它的平均速率永远是 v {\displaystyle v} ，而它的平均速度的大小则是终点和起点构成的弦长度除以间隔的时间。

一般情况下，物体的位移是速度对时间的积分 ： Δ Δ --> r = ∫ ∫ --> 0 Δ Δ --> t v ( t ) d t {\displaystyle \Delta {\boldsymbol {r}}=\int _{0}^{\Delta t}{\boldsymbol {v}}(t)\mathrm {d} t} 。如果物体在初始时刻 t = 0 {\displaystyle t=0} 的位置是 x 0 {\displaystyle {\boldsymbol {x}}_{0}} ，那么经过时间 Δ Δ --> t {\displaystyle \Delta t} 以后，物体的位置 x f {\displaystyle {\boldsymbol {x}}_{f}} 是： x f = x 0 + ∫ ∫ --> 0 Δ Δ --> t v ( t ) d t {\displaystyle {\boldsymbol {x}}_{f}={\boldsymbol {x}}_{0}+\int _{0}^{\Delta t}{\boldsymbol {v}}(t)\mathrm {d} t\,} ，平均速度是： v ¯ ¯ --> = 1 Δ Δ --> t ∫ ∫ --> 0 Δ Δ --> t v ( t ) d t {\displaystyle {\bar {\boldsymbol {v}}}={\frac {1}{\Delta t}}\int _{0}^{\Delta t}{\boldsymbol {v}}(t)\mathrm {d} t}

速度的分解

研究不同的物理问题时，通常会依据研究对象的特性，使用不同的坐标系。在不同的坐标系下，速度有不同的分解方式，选择坐标的方式通常以分解矢量的方便性为主。

直角坐标系

直角坐标系是我们最常用到也最直观的坐标系统如果在三维空间中架设直角坐标系O-xyz，那么一个物体的位置 r {\displaystyle {\boldsymbol {r}}} 可以表示成：

其中 e x , e y , e z {\displaystyle {\boldsymbol {e}}_{x},{\boldsymbol {e}}_{y},{\boldsymbol {e}}_{z}} 分别是x轴、y轴、z轴方向上的单位矢量。物体的速度等于位移对时间的导数 ：

其中 v x , v y , v z {\displaystyle v_{x},v_{y},v_{z}} 是物体速度在三个坐标轴方向上的分量。速度的大小为： | v | = v x 2 + v y 2 + v z 2 {\displaystyle |{\boldsymbol {v}}|={\sqrt {v_{x}^{2}+v_{y}^{2}+v_{z}^{2}}}} 。

极坐标

平面中运动的物体，其速度也可以采用极坐标来表示(依照方便来选择坐标系分解)。极坐标下的速度可以分解为两个部分：径向速度，即物体到原点的距离的变化率，以及角速度，即物体位置的幅角随时间的变化率。假设物体的位置用极坐标表示为 ( r , θ θ --> ) {\displaystyle (r,\theta )} ，定义其径向单位矢量和横向单位矢量为 e r , e θ θ --> {\displaystyle {\boldsymbol {e}}_{r},{\boldsymbol {e}}_{\theta }} ，那么物体的位置矢量可以表示成： r = r e r {\displaystyle {\boldsymbol {r}}=r{\boldsymbol {e}}_{r}} 。

其速度是位移对时间的导数 ：

其中 d r d t e r {\displaystyle {\frac {\mathrm {d} r}{\mathrm {d} t}}{\boldsymbol {e}}_{r}} 称为径向速度， r d θ θ --> d t e θ θ --> {\displaystyle r{\frac {\mathrm {d} \theta }{\mathrm {d} t}}{\boldsymbol {e}}_{\theta }} 称为横向速度 。速度的极坐标描述是依赖于物体位置的描述，因为 e r , e θ θ --> {\displaystyle {\boldsymbol {e}}_{r},{\boldsymbol {e}}_{\theta }} 都是随着物体位置的改变而改变的。物体做圆周运动时， r {\displaystyle r} 是常数，所以径向速度为零，即速度永远沿着圆周切线方向；而横向速度等于 r d θ θ --> d t e θ θ --> {\displaystyle r{\frac {\mathrm {d} \theta }{\mathrm {d} t}}{\boldsymbol {e}}_{\theta }} ，即半径乘以角速度。

如果物体在三维空间中运动，可以加入纵坐标轴z，建立圆柱坐标系： ( ρ ρ --> , θ θ --> , z ) {\displaystyle (\rho ,\theta ,z)} ，物体的位置写作： r = ρ ρ --> e ρ ρ --> + z e z {\displaystyle {\boldsymbol {r}}=\rho {\boldsymbol {e}}_{\rho }+z{\boldsymbol {e}}_{z}} ，其速度为 ：

球坐标

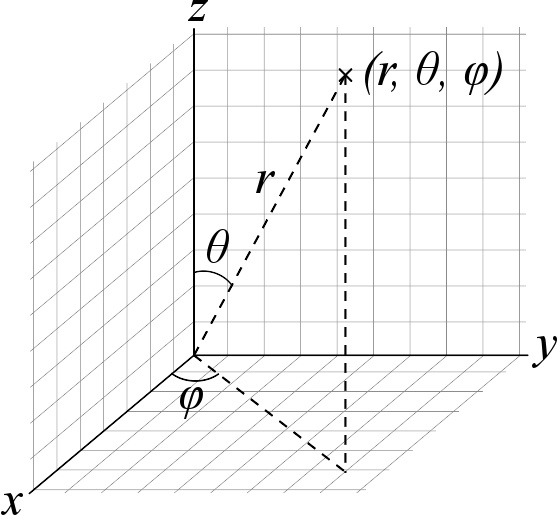
球坐标的表示方式

三维空间中运动的物体，还可以用球坐标系来研究。球坐标系中，物体的速度可以分解成三个部分。除了物体的径向速度外，还有方位角速度和顶角速度，即方位角 φ φ --> {\displaystyle \varphi } 和顶角 θ θ --> {\displaystyle \theta } 的变化率。假设物体的位置用球坐标表示为 ( r , θ θ --> , φ φ --> ) {\displaystyle (r,\theta ,\varphi )} ，定义它的基矢： e r , e θ θ --> , e φ φ --> {\displaystyle {\boldsymbol {e}}_{r},{\boldsymbol {e}}_{\theta },{\boldsymbol {e}}_{\varphi }} ，则物体的位置可以写成： r = r e r . {\displaystyle {\boldsymbol {r}}=r{\boldsymbol {e}}_{r}.}

其速度是位移对时间的导数 ：

自然坐标

如果已知物体运动轨迹，可以使用自然坐标系来描述物体的运动情况。与其他坐标系的不同是，自然坐标系中基矢的选择与物体的运动情况相关。这时候定义的基矢是： e T , e N , e B {\displaystyle {\boldsymbol {e}}_{T},{\boldsymbol {e}}_{N},{\boldsymbol {e}}_{B}} ，分别是切向单位矢量、主法向单位矢量（轨迹曲线在该点的密切圆所在的平面上的法矢量）和副法向单位矢量（与主法向和切矢量垂直的法向矢量）。而物体的速度是沿切向的，所以速度的表达式是：

其中v就是瞬时速率。这是最简洁的坐标表达方式。

相对速度

相对速度是指一个物体相对另一个物体运动的速度。具体来说，假设在某个参考系中，两个物体A和B的速度分别是 v A {\displaystyle {\boldsymbol {v}}_{A}} 和 v B {\displaystyle {\boldsymbol {v}}_{B}} ，那么A相对于B的速度 v A / B {\displaystyle {\boldsymbol {v}}_{A/B}} 就是A在B静止的参考系中的速度。经典物理学中（非相对论框架）， v A / B = v A − − --> v B {\displaystyle {\boldsymbol {v}}_{A/B}={\boldsymbol {v}}_{A}-{\boldsymbol {v}}_{B}\,} ，而B相对于A的速度 v B / A {\displaystyle {\boldsymbol {v}}_{B/A}} 是： v B / A = v B − − --> v A {\displaystyle {\boldsymbol {v}}_{B/A}={\boldsymbol {v}}_{B}-{\boldsymbol {v}}_{A}} 。 ，透过矢量的转换，利用相对速度来解决问题可以将问题简化许多。

经典物理学中的相对速度变换公式是坐标系做伽利略变换的结果。相对论框架中，需要用洛伦兹变换代替伽利略变换，因此相对速度的变换公式也不同。假设物体A的速度是 v = ( v x , v y , v z ) {\displaystyle {\boldsymbol {v}}=(v_{x},v_{y},v_{z})} ，物体B的速度是 u = ( u x , 0 , 0 ) {\displaystyle {\boldsymbol {u}}=(u_{x},0,0)} ，那么物体A相对于物体B的速度是 ：

例如两艘飞船各自以光速 c {\displaystyle c} 的一半朝着相反的方向作直线运动，那么某一艘飞船上的人观察到另一艘飞船的相对速度就是：

相对速度是0.8倍光速，而不是光速 。

参见

四维速度，相对论中的速度表示方式；

速率

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。