面积公式

多边形公式

长方形

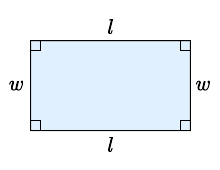
  这个长方形的面积是 lw .

最基本的面积公式是长方形的公式。当 l 是长， w 是宽时，其公式为：

A = l w {\displaystyle A=lw}

当其图形是一个正方形时， l = w {\displaystyle l=w} ，因此正方形的公式为：

A = s 2 {\displaystyle A=s^{2}}

长方形的面积计算方法需要证明。

证明

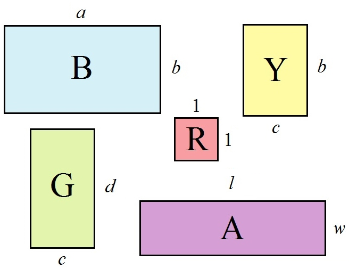
  证明

引理：两个长方形面积之比等于其长宽之积之比

如图，根据《几何原本》第六卷命题一 ——等高之平行四边形的面积比与其底之比等同 ，我们得到

B:Y=a:c

Y:G=b:d

B:G=ab:cd （第五卷命题二十三）

（引理证毕）

定理：长方形的面积等于其长宽之积

根据引理， A:R=lw:(1x1)

定义单位正方形的面积为一平方单位。由于R是单位正方形，因此面积是一平方单位。将一平方单位代入R，得到：A:1=lw:1

（定理证毕）

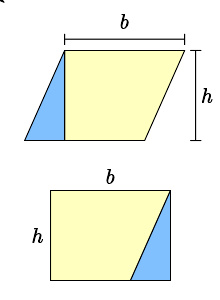
  面积相同

切割图形

有些简单的公式可以切割的方式得出。

例如平行四边形，可以切割成一个梯形和一个直角三角形，如同右图。如果三角形移到平行四边形的另一边，就可以变成一个长方形。因此，平行四边形的面积公式有点像长方形的：

A = b h {\displaystyle A=bh}

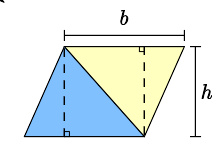
  两个全等三角形

至于同样的平行四边形可以分割为两个全等三角形。因此三角形的公式为：

A = 1 2 b h {\displaystyle A={\frac {1}{2}}bh}

曲线图形面积

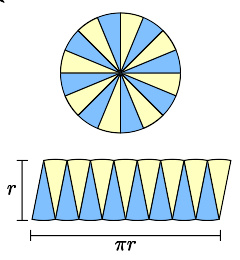
  圆形可以分割为很多扇形

圆形面积公式是基于基本的面积公式，假设有一个半径为r的圆形，分成很多扇形，那一个扇形的面积就会很接近三角形，就像右图一样。如果分得够细小，就可以看到半径为r的圆形面积相等于一个高为r，底为πr的平行四边形。

A = π π --> r 2 {\displaystyle A=\pi r^{2}}

我们也可以用积分得到更肯定为准确的答案

利用三角换元法, 我们代换 x = r sin ⁡ ⁡ --> θ θ --> {\displaystyle x=r\sin \theta }

利用三角恒等式 cos ⁡ ⁡ --> 2 θ θ --> = 2 cos 2 ⁡ ⁡ --> θ θ --> − − --> 1 {\displaystyle \cos 2\theta =2\cos ^{2}\theta \ -1} ，

计算不规则之图形面积，可用填补法或切割法来计算之。

表面积

一些基本的立体 表面积 公式：

立方体： 6 x 2 {\displaystyle 6x^{2}} （ x 是立方体的边长）

长方体： 2 ( l w + w h + h l ) {\displaystyle 2(lw+wh+hl)} （ l 、 w 、 h 分别是长方体的长、宽和高）

球体： 4 π π --> r 2 {\displaystyle 4\pi r^{2}} （ r 是球体的半径）

球冠： 2 π π --> r h {\displaystyle 2\pi rh} （球冠是指被平面截下的部分球面； r 是球体的半径； h 是球冠高）

直立圆锥体： π π --> r ( r + r 2 + h 2 ) {\displaystyle \pi r(r+{\sqrt {r^{2}+h^{2}}})} （ r 是圆锥体底部的半径， h 是它的高）

直立圆柱体： 2 π π --> r ( h + r ) {\displaystyle 2\pi r(h+r)} （ r 是圆柱体圆形底部的半径， h 是它的高）

单位列表

主要单位

面积的测量单位主要包括：

平方米或 平方公尺 ——国际标准单位

公亩（a）——100平方米

公顷（ha）——10,000平方米

平方公里——1,000,000平方米

平方厘米——0.0001平方米

平方毫米——0.01平方厘米

市制：

亩——10丈 × 6丈 ——33.33米 × 20米 ——666.67平方米

平方市里——0.25平方公里

平方市尺——1/9平方米

换算

严格定义

其中一个定义面积的方法是利用公理定义。 面积 可以定义为一个由所有（可测）平面图形组成的集合 M 映射至实数的函数 a ，并满足以下条件：

对于所有 S ∈ ∈ --> M {\displaystyle S\in M} ，有 a ( S ) ≥ ≥ --> 0 {\displaystyle a(S)\geq 0} 。

若 S , T ∈ ∈ --> M {\displaystyle S,T\in M} ，则 S ∪ ∪ --> T ∈ ∈ --> M {\displaystyle S\cup T\in M} 及 S ∩ ∩ --> T ∈ ∈ --> M {\displaystyle S\cap T\in M} ，且 a ( S ∪ ∪ --> T ) = a ( S ) + a ( T ) − − --> a ( S ∩ ∩ --> T ) {\displaystyle a(S\cup T)=a(S)+a(T)-a(S\cap T)} 。

若 S , T ∈ ∈ --> M {\displaystyle S,T\in M} 且 S ⊆ ⊆ --> T {\displaystyle S\subseteq T} ，则 T − − --> S ∈ ∈ --> M {\displaystyle T-S\in M} ，且 a ( T − − --> S ) = a ( T ) − − --> a ( S ) {\displaystyle a(T-S)=a(T)-a(S)} 。

若 S ∈ ∈ --> M {\displaystyle S\in M} 且 S {\displaystyle S} 全等于 T {\displaystyle T} ，则 T ∈ ∈ --> M {\displaystyle T\in M} ，且 a ( S ) = a ( T ) {\displaystyle a(S)=a(T)} 。

任一矩形 R {\displaystyle R} 均属于 M {\displaystyle M} 。若矩形的长为 ℓ ℓ --> {\displaystyle \ell } 而宽为 w {\displaystyle w} ，则 a ( R ) = ℓ ℓ --> w {\displaystyle a(R)=\ell w} 。

设 Q {\displaystyle Q} 为一平面图形。若存在唯一的实数 c {\displaystyle c} ，使得所有满足 S ⊆ ⊆ --> Q ⊆ ⊆ --> T {\displaystyle S\subseteq Q\subseteq T} 的有限个矩形的联集（finite union of rectangles） S {\displaystyle S} 及 T {\displaystyle T} 均有 a ( S ) ≤ ≤ --> c ≤ ≤ --> a ( T ) {\displaystyle a(S)\leq c\leq a(T)} ，则 Q ∈ ∈ --> M {\displaystyle Q\in M} ，且 a ( Q ) = c {\displaystyle a(Q)=c} 。

可以证明，满足上述条件的函数存在。

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。