非线性系统-族谱新闻-族谱网

非线性系统

2020-10-16

出处：族谱网

作者：阿族小谱

浏览:385次

转发:0次

评论:0

定义在数学上，一个线性函数（映射）f(x){displaystylef(x)}拥有以下两个性质：叠加性：f(x+y)=f(x)+f(y){displaystyletextstylef(x+y)=f(x)+f(y)}；齐次：f(αα-->x)=αα-->f(x){displaystyle

定义

在数学上，一个线性函数（映射） f ( x ) {\displaystyle f(x)} 拥有以下两个性质：

叠加性： f ( x + y ) = f ( x ) + f ( y ) {\displaystyle \textstyle f(x+y)\ =f(x)\ +f(y)} ；

齐次： f ( α α --> x ) = α α --> f ( x ) {\displaystyle \textstyle f(\alpha x)\ =\alpha f(x)} 。

在 α 是有理数的情况下，一个可叠加函数必定是齐次函数（在讨论线性与否时，齐次函数专指一次齐次函数）；若 f ( x ) {\displaystyle f(x)} 是连续函数，则只要 α 是任意实数，就可以从叠加性推出齐次。然而在推广至任意复数 α 时，叠加性便再也无法导出齐次了。也就是说，在复数的世界里存在一种反线性映射，它满足叠加性，但却非齐次。叠加性和齐次这两个条件常会被合并在一起，称之为叠加原理：

对于一个表示为

的方程，如果 f ( x ) {\displaystyle f(x)} 是一个线性映射，则称为线性方程，反之则称为非线性方程。另外，如果 C = 0 {\displaystyle C=0} ，则称此方程齐次（齐次在函数和方程上的定义不同，齐次方程指方程内没有和 x 无关的项 C ，即任何项皆和 x 有关）。

这里 f ( x ) = C {\displaystyle f(x)=C} 的定义是很一般性的， x {\displaystyle x} 可为任何数字、矢量、函数等，而 f ( x ) {\displaystyle f(x)} 可以指任意映射，例如有条件限制（给定初始值或边界值）的微分或积分运算。如果 f ( x ) {\displaystyle f(x)} 内含有对 x {\displaystyle x} 的微分运算，此方程即是一个微分方程。

非线性代数方程

代数方程又称为多项式方程。令某多项式等于零可得一个多项式方程，例如：

利用勘根法可以找出某个代数方程的解；但若是代数方程组则较为复杂，有时候甚至很难确定一个代数方程组是否具有复数解（见希尔伯特零点定理）。即使如此，对于一些具有有限个复数解的多项式方程组而言，我们已经找到解的方法，并且也已充分了解这种系统的行为。代数方程组的研究是代数几何里重要的一环，而代数几何正是现代数学里的其中一个分枝。

非线性递回关系

若将一个序列前项和后项之间的关系定义成某个非线性映射，则称为非线性递回关系，例如单峰映射和侯世达数列（英语： Hofstadter sequence ）。由非线性递回关系构成的非线性离散模型，在实际应用中包括 NARMAX（Nonlinear AutoRegressive Moving Average with eXogenous inputs，外部输入非线性自回归移动平均）模型、非线性系统辨识和分析程序等。这些方法可以用来分析时域、频域和时空域（spatio-temporal domains）里复杂的非线。

非线性微分方程

若描述一个系统的微分方程是非线性的，则称此系统为非线性系统。含有非线性微分方程的问题，系统彼此间的表现差异极大，而每个问题的解法或是分析方法也都不一样。非线性微分方程的例子如流体力学的纳维-斯托克斯方程，以及生物学的洛特卡－沃尔泰拉方程。

解非线性问题最大的难处在于找出未知的解：一般来说，我们无法用已知的解来拼凑出其他满足微分方程的未知解；而在线性的系统里，却可以利用一组线性独立的解，透过叠加原理组合出此系统的通解。例如满足狄利克雷边界条件的一维热传导问题，其解（时间的函数）可以写成许多不同频率之正弦函数的线性组合，而这也让它的解很弹性、具有很大的变化空间。通常我们可以找到非线性微分方程的特解，但由于此时叠加原理并不适用，故无法利用这些特解来建构出其他新的解。

常微分方程

一阶常微分方程常常可以利用分离变数法来解，特别是自守方程

例如

这个方程的通解为 u = 1 x + C {\displaystyle u={\frac {1}{x+C}}} ，特解为 u = 0（即通解在 C 趋近于无限大时的极限）。此方程是非线性的，因为它可以被改写为

而等号左边并不是 u 的线性映射。若把此式的 u 换成 u ，则会变成线性方程（指数衰减）。

二阶和高阶非线性常微分方程组的解几乎无法表示成解析解，反而较常表为隐函数或非初等函数积分的形式。

分析常微分方程常用的方法包括：

检查是否有任何守恒量（特别是在处理哈密顿系统的时候）。

检查有没有类似守恒量的耗散量（见李亚普诺夫函数）。

利用泰勒展开式作线性近似。

利用变数变换法，改写成较易分析的方程。

分岔理论。

摄动法（也可应用在代数方程上）。

偏微分方程

研究非线性偏微分方程最常见也最基础的方法就是变数变换，变换以后的方程会较简单，甚至有可能会变成线性方程。有时候，变数变换后的方程可能会变成一个或两个以上的常微分方程（如同用分离变数法解偏微分方程），不管这些常微分方程可不可解，都能帮助我们了解这个系统的行为。

另一个流体力学和热力学里常用的方法（但数学性较低），是利用尺度分析来简化一个较一般性的方程，使它仅适用在某个特定的边界条件上。例如，在描述一个圆管内一维层流的暂态时，我们可以把非线性的纳维-斯托克斯方程简化成一个线性偏微分方程；这时候尺度分析提供了两个特定的边界条件：一维和层流。

其他分析非线性偏微分方程的方法还有特征线法，以及上述分析常微分方程时常用的方法。

单摆

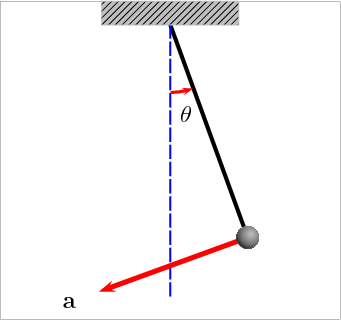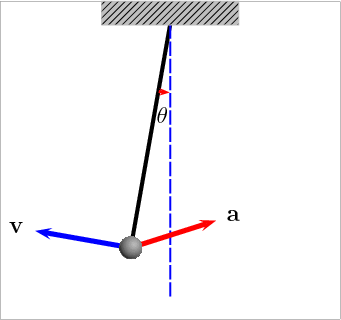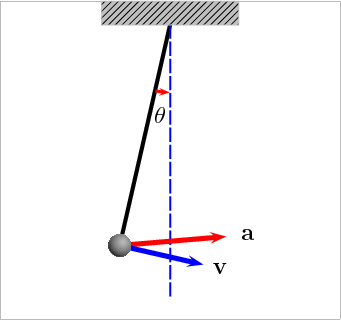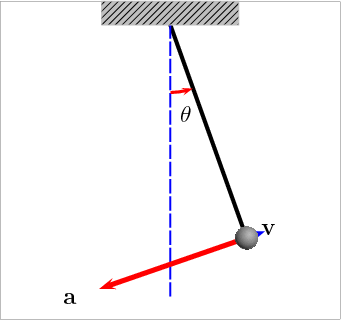
单摆（v 表示速度矢量；a 表示加速度矢量）

非线性问题的一个典型的例子，就是引力作用之下单摆的运动。单摆的运动可由以下的方程来描述（用拉格朗日力学可以证明）：

这是一个非线性且无量纲的方程， θ θ --> {\displaystyle \theta } 是单摆和它静止位置所夹的角度，如动画所示。此方程的一个解法是将 d θ θ --> d t {\displaystyle {\frac {d\theta }{dt}}} 视为积分因子，积分以后得

上述的解是隐解的形式，同时也包含了椭圆积分。这个解通常没有什么用，因为非初等函数积分（即使 C 0 = 0 {\displaystyle C_{0}=0} 仍然是非初等函数）把解的各种特性隐藏了起来，使我们不易看出单摆系统的行为。

另一个解法是把这个非线性方程作线性近似：利用泰勒展开式将非线性的 sine 函数线性化，并在某些特定的点附近讨论解的情形。例如，若在 θ θ --> = 0 {\displaystyle \theta =0} 的点附近作线性近似（又称小角度近似）， θ θ --> ≈ ≈ --> 0 {\displaystyle \theta \approx 0} 时， sin ⁡ ⁡ --> ( θ θ --> ) ≈ ≈ --> θ θ --> {\displaystyle \sin(\theta )\approx \theta } ，故原方程可以改写为

近似后的方程变成了简谐振荡，因此当单摆运动到底部附近时，可以对应到一个简谐振子。而若在 θ θ --> = π π --> {\displaystyle \theta =\pi } （即当单摆运动到圆弧的最高点时）附近作线性近似， sin ⁡ ⁡ --> ( θ θ --> ) = sin ⁡ ⁡ --> ( π π --> − − --> θ θ --> ) ≈ ≈ --> π π --> − − --> θ θ --> {\displaystyle \sin(\theta )=\sin(\pi -\theta )\approx \pi -\theta } ，故原方程可以改写为

这个方程的解含有双曲正弦函数，因此和小角度近似不同，这个近似是不稳定的，也就是说 | θ θ --> | {\displaystyle |\theta |} 会无限制地增加（但此近似方程的解也可能是有界的）。当我们把解对应回单摆系统后，就可以了解为什么单摆在圆弧的最高点时不能达到稳定平衡，也就是说，单摆在最高点时是不稳定的状态。

另一个有趣的线性近似是在 θ θ --> = π π --> 2 {\displaystyle \theta ={\frac {\pi }{2}}} 附近，此时 sin ⁡ ⁡ --> ( θ θ --> ) ≈ ≈ --> 1 {\displaystyle \sin(\theta )\approx 1} ，故原方程可以改写为

这个近似后的方程可以对应到自由落体。

若把以上线性近似的结果合在一起看，就能大致了解单摆的运动情形。利用其他解非线性微分方程的方法，可以进一步帮助我们找到更精确的相图，或是估算单摆的周期。

非线性表现（列举）

经典混沌（和量子混沌相对）—— 指系统里无法预测的行为。

多稳态—— 指系统在两个或多个互斥的状态之间切换。

非周期振荡 —— 指一个函数在任何周期上都不会固定重复其函数值（也称作混沌振荡）。

振幅死亡（英语： Amplitude death ） —— 指系统内的某振荡因系统的自回馈或受其他系统影响而停止的现象。

孤波—— 指行进中能自我增强而不消散的孤立波。

非线性方程（列举）

交流电潮流模型（英语： AC power flow model ）

代数黎卡提方程（英语： Algebraic Riccati equation ）

球杆系统（英语： Ball and beam system ）