分布函数的性质刻划

对于特定的随机变量 X {\displaystyle X} ，其分布函数 F X {\displaystyle F_{X}} 是单调不减及右连续，而且 F X ( − − --> ∞ ∞ --> ) = 0 {\displaystyle F_{X}(-\infty )=0} ， F X ( ∞ ∞ --> ) = 1 {\displaystyle F_{X}(\infty )=1} 。这些性质反过来也描述了所有可能成为分布函数的函数：

设 F : [ − − --> ∞ ∞ --> , ∞ ∞ --> ] → → --> [ 0 , 1 ] , F ( − − --> ∞ ∞ --> ) = 0 , F ( ∞ ∞ --> ) = 1 {\displaystyle F:[-\infty ,\infty ]\to [0,1],F(-\infty )=0,F(\infty )=1} 且单调不减、右连续，则存在概率空间 ( Ω Ω --> , F , P ) {\displaystyle (\Omega ,{\mathcal {F}},\mathbb {P} )} 及其上的随机变量 X ，使得 F 是 X 的分布函数，即 F X = F {\displaystyle F_{X}=F}

随机变量的分布

设 P {\displaystyle P} 为概率测度， X {\displaystyle X} 为随机变量，则函数 F ( x ) = P ( X ≤ ≤ --> x ) {\displaystyle F(x)=P(X\leq x)} ( x ∈ ∈ --> R {\displaystyle x\in \mathbb {R} } ) 称为 X {\displaystyle X} 的概率分布函数。如果将 X {\displaystyle X} 看成是数轴上的随机点的坐标，那么，分布函数 F ( x ) {\displaystyle F(x)} 在 x {\displaystyle x} 处的函数值就表示 X {\displaystyle X} 落在区间 ( − − --> ∞ ∞ --> , x ] {\displaystyle (-\infty ,x]} 上的概率。

例如，设随机变量 X {\displaystyle X} 为掷两次骰子所得的点数差，而整个样本空间由36个元素组成。

其分布函数是：

离散分布

上面所列举的例子属于离散分布，即分布函数的值域是离散的，比如只取整数值的随机变量就是属于离散分布的。 F ( x ) {\displaystyle F(x)} 表示随机变量 X ≤ ≤ --> x {\displaystyle X\leq x} 的概率值。如果 X 的取值只有 x 1 < x 2 < . . . < x n {\displaystyle x_{1} ，则：

F X ( x i ) = ∑ ∑ --> j = 1 i P ( x j ) {\displaystyle F_{X}(x_{i})=\sum _{j=1}^{i}P(x_{j})}

∑ ∑ --> k = 1 n P ( x i ) = 1 {\displaystyle \sum _{k=1}^{n}P(x_{i})=1}

均匀分布

二项分布

二项分布是最重要的离散概率分布之一，由瑞士数学家雅各布·伯努利（Jakob Bernoulli）所发展，一般用二项分布来计算概率的前提是，每次抽出样品后再放回去，并且只能有两种试验结果，比如黑球或红球，正品或次品等。二项分布指出，随机一次试验出现的概率如果为 p {\displaystyle p} ，那么在 n {\displaystyle n} 次试验现 k {\displaystyle k} 次的概率为：

例如，在掷3次骰子中，不出现6点的概率是： f ( 3 , 0 , 1 6 ) = ( 3 0 ) ( 1 6 ) 0 ( 5 6 ) 3 = 0.579 {\displaystyle f(3,0,{\frac {1}{6}})={3 \choose 0}\left({\frac {1}{6}}\right)^{0}\left({\frac {5}{6}}\right)^{3}=0.579} 在连续两次的轮盘游戏中，至少出现一次红色的概率为： f ( 2 , 1 , 18 37 ) + f ( 2 , 2 , 18 37 ) = 0.736 {\displaystyle f(2,1,{\frac {18}{37}})+f(2,2,{\frac {18}{37}})=0.736}

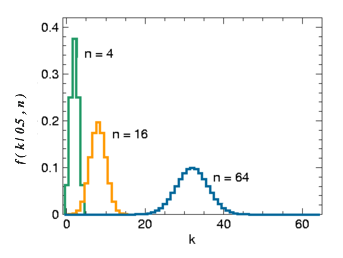
二项分布在 p = 0.5 {\displaystyle p=0.5}

时的对称性 ( 自变量为 k {\displaystyle k}

)

二项分布在 p = 0.5 {\displaystyle p=0.5} 时表现出图像的对称性，而在 p {\displaystyle p} 取其它值时是非对称的。另外二项分布的期望值 E ⁡ ⁡ --> ( X ) = n p {\displaystyle \operatorname {E} (X)=np} ，以及方差 var ⁡ ⁡ --> ( X ) = n p ( 1 − − --> p ) {\displaystyle \operatorname {var} (X)=n\,p\,(1-p)\!}

正态分布

几何分布

超几何分布

作为离散概率分布的超几何分布尤其指在抽样试验时抽出的样品不再放回去的分布情况。在一个容器中一共有 N {\displaystyle N} 个球，其中 M {\displaystyle M} 个黑球， ( N − − --> M ) {\displaystyle (N-M)} 个红球，通过下面的超几何分布公式可以计算出，从容器中抽出的 n {\displaystyle n} 个球中（抽出的球不放回去）有 k {\displaystyle k} 个黑球的概率是多少：

例如，容器中一共10个球，其中6个黑色，4个白色，一共抽5次（抽出的球不放回去），在这5个球中有3个黑球的概率是： f ( k = 3 ) = ( 6 3 ) ( 10 − − --> 6 5 − − --> 3 ) ( 10 5 ) = 0.476 {\displaystyle f(k=3)={\frac {\displaystyle {6 \choose 3}{10-6 \choose 5-3}}{\displaystyle {10 \choose 5}}}=0.476}

超几何分布和二项分布的关系

和二项分布不同的是，在超几何分布中，特别强调的是抽出的样品在下一次抽取前不再放回去，但是如果抽取的次数 n {\displaystyle n} 和总共样品数 N {\displaystyle N} 相比很小（大约 n / N < 0 , 05 {\displaystyle n/N<0,05} ），这时在计算上二项分布和超几何分布相互间则没有主要的区别，此时人们更愿意采用二项分布的方法，因为在数学计算上二项分布要简单一些。

泊松近似

泊松近似是二项分布的一种极限形式。其强调如下的试验前提：一次抽样的概率值 p {\displaystyle p} 相对很小，而抽取次数 n {\displaystyle n} 值又相对很大。因此泊松分布又被称之为罕有事件分布。泊松分布指出，如果随机一次试验出现的概率为 p {\displaystyle p} ，那么在 n {\displaystyle n} 次试验现 k {\displaystyle k} 次的概率按照泊松分布应该为：

其中数学常数 e = 2.71828... {\displaystyle e=2.71828...} (自然对数的底数) 例如，某工厂在生产零件时，每200个成品中会有1个次品，那么在100个零件中最多出现2个次品的概率按照泊松分布应该是： f ( 100 , 0 , 1 200 ) + f ( 100 , 1 , 1 200 ) + f ( 100 , 2 , 1 200 ) = 0.986 {\displaystyle f(100,0,{\frac {1}{200}})+f(100,1,{\frac {1}{200}})+f(100,2,{\frac {1}{200}})=0.986}

在实践中如果遇到 n {\displaystyle n} 值很大导致二项分布难于计算时，可以考虑使用泊松分布，但前提是 n ⋅ ⋅ --> p {\displaystyle n\cdot p} 必须趋于一个有限极限。 采用泊松分布的一个不太严格的规则（通过展开二项分布，并在形式上化简为类似泊松分布后，利用极限化简即可得） 是：

n ≥ ≥ --> 100 {\displaystyle n\geq 100}

p ≤ ≤ --> 0.1 {\displaystyle p\leq 0.1}

连续分布

设 X {\displaystyle X} 是具有分布函数 F {\displaystyle F} 的连续随机变量，且 F 的一阶导数处处存在，则其导函数

称为 X {\displaystyle X} 的概率密度函数。 每个概率密度函数都有如下性质：

∫ ∫ --> − − --> ∞ ∞ --> ∞ ∞ --> f ( x ) d x = 1 {\displaystyle \int _{-\infty }^{\infty }f(x)\,{\rm {d}}x=1}

∫ ∫ --> a b f ( x ) d x = P ⁡ ⁡ --> ( a ≤ ≤ --> X ≤ ≤ --> b ) = F ( b ) − − --> F ( a ) {\displaystyle \int _{a}^{b}f(x)\,{\rm {d}}x=\operatorname {P} (a\leq X\leq b)=F(b)-F(a)}

第一个性质表明，概率密度函数与 x {\displaystyle x} 轴形成的区域的面积等于1，第二个性质表明，连续随机变量在区间 [ a , b ] {\displaystyle [a,b]} 的概率值等于密度函数在区间 [ a , b ] {\displaystyle [a,b]} 上的积分，也即是与 X {\displaystyle X} 轴在 [ a , b ] {\displaystyle [a,b]} 内形成的区域的面积。因为 0 ≤ ≤ --> F ( x ) ≤ ≤ --> 1 {\displaystyle 0\leq F(x)\leq 1} ，且 f ( x ) {\displaystyle f(x)} 是 F ( x ) {\displaystyle F(x)} 的导数，因此按照积分原理不难推出上面两个公式。

正态分布、指数分布、 t {\displaystyle t} -分布， F {\displaystyle F} -分布以及 Ξ Ξ --> 2 {\displaystyle \Xi ^{2}} -分布都是连续分布。

均匀分布

指数分布

伽马分布

正态分布

连续随机变量的概率密度函数如果是如下形式，

那么这个连续分布被称之为正态分布，或者高斯分布。其密度函数的曲线呈对称钟形，因此又被称之为钟形曲线，其中 μ μ --> {\displaystyle \mu } 是平均值， σ σ --> {\displaystyle \sigm标准差 是标准差。正态分布是一种理想分布，许多典型的分布，比如成年人的身高，汽车轮胎的运转状态，人类的智商值（IQ），都属于或者说至少接近正态分布。同样按照连续分布的定义，正态概率密度函数具有和普通概率密度函数类似的性质：

∫ ∫ --> − − --> ∞ ∞ --> ∞ ∞ --> f ( t ) d t = 1 {\displaystyle \int _{-\infty }^{\infty }f(t)\,{\rm {d}}t=1}

F ( x ) = 1 σ σ --> 2 π π --> ∫ ∫ --> − − --> ∞ ∞ --> x e ( − − --> 1 2 ( t − − --> μ μ --> σ σ --> ) 2 ) d t {\displaystyle F(x)={\frac {1}{\sigma {\sqrt {2\pi }}}}\int _{-\infty }^{x}e^{\left(-{\frac {1}{2}}\left({\frac {t-\mu }{\sigma }}\right)^{2}\right)}\,{\rm {d}}t}

如果给出一个正态分布的平均值 μ μ --> {\displaystyle \mu } 以及标准差 σ σ --> {\displaystyle \sigma } ，可以根据上面的第二个公式计算出任一区间的概率分布情况。但是如上的计算量是相当庞大的，没有计算机的辅助基本是不可能的，解决这一问题的方法是借助 z {\displaystyle z} -变换以及标准正态分布表格（ z {\displaystyle z} -表格）。

中间值 μ μ --> = 0 {\displaystyle \mu =0} 以及标准差 σ σ --> = 1 {\displaystyle \sigma =1} 的正态分布被称之为标准正态分布，其累积分布函数是

File:Z-transformation.png z {\displaystyle z} -变换示意图

将普通形式的正态分布变换到标准正态分布的方法是

例如，已知一正态分布的 μ μ --> = 5 {\displaystyle \mu =5} ， σ σ --> = 3 {\displaystyle \sigma =3} ，求区间概率值 P ( 4 7 ) ? {\displaystyle P(4 计算过程如下，

其中 Φ Φ --> ( z ) {\displaystyle \Phi (z)} 值通过查 z {\displaystyle z} -表格获得。

正态分布和二项分布

在离散分布中如果试验次数 n {\displaystyle n} 值非常大，而且单次试验的概率 p {\displaystyle p} 值又不是很小的情况下，正态分布可以用来近似的代替二项分布。一个粗略的使用正态分布的近似规则是： n ⋅ ⋅ --> p ⋅ ⋅ --> ( 1 − − --> p ) ≥ ≥ --> 9 {\displaystyle n\cdot p\cdot (1-p)\geq 9} 。 从二项分布中获得 μ μ --> {\displaystyle \mu } 和 σ σ --> {\displaystyle \sigma } 值的方法是

期望值 μ μ --> = n ⋅ ⋅ --> p {\displaystyle \mu =n\cdot p}

标准差 σ σ --> = n ⋅ ⋅ --> p ⋅ ⋅ --> ( 1 − − --> p ) {\displaystyle \sigma ={\sqrt {n\cdot p\cdot (1-p)}}}

如果 σ σ --> > 3 {\displaystyle \sigma >3} ，则必须采用下面的近似修正方法：

( 注： q = 1 − − --> p {\displaystyle q=1-p} , EF：二项分布，ZF：正态分布)

上（下）临界值分别增加（减少）修正值0.5的目的是在 σ σ --> {\displaystyle \sigma } 值很大时获得更精确的近似值，只有 σ σ --> {\displaystyle \sigma } 很小时，修正值0.5可以不被考虑。

例如，随机试验为连续64次掷硬币，获得的国徽数位于32和42之间的概率是多少？用正态分布计算如下，

n ⋅ ⋅ --> p ⋅ ⋅ --> q = 16 ≥ ≥ --> 9 {\displaystyle n\cdot p\cdot q=16\geq 9} ，符合近似规则，应用 z {\displaystyle z} -变换：

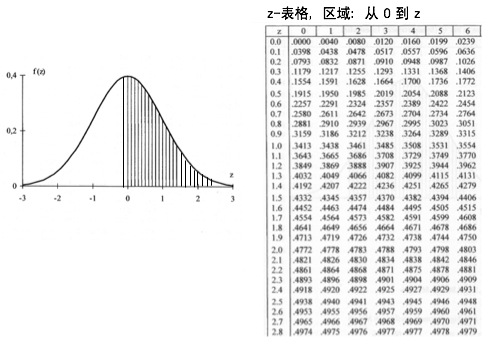
标准正态分布 N ( 0 , 1 ) {\displaystyle N(0,1)}

下的 z {\displaystyle z}

-表格

在运用 z {\displaystyle z} - 表格时注意到利用密度函数的对称性来求出 z {\displaystyle z} 为负值时的区域面积。

参考文献

（德文） 彼得 缺菲尔（Peter Zoefel）：《统计和经济学家》PEASON Studium出版社2003年ISBN 3-8273-7062-0

（德文） 约瑟夫 西拉（Josef Schira）：《统计理论与企业管理》PEASON Studium出版社2003年ISBN 3-8273-7041-8

（德文） 汉斯－底特 黑伯曼（Hans-Dieter Hippmann）：《统计学》SCHAEFFER POESCHEL出版社2003年ISBN 3-7910-2119-2

参见

概率论

随机变数

累积分布函数

概率密度函数

概率质量函数

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。