物理动机

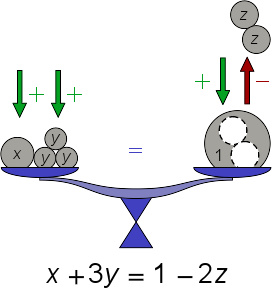
一维热方程图解（观看动画版）

热传导在三维的等方向均匀介质里的传播可用以下方程表达：

其中：

u =u(t, x, y, z)表温度，它是时间变数t与空间变数(x,y,z)的函数。

∂ ∂ --> u {\displaystyle {\partial u}} / ∂ ∂ --> t {\displaystyle {\partial t}} 是空间中一点的温度对时间的变化率。

u x x {\displaystyle u_{xx}} , u y y {\displaystyle u_{yy}} 与 u z z {\displaystyle u_{zz}} 温度对三个空间坐标轴的二次导数。

k是热扩散率，决定于材料的热传导率、密度与热容。

热方程是傅里叶冷却律的一个推论（详见条目热传导）。

如果考虑的介质不是整个空间，则为了得到方程的唯一解，必须指定u的边界条件。如果介质是整个空间，为了得到唯一性，必须假定解的增长速度有个指数型的上界，此假定吻合实验结果。

热方程的解具有将初始温度平滑化的特质，这代表热从高温处向低温处传播。一般而言，许多不同的初始状态会趋向同一个稳态（热平衡）。因此我们很难从现存的热分布反解初始状态，即使对极短的时间间隔也一样。

热方程也是抛物线偏微分方程最简单的例子。

利用拉普拉斯算子，热方程可推广为下述形式

其中的 Δ Δ --> {\displaystyle \Delta } 是对空间变数的拉普拉斯算子。

热方程支配热传导及其它扩散过程，诸如粒子扩散或神经细胞的动作电势。热方程也可以作为某些金融现象的模型，诸如布莱克-斯科尔斯模型与Ornstein-Uhlenbeck过程。热方程及其非线性的推广型式也被应用于影像分析。量子力学中的薛定谔方程虽然有类似热方程的数学式（但时间参数为纯虚数），本质却不是扩散问题，解的定也完全不同。

就技术上来说，热方程违背狭义相对论，因为它的解表达了一个扰动可以在瞬间传播至空间各处。扰动在前方光锥外的影响通常可忽略不计，但是若要为热传导推出一个合理的速度，则须转而考虑一个双曲线型偏微分方程。

以傅里叶级数解热方程

  在理想状态下一根棍子的热传导，配上均匀的边界条件。

以下解法首先由约瑟夫·傅里叶在他于1822年出版的著作Théorie analytique de la chaleur（中译：解析热学）给出。先考虑只有一个空间变数的热方程，这可以当作棍子的热传导之模型。方程如下：

其中u = u(t, x)是t和x的双变数函数。

x是空间变数，所以x ∈ [0,L]，其中L表示棍子长度。

t是时间变数，所以t ≥ 0。

假设下述初始条件

其中函数f是给定的。再配合下述边界条件

让我们试着找一个非恒等于零的解，使之满足边界条件(3)并具备以下形式：

这套技术称作分离变数法。现在将u代回方程(1)，

由于等式右边只依赖x，而左边只依赖t，两边都等于某个常数− λ，于是：

以下将证明(6)没有λ ≤ 0的解：

假设λ < 0，则存在实数B、C使得

从(3)得到

于是有B = 0 = C，这蕴含u恒等于零。

假设λ = 0，则存在实数B、C使得

仿上述办法可从等式(3)推出u恒等于零。

因此必然有λ > 0，此时存在实数A、B、C使得

从等式(3)可知C = 0，因此存在正整数n使得

由此得到热方程形如(4)的解。

一般而言，满足(1)与(3)的解相加后仍是满足(1)与(3)的解。事实上可以证明满足(1)、(2)、(3)的解由下述公式给出：

其中

推广求解技巧

上面采用的方法可以推广到许多不同方程。想法是：在适当的函数空间上，算子 u ↦ ↦ --> u x x {\displaystyle u\mapsto u_{xx}} 可以用它的特征矢量表示。这就自然地导向线性自伴算子的谱理论。

考虑线性算子Δ u = ux x，以下函数序列

是Δ的特征矢量。诚然：

此外，任何满足边界条件f(0)=f(L)=0的Δ的特征矢量都是某个en。令L(0, L)表 [0, L]上全体平方可积函数的矢量空间。这些函数en构成L(0, L)的一组正交归一基。更明白地说：

最后，序列{en}n ∈ N张出L(0, L)的一个稠密的线性子空间。这就表明我们实际上已将算子Δ对角化。

非均匀不等向介质中的热传导

一般而言，热传导的研究奠基于以下几个原理。首先注意到热流是能量流的一种形式，因此可以谈论单位时间内流进空间中一块区域的热量。

单位时间内流入区域 V的热量由一个依赖于时间的量qt(V)给出。假设q有个密度Q(t,x)，于是

热流是个依赖于时间的矢量函数H(x)，其刻划如下：单位时间内流经一个面积为dS而单位法矢量为n的无穷小曲面元素的热量是

因此单位时间内进入V的热流量也由以下的面积分给出

其中n(x)是在x点的向外单位法矢量。

热传导定律说明温度对时间的梯度满足以下线性关系

利用格林定理可将之前的面积分转成一个体积分

温度在x点对时间的改变率与流进x点所在的无穷小区域的热量成正比，此比例常数与时间无关，而可能与空间有关，写作κ(x)。

将以上所有等式合并，便获得支配热流的一般公式。

注记：

系数κ(x)是该材料在x点的密度和比热的积的倒数。

在等方向性介质的情况，矩阵A只是个标量，等于材料的导热率。

在非等向的情况，A不一定是标量，我们鲜少能明确写出热方程的解。然而通常可考虑相应的抽象柯西问题，证明它是适定的，并（或）导出若干定性结果（诸如初始值保持正性、无穷传播速度、收敛至平衡态或一些平滑化性质）。这些论证通常有赖于单参数半群理论：举例来说，如果A是个对称矩阵，那么由

粒子扩散

粒子扩散方程

在粒子扩散的模型中，我们考虑的方程涉及

在大量粒子集体扩散的情况：粒子的体积浓度，记作c。或者

在单一粒子的情况：单一粒子对位置的概率密度函数，记作P。

不同情况下的方程：

或者

c与P都是位置与时间的函数。D是扩散系数，它控制扩散速度，通常以米/秒为单位。

如果扩散系数D依赖于浓度c（或第二种情况下的概率密度P），则我们得到非线性扩散方程。

单一粒子在粒子扩散方程下的随机轨迹是个布朗运动。

如果一个粒子在时间 t = 0 {\displaystyle t=0} 时置于 R → → --> = 0 → → --> {\displaystyle {\vec {R}}={\vec {0}}} ，则相应的概率密度函数具有以下形式：

它与概率密度函数的各分量 R x {\displaystyle R_{x}} 、 R y {\displaystyle R_{y}} 和 R z {\displaystyle R_{z}} 的关系是：

随机变数 R x , R y , R z {\displaystyle R_{x},R_{y},R_{z}} 服从平均数为0、变异数为 2 D t {\displaystyle 2\,D\,t} 的正态分布。在三维的情形，随机矢量 R → → --> {\displaystyle {\vec {R}}} 服从平均数为 0 → → --> {\displaystyle {\vec {0}}} 、变异数为 6 D t {\displaystyle 6\,D\,t} 的正态分布。

在t=0时，上述 P ( R → → --> , t ) {\displaystyle P({\vec {R}},t)} 的表示式带有奇点。对应于粒子处在原点之初始条件，其概率密度函数是在原点的狄拉克δ函数，记为 δ δ --> ( R → → --> ) {\displaystyle \delta ({\vec {R}})} （三维的推广是 δ δ --> ( R → → --> ) = δ δ --> ( R x ) δ δ --> ( R y ) δ δ --> ( R z ) {\displaystyle \delta ({\vec {R}})=\delta (R_{x})\delta (R_{y})\delta (R_{z})} ）；扩散方程对此初始值的解也称作格林函数。

扩散方程的历史源流

粒子扩散方程首先由Adolf Fick于1855年导得。

以格林函数解扩散方程

格林函数是扩散方程在粒子位置已知时的解（数学家称之为扩散方程的基本解）。当粒子初始位置在原点 0 → → --> {\displaystyle {\vec {0}}} 时，相应的格林函数记作 G ( R → → --> , t ) {\displaystyle G({\vec {R}},t)} （t>0）；根据扩散方程对平移的对称性，对一般的已知初始位置 R → → --> 0 {\displaystyle {\vec {R}}^{0}} ，相应的格林函数是 G ( R → → --> − − --> R → → --> 0 , t ) {\displaystyle G({\vec {R}}-{\vec {R}}^{0},t)} 。

对于一般的初始条件，扩散方程的解可以透过积分分解为一族格林函数的叠加。

举例来说，设t=0时有一大群粒子，根据浓度分布的初始值 c ( R → → --> , 0 ) {\displaystyle c({\vec {R}},0)} 分布于空间中。扩散方程的解将告诉我们浓度分布如何随时间演化。

跟任何（广义）函数一样，浓度分布的初始值可以透过积分表为狄拉克δ函数的叠加：

扩散方程是线性的，因此在之后的任一时刻t，浓度分布变为：

在粒子扩散的情形，我们可以将狄拉克δ函数对应的初始条件理解为粒子落在一个已知位置。一般而言，任何扩散过程的解都有这种表法，包括热传导或动量的扩散；后者关系到流体的黏性现象。

一维格林函数解列表

以下以简写BC代表边界条件，IC代表初始条件。

（可能的问题：根据上解，u(0)=0）

应用

热方程在许多现象的数学模型现，而且常在金融数学中作为期权的模型出现。著名的布莱克-斯科尔斯模型中的差分方程可以转成热方程，并从此导出较简单的解。许多简单期权的延伸模型没有解析解，因此必须以数值方法计算模型给出的定价。热方程可以用Crank-Nicolson法有效地求数值解，此方法也可用于许多无解析解的模型（详见文献Wilmott，1995）。

热方程在流形上的推广是处理阿蒂亚-辛格指标定理的主要工具之一，由此也导向热方程在黎曼几何中有许多应用。

参见

热

偏微分方程

发展方程

文献

Einstein, A. "Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen." Ann. Phys. 17, 549, 1905.[1]

Wilmott P., Howison S., Dewynne J. (1995)The Mathematics of Financial Derivatives:A Student Introduction. Cambridge University Press.

L.C. Evans, Partial Differential Equations, American Mathematical Society, Providence, 1998. ISBN 0-8218-0772-2.

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。