历史

关于滑轮的绘品最早出现于一幅公元前八世纪的亚述浮雕。这浮雕展示的是一种非常简单的滑轮，只能改变施力方向，主要目的是为了方便施力，并不会给出任何机械利益。在中国，滑轮装置的绘制最早出现于汉代的画像砖、陶井模。 在《墨经》里也有记载关于滑轮的论述。

古希腊人将滑轮归类为简单机械。 早在公元前400年，古希腊人就已经知道如何使用复式滑轮了。大约在公元前330年，亚里斯托德在著作《机械问题》（《Mechanical Problems》）里的第十八个问题，专门研讨“复式滑轮”系统。 阿基米德贡献出很多关于简单机械的知识，详细地解释滑轮的运动学理论。 据说阿基米德曾经独自使用复式滑轮拉动一艘装满了货物与乘客的大海船。 西元一世纪，亚历山大的希罗分析并且写出关于复式滑轮的理论，证明了负载与施力的比例等于承担负载的绳索段的数目，即“滑轮原理”。

1608年，在著作《数学纪要》（《Mathematical Collection》）里，荷兰物理学者西蒙·斯特芬表明，滑轮系统的施力与负载之间移动路径的长度比率，等于施力与负载之间的反比率。这是雏型的虚功原理。

1788年，法国物理学者约瑟夫·拉格朗日在钜著《分析力学》（《Mécanique analytique》）里，使用滑轮原理推导出虚功原理，从而揭起了拉格朗日力学的序幕。

操作理论

为了简易分析起见，假设滑轮和绳索的重量为零，不会因摩擦而损失任何能量，绳索也不会被延伸拉长。

定滑轮

定滑轮的中心轴固定不动。定滑轮的功能是改变力的方向。当牵拉重物时，可使用定滑轮将施力方向转变为容易出力的方向。使用定滑轮时，施力牵拉的距离等于物体上升的距离，不能省力也不费力。绳索两端的拉力相等，所以，输出力等于输入力，定滑轮的机械利益等于1。

动滑轮

动滑轮的中心轴可以移动。动滑轮不能改变施力方向。在静力平衡时，作用于滑轮的净力必需等于零。另外，绳索两端的拉力相等。所以，在绳索每一端的拉力等于负载的一半。假设，将绳索的一端系绑于一固定点，则用拉力 W / 2 {\displaystyle W/2} 于绳索的另一端，就可以提升负载 W {\displaystyle W} 。若要把负载提升高度 h {\displaystyle h} ，则必须在绳子的自由端往上方拉动 2 h {\displaystyle 2h} 的距离。

滑车组

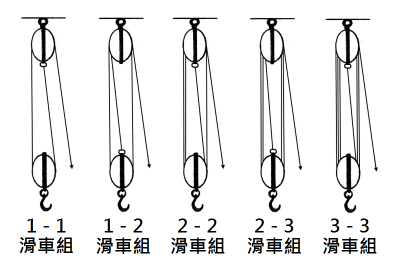
由定滑车与动滑车以绳索缠绕牵引组成的各种各样的滑车组。

定义“滑车”为一组中心轴同轴的滑轮。按照滑轮数目不同，滑车可以分为单门滑车、双门滑车和多门滑车。按滑车中心轴的位置是否移动，可将滑车分为“定滑车”、“动滑车”：定滑车的中心轴固定不动，动滑车的中心轴可以移动。如右图所示，滑车组是由定滑车与动滑车以绳索穿绕组成， 定滑车悬挂于上方的固定点，动滑轮吊挂着下方的负载。绳索穿绕的方法有几种。绳索被系缚的一端称为“终结端”，可以系缚于定滑车或动滑车；另一端称为“自由端”，是施力处。

滑车组的机械利益等于承担动滑轮与其负载的绳子数目。在右图中的各种各样滑车组的机械利益分别为

1－1滑车组（单门动滑车，单门定滑车，定端头固定于定滑车）：2

1－2滑车组（单门动滑车，双门定滑车，定端头固定于动滑车）：3

2－2滑车组（双门动滑车，双门定滑车，定端头固定于定滑车）：4

2－3滑车组（双门动滑车，三门定滑车，定端头固定于动滑车）：5

3－3滑车组（三门动滑车，三门定滑车，定端头固定于定滑车）：6

滑车组的特性是使用单独一条绳索来传输张力，通过一个或多个滑轮，达成提升或移动负载的目的。假设绳索的质量为零，则绳索的任意位置所感受到的张力都一样。假设滑车组系统不耗散或储存能量，则其机械利益等于作用于负载的拉力的数目。计算这数目很简单。首先，滑车组的每一个滑轮只能有一条绳索缠绕于其凹槽，这可以当作从滑轮引出两条绳索段。另外，终结端被系缚的滑车，可当作从滑车引出一条绳索段。由于每一条绳索段都是同样绳索的一部分，承担负载的每一条绳索段都会施加同样的拉力于负载，所以，机械利益等于从负载引出的绳索段的数目。

假设一个滑车所吊挂的负载为 W {\displaystyle W} ，从这滑车引出的绳索段数目为 p {\displaystyle p} ，则在静力平衡下，每一条绳索段的拉力为 W / p {\displaystyle W/p} ，这意味着输入力为 W / p {\displaystyle W/p} 。因此，这滑车组能够减少输入力的因子为 p {\displaystyle p} ，机械利益为 p {\displaystyle p} 。

1－1滑车组

如左图所示，左边是1－1滑车组绘图，右边是将滑车组的滑轮分离后的受力简图。对于1－1滑车组，下方动滑车吊挂的负载为 W {\displaystyle W} ，从这动滑车引出的绳索段数目为 2 {\displaystyle 2} ，所以输入力为 W / 2 {\displaystyle W/2} ，机械利益为 2 {\displaystyle 2} 。

注意到左边1－1滑车组绘图并不很正确，从终结端到动滑轮的绳索段不呈垂直方向，因此其牵拉动滑轮的拉力具有水平分量，由于没有其它作用力能够抵消这水平拉力，所以这滑车组不处于静力平衡，动滑轮会往旁边移动，使得水平拉力能被抵消。这瑕疵所造成的误差不大，可以被忽略，前面所做数值分析大约正确。

2－2滑车组

如左图所示，左边是2－2滑车组绘图，右边是将滑车组的滑轮分离后的受力简图。对于2－2滑车组，下方动滑车吊挂的负载为 W {\displaystyle W} ，从这动滑车引出的绳索段数目为 4 {\displaystyle 4} ，所以输入力为 W / 4 {\displaystyle W/4} ，机械利益为 4 {\displaystyle 4} 。

注意到左边2－2滑车组绘图并不很正确，详尽细节请参阅先前1－1滑车组段落。

1－1滑车组逆反版

假设将1－1滑车组的绳索缠绕穿引方式逆反，并将终结端系缚至动滑车，让自由端的施力方向与负载重量的方向相反，则可以增加滑车组的机械利益。如左图所示，从动滑车引出的绳索段数目为 3 {\displaystyle 3} ，所以输入力为 W / 3 {\displaystyle W/3} ，机械利益为 3 {\displaystyle 3} 。

2－1滑车组

假设将1－1滑车组的动滑车改变为双门滑车，即将1－1滑车组改变为2－1滑车组，则施力方向变为与负载重量同方向，或者任意其它方向。如左图所示，从动滑车引出的绳索段数目为 3 {\displaystyle 3} ，所以输入力为 W / 3 {\displaystyle W/3} ，机械利益为 3 {\displaystyle 3} 。

带和带轮系统

平型带安装于具有平滑的轮面的带轮外围。

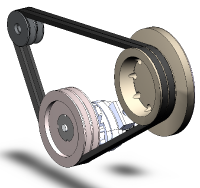
一对V型带和带轮系统

带和带轮系统的特征是两个或多个滑轮被紧套于同一个传动带。这设置允许机械功率、力矩、速度从一个旋转轴传递至另一个旋转轴。假若滑轮的直径不同，则可以借此过程，获得机械利益。

带传动与 链传动 类似，带轮的表面是平滑的，机械利益大约是两个带轮之间的直径比例，而不是对于 链轮 或齿轮精确计算获得的齿轮速比。

参阅

差动滑车 （ 英语 ： Differential pulley ）

阿特伍德机

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。