洛希瓣的定义

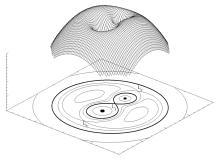
在质量比为2的联星中，在相同转动方向系统下的三度空间洛希等位面。在等位面下面底部的泪滴形图被称为恒星的洛希瓣。L1, L2 and L3是引力互相抵消的拉格朗日点。如果恒星的物质已经充满了洛希瓣，则物质可以从恒星L1点的鞍部流向它的伴星Source。

在有着圆轨道的联星系统中，它通常能在随着天体一起转动的坐标系统中很有效的描述。除了引力之外还必须考虑离心惯性力。可以用势能一起描述这两种力，因此，例如，恒星的表面可以沿着等位面表面伸展。

在靠近个别的恒星时，相同的引力等位面形状是接近球形的，并且与靠近的恒星是同心球。在离恒星系统较远处，等位面的形状接近椭球体，并且延伸的方向平行于两颗恒星的联心轴线的方向。临界的等位面和系统本身的L1拉格朗日点相交会，在各自瓣图中形成在两颗恒星之间的8字形瓣图。这个临界的等位面定义出洛希瓣。

当相对于共同转动系统中的物质流动时，似乎会采取像科氏力的行为。这不是从洛希瓣的模型推导倒出来的，科氏力是不守恒力（也就是说，不能以标量来处理）。

质量转移

当一颗恒星"超越了洛希瓣"，它的表面扩展至洛希瓣之外，同时超越过洛希瓣的物质会经由L1拉格朗日点掉落至伴星的落希瓣之内。在联星演化的过程中，这种质量传输被称为洛希瓣溢流（洛希瓣超流）。

原则上，质量传输可能导致天体完全的解体，因为质量的减少会导致落希瓣的萎缩。但是，有几个原因使这种情况通常不至于发生。首先，捐助恒星的质量减缩会导致捐助者的缩小，这可能会阻碍后续的捐助。其次，在联星的两颗恒星之间的质量传输还包括了角动量的传输。当物质从质量较大的恒星捐助给原本质量较小的恒星增生时，通常会导致轨道的收缩，反过来造成联星轨道的膨胀（根据质量守恒和角动量守恒的设想）。联星轨道的扩大将导致较少的戏剧性收缩，或甚至会扩大捐助者的洛希瓣，而这通常会阻止捐助者受到破坏。

要测量质量传输的稳定性和捐助者确实的萎缩，需要实际计算捐助恒星的半径和之后的洛希瓣质量传输；如果恒星扩张的比洛希瓣的缩小还快，或是缩小的比洛希瓣拖拉的时间还慢，质量的传输会变得不稳定而导致捐助恒星可能的瓦解。如果捐助恒星扩张的较慢，或是收缩得比洛希瓣快，质量的传输通常会保持稳定并且可以持续很长的时间。

由于洛希瓣溢流的质量传输几种易懂的天文现象之一，包括大陵五系统，再发新星（包含一颗红巨星和一颗白矮星的联星，并且相距的距离组以使红巨星的物质逐渐流动至白矮星）、X射线联星和毫秒脉冲星。

洛希瓣的几何

洛希瓣的精确形状取决于质量比，并且必须经过数值的计算。但是，在多数的用途中，都使用形状近似和有着相同体积的洛希瓣。一个有着球形和半径的近似计算公式如下：

r1A=0.38+0.2log⁡ ⁡ -->M1M2{\displaystyle {\frac {r_{1}}{A}}=0.38+0.2\log {\frac {M_{1}}{M_{2}}}} for 0.3<M1M2<20{\displaystyle 0.3

并且

r1A=0.46224(M1M1+M2)1/3{\displaystyle {\frac {r_{1}}{A}}=0.46224\left({\frac {M_{1}}{M_{1}+M_{2}}}\right)^{1/3}} 对于 M1M2<0.8{\displaystyle {\frac {M_{1}}{M_{2}}}<0.8}

此处，A是系统的半长轴，r1{\displaystyle r_{1}}是环绕着质量为M1{\displaystyle M_{1}}的洛希瓣的半径。这些公式大约可以精确到2%以内。

相关条目

联星

希尔球

洛希极限

Rocheworld for a hard science fiction novel based on this concept.

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。