基本几何性质

正一百二十胞体的顶点图是正四面体，棱图是正三角形，若其棱长为a，则其超体积为 15 ( 105 + 47 5 ) a 4 4 {\displaystyle {\cfrac {15(105+47{\sqrt {5}})a^{4}}{4}}} ，表体积是(450+210√5)a 。其二胞角是144°，这意味着它不能独自完成四维欧几里得空间的堆砌，但戴维斯首先描述了四维双曲空间的一种正一百二十胞体堆砌，这种存在于紧凑双曲流形的堆砌有施莱夫利符号{5,3,3,5}。

若一个正一百二十胞体的棱长为1，则其外接超球的半径为 10 + 3 2 2 ≈ ≈ --> 3.702459174 {\displaystyle {\begin{smallmatrix}{\frac {{\sqrt {10}}+3{\sqrt {2}}}{2}}\approx 3.702459174\end{smallmatrix}}} ,其外中交超球（经过正一百二十胞体每条棱的中点的三维超球）半径为 15 + 2 3 2 ≈ ≈ --> 3.668542481 {\displaystyle {\begin{smallmatrix}{\frac {{\sqrt {15}}+2{\sqrt {3}}}{2}}\approx 3.668542481\end{smallmatrix}}} ，其内中交超球（经过正一百二十胞体每个面的中心）半径为 10 ( 29 5 + 65 ) 10 ≈ ≈ --> 3.603414649 {\displaystyle {\begin{smallmatrix}{\frac {\sqrt {10(29{\sqrt {5}}+65)}}{10}}\approx 3.603414649\end{smallmatrix}}} ,其内切超球半径为 3 5 + 7 4 ≈ ≈ --> 3.427050983 {\displaystyle {\begin{smallmatrix}{\frac {3{\sqrt {5}}+7}{4}}\approx 3.427050983\end{smallmatrix}}} 。

顶点坐标

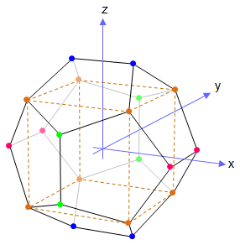
如果以其中心为原点，正一百二十胞体600个顶点坐标是以下的全排列： (0, 0, ±2, ±2) (±1, ±1, ±1, ±√5) (±φ-2, ±φ, ±φ, ±φ) (±φ-1, ±φ-1, ±φ-1, ±φ2) 及以下的全偶排列： (0, ±φ-2, ±1, ±φ2) (0, ±φ-1, ±φ, ±√5) (±φ-1, ±1, ±φ, ±2) （φ是黄金分割，(1+√5)/2）

对称群构造

正一百二十胞体与正六百胞体一样具有H 4 对称群构造，对应施莱夫利符号{5,3,3}，Coxeter-Dynkin符号 。拥有H n 对称群的凸正多胞形属于正五边形形家族，这个家族在五维及以后就只有双曲堆砌成员。

特殊结构

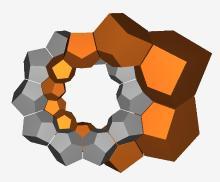
两个互相“交织”（实是相邻，交织是四维超球曲率导致的结果）的“大圆”

大圆结构

对于正一百二十胞体来说，其与其三维类比正十二面体的不同之处之一就是构成正一百二十面体的表面——正十二面体的对面是平行的，这意味着如果把正一百二十胞体当作超球面堆砌的话，会有10个胞以平行的对面首尾相接，构成大圆（这种大圆在不同方向上有12个）。（从这点中可以不用解析几何求导就可以求出二胞角，它等于正十边形的内角144°）。

分层结构

同时，我们也可以把其中一个上文所述的这种大圆当作“赤道”，以“纬度”把正一百二十胞体的胞分成9层，每层分别有1（北极）、12（北极圈）、20、12（北回归线） 、30（赤道）、12（南回归线）、20、12（南极圈）、1（南极）个胞，每两层的仰角相差36°。

其它参考

哈罗德·斯科特·麦克唐纳·考克斯特, Regular Polytopes , 第三版, Dover Publications, 1973. ISBN 0-486-61480-8.

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。