参见采样采样定理信号连续信号离散时间信号

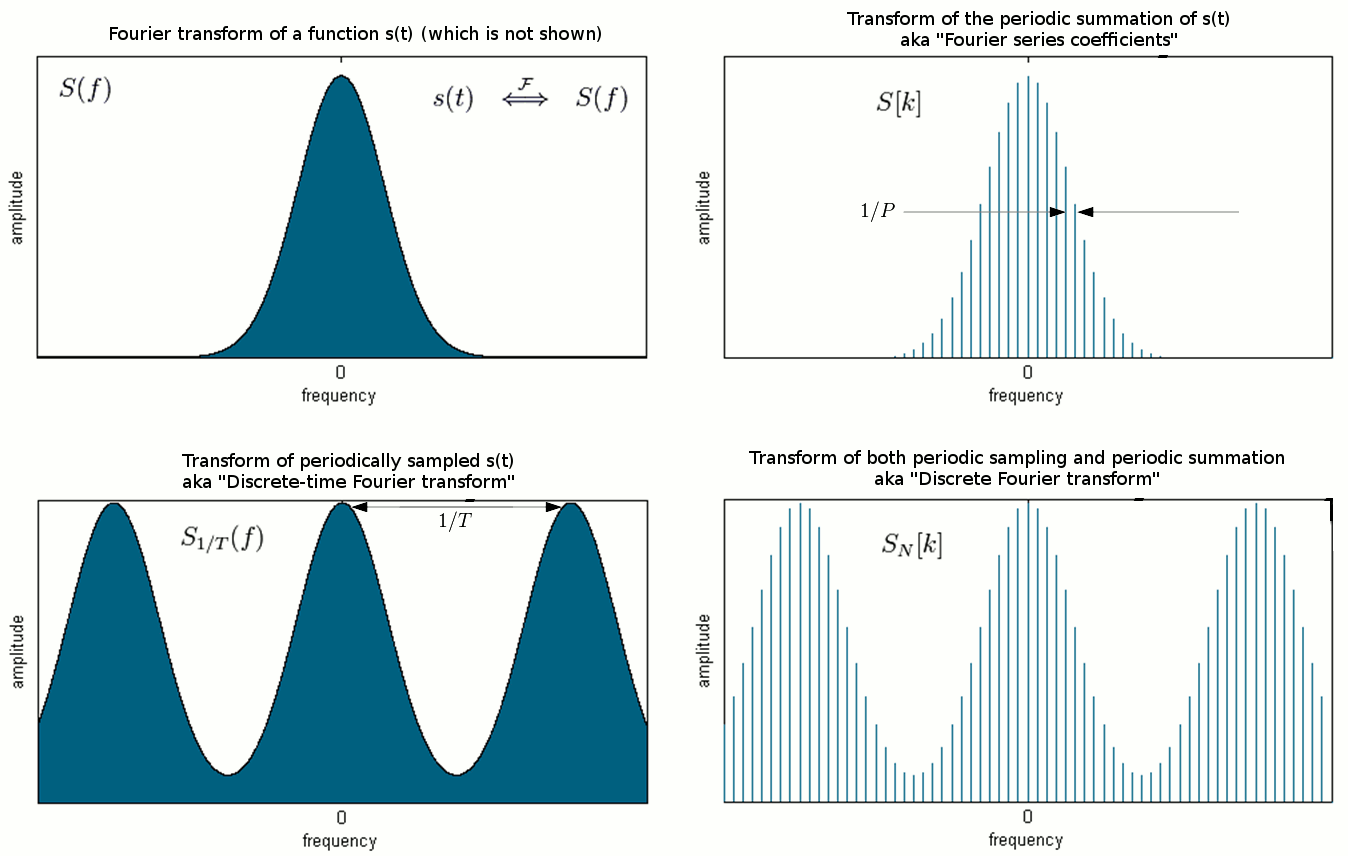
定义一组离散的实数或复数：x[n]（n为所有整数）的离散时间傅里叶变换是产生以频率为变量的周期函数的一个傅里叶级数。当频率变量ω的单位是归一化的弧度/样本时，周期为2π，而傅里叶级数为：此频率域函数的性质源于泊松求和公式（英语：Poissonsummationformula）。令X(f)为任意函数x(t)的傅里叶变换，采样间隔为T（秒），等价于序列x[n]（或与之成正比），即T⋅⋅-->x(nT)=x[n]{\displaystyleT\cdotx(nT)=x[n]}。则以傅里叶级数表示的周期函数是X(f)的周期求和。赫兹以赫兹（周期/秒）为单位的频率f{\displaystyle\textstylef}的话就会是：图一.傅立叶变换（左上）和左下的其周期求和（DTFT）的图示。右下角显示了用离散傅里叶变换（DFT）计算DTFT的采样。整数k的单位为转/样本，采样频率是1/T，fs（样本/秒...

形成阋神星，已知最大的黄道离散天体，和它的卫星阋卫一（迪丝诺美亚，中央偏左的小光点）。我们对离散盘的所知非常有限，虽然天文学的主流观点认为它是太阳系形成的早期过程中，因为海王星向外迁徙造成的引力扰动才被从柯伊伯带散射入高倾斜和高离心率的轨道内。相比之下，柯伊伯带像是一个相对“圆”和“平坦”的甜甜圈，以平和的圆轨道（QB1天体）和略为椭圆的共振轨道（类冥天体），将天体约束在30至44天文单位的圆环内；离散盘内的黄道离散天体轨道环境就比较怪异了。黄道离散天体，就以矮行星阋神星为例，在垂直黄道方向上的距离几乎和平行方向上与太阳的距离一样远；轨道模拟也显示黄道离散天体的轨道是怪异且不稳定的，并且最终会从太阳的核心区域抛至奥尔特云甚至更遥远的地方。有些迹象显示半人马群只是单纯的从柯伊伯带被向内抛射，而不是向外抛射的天体，可以称为“内海王星天体”（cis-Neptunianobject）。事实上，有些...

性质因为拓扑群是齐次的，你只需要查看一个单一的点就能确定这个群是否为离散的。特别是，拓扑群是离散的，当且仅当包含单位元的单元素集合是开集。离散群是和零维李群同样的东西(不可数离散群不是第二可数的，所以要求李群满足这个公理的作者不把这些群认做李群)。离散群的单位元单元就是平凡子群而单元的群同构于这个群自身。因为只有在有限集合上的豪斯多夫拓扑是离散拓扑，有限豪斯多夫拓扑群必然是离散群。可得出所有的豪斯多夫群的有限子群是离散群。G的离散子群H是馀紧致(cocompact)的，如果有G的紧子集K使得HK=G。离散正规子群在覆盖群和局部同构群的理论中扮演重要角色。连通群G的离散正规子群必然位于G的中心并因此是阿贝尔群。其他性质:所有离散群的子群都是离散群。所有离散群的商群都是离散群。有限个离散群的乘积是离散群。离散群是紧群当且仅当它是有限的。所有离散群都是局部紧群。所有豪斯多夫群的离散子群都是闭合的...

定义在信息论中，信号是一种信息流。我们感兴趣的大部分信号都可表述为时间或位置的函数。任何携带信息的物理量皆可以作为信号。信号本身所携带的信息是我们的目的，从中提取有需要有用的信号，抑制干扰部分是信号处理的目标。连续与离散按照信号时间向量的不同，可以分为：连续时间信号（Continuous-Time）和离散时间信号（Discrete-Time）。连续信号是时间的连续函数，而离散信号是时间的离散函数。模拟与数字所有维度上均连续的信号是模拟信号，所有维度上均离散的信号则是数字信号。数字信号是通过对模拟信号时间、幅度维度上离散化产生的。一些信号的例子运动声音影像画面频率分析见频域。无论对于连续信号还是离散信号，分析信号的频谱都是一种非常有效的方法。例如一个信号通过线性时不变系统，则系统输出频谱即为信号频谱与系统频率响应之积。熵信号的另一重要特性便是熵。相关主题噪声信噪比讯号处理影像处理