与正十二面体的关系

在平面上，正多边形内接到圆时，边数越多，占圆面积的百分比就越高；而在三维空间中，这个规则却不可推广——当正十二面体和正二十面体内接到一个球时，前者约占66.4909%，后者仅占60.5461%。

体积与表面积

若有一个边长为 a 的正二十面体，则它的外接球（同时过该正二十面体所有顶点的球）的半径为：

则有内切球（同时和该正二十面体所有面相切的球）的半径为：

另外，若有一个球同时过该正二十面体所有边的中点，那它的半径为：

其中 φ （也称作 τ ）为黄金比例。

体积与表面积

若用 A 表示表面积、 V 表示体积，而 a 是正二十面体的边长，则有：

后者 F=20 约为正四面体的20倍，因为20面体以外接球球新为中心可以切割出20个四面体，其中的四面体的体积是底面积的三分之一倍， r i 是高的 √3a /4 倍。

的外接球体的体积填充率是：

直角坐标系

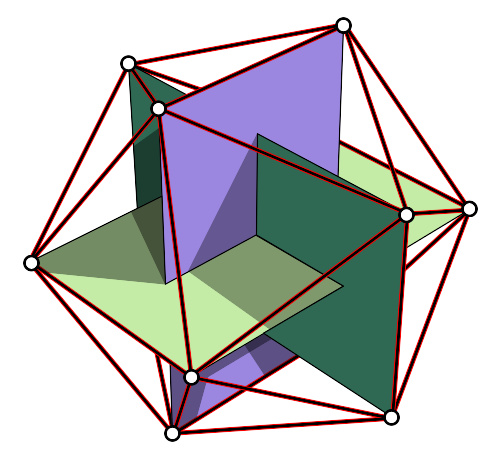
正二十面体的顶点能共同分成五组，每组拥有三个同心、相互垂直的黄金矩形。

在直角坐标系中，一个边长为二、重心在圆点的正二十面体的坐标分别为：

其中 φ = 1 + √ 5 / 2 是黄金比例（或记为 τ ）。值得注意的是，这些顶点能共同形成五组，每组拥有三个同心、相互垂直的黄金矩形，其边形成 博罗梅安环 （ 英语 ： Borromean rings ） ，其中，前者是因为正二十面体与黄金比例有密切的关系。 如果原始的二十面体的边长为1，那么它的对偶——正十二面体的边长就是 √ 5 − 1 / 2 ，正好是一个黄金比例。

一个由塑胶棒和磁铁与金属球连接的正二十面体模型

12条边的一个正八面体可以被细分在黄金比例，使所得到的顶点可构成一个正二十面体。这首先要使沿着八面体边的向量连成一个有界的环，再沿着向量的方向以黄金比例作分割。

球面坐标

正二十面体是一个D 5d 二面体对称对称的一个双五角锥反角柱，且顶点可以定义在球面坐标系上，其中两个顶点在球的两极，其余在纬度±arctan(1/2)的位置。可以发现剩余的10顶点属于反棱柱对称，从一个定点，经度每36°做一次极轴与赤道镜射，直到回到原始点。

与黄金分割的关系

若以正二十面体的中心为原点，各顶点的坐标分别为 {(0,±1,±Φ), (±1,±Φ,0), (±Φ,0,±1) }，在此 Φ = √ 5 − 1 / 2 ，即黄金分割数。因此，这些顶点能共同形成五组，每组拥有三个同心、相互垂直的黄金矩形。

正交投影

正二十面体有3种特殊的正交投影，分别正对着一个面、一条棱、一个顶点。

其它事实

正二十面体有43,380种不同的展开图。

若要将正二十面体的表面涂色而相邻的面的颜色不同，则至少需要3种颜色。

内接与同一球的正二十面体和正十二面体，正二十面体所占球的体积（60.54%）要小于正十二面体所占的体积（66.49%）。

通过一系列等夹角线段构造正二十面体

以下构建正二十面体的方法避免了使用更基础的方法时必要的在数域 Q [ 5 ] {\displaystyle \mathbb {Q} [{\sqrt {5}}]} 中的复杂计算。 正二十面体的存在性依赖于 R 3 {\displaystyle \mathbb {R} ^{3}} 中6条等夹角线的存在性。事实上，我们很容易便可以发现，这样一组等夹角线与欧几里得空间中的球心在等夹角线所共的交点的球相交，得出的交点即是一个正二十面体的12个顶点。从相反方向考虑，假设这里存在一个正二十面体，它的6对相对顶点的连线（对角线）就形成了那样一个等夹角线系统。 为了构建这样一个等夹角线系统，我们开始于一个6×6方形矩阵。

通过直接的计算，我们可以得出 A =5 I （在这里 I 是6×6单位矩阵）。这表明矩阵 I 的特征值是√5和-√5，并且它们的复杂性都是3，因为 A 是对称的，并且它的迹是0。 矩阵 A + 5 I {\displaystyle \scriptstyle A+{\sqrt {5}}I} 在商空间 R 6 / ker ⁡ ⁡ --> ( A + 5 I ) {\displaystyle \mathbb {R} ^{6}/\ker(A+{\sqrt {5}}I)} 中引出同构个同构于 R 3 {\displaystyle \mathbb {R} ^{3}} 的欧几里得结构因为它的核 ker ⁡ ⁡ --> ( A + 5 I ) {\displaystyle \ker(A+{\sqrt {5}}I)} 是三维的。在 R 6 {\displaystyle \mathbb {R} ^{6}} 中，它的六条坐标轴线 R v 1 , … … --> , R v 6 {\displaystyle \mathbb {R} v_{1},\dots ,\mathbb {R} v_{6}} 在投影 π π --> : R 6 ⟶ ⟶ --> R 6 / ker ⁡ ⁡ --> ( A + 5 I ) {\displaystyle \pi :\mathbb {R} ^{6}\longrightarrow \mathbb {R} ^{6}/\ker(A+{\sqrt {5}}I)} 下的图像形成了这样一个在 R 3 {\displaystyle \mathbb {R} ^{3}} 中由六条等夹角线组成的系统，它们都相交于一点，两两之间都夹着锐角 arccos 1 5 {\displaystyle \scriptstyle {\arccos }{\tfrac {1}{\sqrt {5}}}} 。± v 1 ，...，± v 6 向 A 的√5-特征空间的正交投影形成了正二十面体的12个顶点。 正二十面体另一个直接的构造用到了交错群 A 5 的群表示论方法，它直接利用了正二十面体的等距同构。

半正涂色和子对称群

正二十面体作为扭棱四面体，可以通过旋转正四面体的正三角形面，并在4个顶点处插入新的三角形，在原来的6条棱处插入新的一对三角形来构造

作为正多面体之一，正二十面体拥有较高的对称性，它的所有面在几何上都是相同的，不可区分的。可是我们也可以想象将正二十面体的面“涂上”不同的“颜色”，使它其的不同面拥有不同的“几何意义”，使其拥有不同的次级对称性。正二十面体有三种不同的半正涂色方法，可以按照一个顶点引出的5个面的涂色来标记为11213、11212、11111。正二十面体可以被描述为 扭棱 （ 英语 ： Snub (Geometry) ） 正四面体，具有手征性 正四面体对称性 （ 英语 ： tetrahedral symmetry ） ；它亦可以被描述成交错截顶正八面体，有 五角十二面体对称性 （ 英语 ： pyritohedral symmetry ） 。这个具有五角十二面体对称的正二十面体也被叫做伪二十面体是五角十二面体的对偶。

与其它几何图形的关系

正二十面体是正二十面体家族的一员：

作为扭棱正四面体和交错截顶正八面体，正二十面体也是正四面体家族和正八面体家族的一员：

正二十面体在拓扑上与其它一系列的正三角形镶嵌{3,n}和一系列的五阶正镶嵌{n,5}相关联：

正二十面体和三个星形正多面体有着相同的顶点排布。其中与大十二面体还有相同的棱排布：

虽然由于正二十面体的二面角太大（约138.189685°>120°），因此正二十面体不可能密铺三维欧几里得空间，但它可以密铺适当的双曲空间，称为 三阶正二十面体堆砌 （ 英语 ： Icosahedral honeycomb ） ，每条棱处有三个正二十面体相交，每个顶点处有12个正二十面体相交，应此顶点图是正十二面体，施莱夫利符号{3,5,3}，是四个三维双曲空间中的正堆砌之一。

应用

二十面的骰子

电子显微镜下观察的金原子

γ-硼的结构

由于正二十面体非常均匀，且有20个面，因此适合作成骰子。

在生物学中

某些病毒，如疱疹病毒科、诺罗病毒，拥有正二十面体的衣壳。 在有些细菌中还发现一些具有二十面体形状的各种细菌的胞器， 还有二十面体的壳包住的酶使不稳定的活化复合体得以建构BMC等不同类型的蛋白质。

1904年，恩斯特·海克尔发表了一些放射虫的种类，包括Circogonia二十面体（ Circogonia icosahedra ），其骨架的形状像一个正二十面体。

参考文献

Klein, Felix,Lectures on the ikosahedron and the solution of equations of the fifth degree, 1888, Dover edition ISBN 978-0-486-49528-6.

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。