概述

贝尔不等式为： |Pxz-Pzy|≤1+Pxy 。

其中，Ax为正的意思为在x轴上观察到A量子的自旋态为正，而Pxz代表Ax为正和Bz为正的相关性。

在经典力学中，此不等式成立。在量子世界中，此不等式却不成立。

贝尔定理意味着，阿尔伯特·爱因斯坦所主张的定域性原理，其预测不符合量子力学理论。由于很多实验的结果与量子力学理论的预测一致，显示出的 量子关联 （ 英语 ： quantum correlation ） 远强过定域隐变数理论所能够解释，所以，物理学者拒绝接受定域实在论对于这些实验结果的解释。陷入找不到满意解答的窘境，物理学者只能无可奈何地勉强承认这是一种非因果关系的 超光速效应 （ 英语 ： superluminal effect ） 。

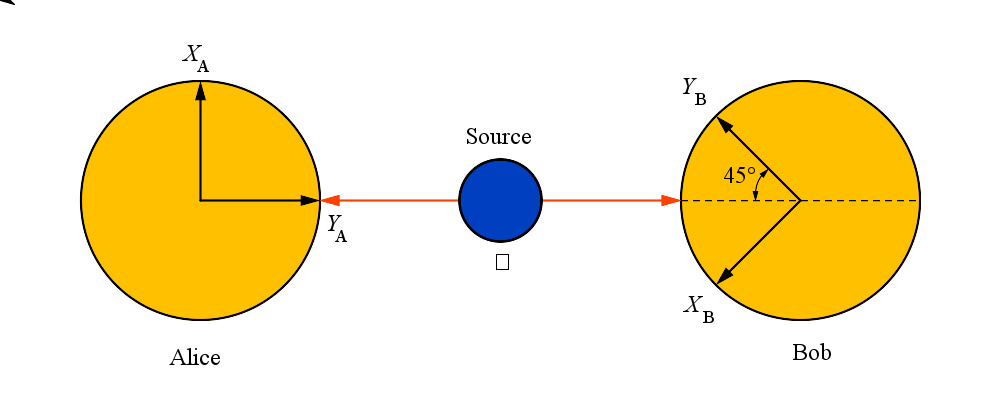
  对于像光子一类的粒子，贝尔定理的实验验证示意图。不稳定粒子的衰变会生成单态粒子对，其两颗粒子会分别朝着相反方向移动。假设，在与衰变地点相隔一段距离的两个地点，分别以各种不同夹角角度 θ θ --> {\displaystyle \theta } 任意设定为实验参数，然后测量这两颗粒子的自旋，则得到的数据可以计算出这系统的纠缠性质。

贝尔定理可以应用于任何由两个相互纠缠的量子位元所组成的量子系统。最常见的范例是纠缠于自旋或偏振的粒子系统。

继续发展爱因斯坦-波多尔斯基-罗森佯谬（简称EPR佯谬）的论述 （但是选择采用自旋的例子，如同戴维·玻姆版本关于EPR吊诡的论述 ），贝尔精心设计出一个思想实验：从衰变生成的两颗处于单态的自旋1/2粒子会分别朝着相反方向移动，在与衰变地点相隔遥远的两个地点，分别沿着独立选择的直轴测量两个粒子的自旋，每一次测量得到的结果是“向上自旋”（标记为“+”）或“向下自旋”（标记为“−”）。

在两个地点测量得到一致结果的概率，会因为两根直轴 a {\displaystyle \mathbf {a} } 与 b {\displaystyle \mathbf {b} } 之间的夹角角度 θ θ --> {\displaystyle \theta } 而变化，除了平行或反平行的设置（ θ θ --> {\displaystyle \theta } 为0°或180°），会遭受到不确定性。所以，贝尔定理只能应用于从多次测量得到的统计结果。现在设定实验规则，假设爱丽丝与鲍伯分别独自在这两个地点测量，若在某一次测量，爱丽丝测量的结果为向上自旋，而鲍伯测量的结果为向下自旋，则称这两个结果一致，相关系数为"+1"，反之亦然；否则，就像如下，若爱丽丝与鲍伯测量的结果都为向上自旋或都为向下自旋，则两个结果不一致，相关系数为"-1"。那么，假设 a {\displaystyle \mathbf {a} } 与 b {\displaystyle \mathbf {b} } 相互平行，则测量这些量子纠缠粒子永远会得到一致的结果（完全相关）；假设两根直轴相互垂直，则只有50%概率会得到一致的结果，得到不一致结果的概率也是50%。以下列出这些基本案例：

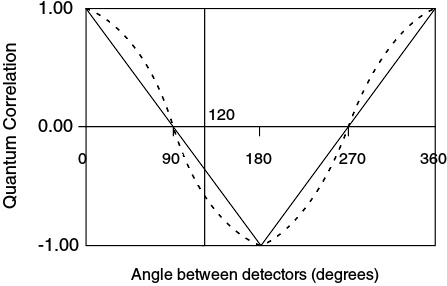
  对于自旋的量子相关性（假定100%侦测效率），局域隐变数理论的预测以实线显示，量子力学预测以虚线显示。

如右图所示，假设两根直轴的夹角角度 θ θ --> {\displaystyle \theta } 在上述基本案例角度之间，则局域隐变数理论的成立意味着量子相关性呈线性变化。但是根据量子力学理论，量子相关性应呈角度的余弦 cos ⁡ ⁡ --> θ θ --> {\displaystyle \cos \theta } 变化。重要关键是，实际纠缠实验结果支持量子力学理论的预测。

贝尔推导出定域实在论会产生的结果。在这导引内，除了要求基本的一致化以外，不做任何其它特别的假定，贝尔发现的数学问题，很明显地不同于量子力学的预测，更不同于稍后得到的实验观测结果。这样，贝尔定理排除了定域隐变数为量子力学的可信解释，虽然非定域隐变数理论的大门仍旧敞开无碍。贝尔结论 ：

这些年来，有许多实验企图验证贝尔定理，并得出贝尔不等式被违背的实验数据。但很多关于这些实验的不足之处都已被找到，包括“侦测漏洞”、“通讯漏洞”等等 。由于科技的进步，实验也逐步的改良，更能够针对这些漏洞给予补足，但是至今 (2014) 没有任何实验能够完全地补足这些漏洞 。不过物理学家相信，完美的贝尔定理实验可以在5年内出现。虽然完美的实验尚未出现，但主流量子力学教科书已将贝尔定理视为基础物理定理 。但是，没有任何物理定理能够毫无疑问的被接受；仍有些物理学者反驳，贝尔定理隐藏的假定或实验漏洞否定了理论的正确性 。

参阅

贝尔实验的预测（ Quantum mechanical Bell test prediction ）

CHSH不等式（ CHSH inequality ）

GHZ实验（ GHZ experiment ）

莱格特不等式（ Leggett inequality ）

莱格特-皋格不等式（ Leggett-Garg inequality ）

莫特问题（ Mott problem ）

任宁格负结果实验（ Renninger negative-result experiment ）

参考文献

A. Aspect et al., Experimental Tests of Realistic Local Theories via Bell"s Theorem , Phys. Rev. Lett. 47 , 460 (1981)

A. Aspect et al., Experimental Realization of Einstein-Podolsky-Rosen-Bohm Gedankenexperiment: A New Violation of Bell"s Inequalities , Phys. Rev. Lett. 49 , 91 (1982).

A. Aspect et al., Experimental Test of Bell"s Inequalities Using Time-Varying Analyzers , Phys. Rev. Lett. 49 , 1804 (1982).

A. Aspect and P. Grangier, About resonant scattering and other hypothetical effects in the Orsay atomic-cascade experiment tests of Bell inequalities: a discussion and some new experimental data , Lettere al Nuovo Cimento 43 , 345 (1985)

B. D"Espagnat,The Quantum Theory and Reality, Scientific American, 241 , 158 (1979)

J. S. Bell, On the problem of hidden variables in quantum mechanics , Rev. Mod. Phys. 38 , 447 (1966)

J. S. Bell, On the Einstein Podolsky Rosen Paradox , Physics 1 , 3, 195-200 (1964)

J. S. Bell, Introduction to the hidden variable question , Proceedings of the International School of Physics "Enrico Fermi", Course IL, Foundations of Quantum Mechanics (1971) 171–81

J. S. Bell, Bertlmann’s socks and the nature of reality , Journal de Physique, Colloque C2, suppl. au numero 3, Tome 42 (1981) pp C2 41–61

J. S. Bell, Speakable and Unspeakable in Quantum Mechanics (Cambridge University Press 1987) [A collection of Bell"s papers, including all of the above.]

J. F. Clauser and A. Shimony, Bell"s theorem: experimental tests and implications , Reports on Progress in Physics 41 , 1881 (1978)

J. F. Clauser and M. A. Horne, Phys. Rev D 10 , 526–535 (1974)

E. S. Fry, T. Walther and S. Li, Proposal for a loophole-free test of the Bell inequalities , Phys. Rev. A 52 , 4381 (1995)

E. S. Fry, and T. Walther, Atom based tests of the Bell Inequalities — the legacy of John Bell continues , pp 103–117 of Quantum [Un]speakables , R.A. Bertlmann and A. Zeilinger (eds.) (Springer, Berlin-Heidelberg-New York, 2002)

R. B. Griffiths, Consistent Quantum Theory" , Cambridge University Press (2002).

L. Hardy, Nonlocality for 2 particles without inequalities for almost all entangled states . Physical Review Letters 71 (11) 1665–1668 (1993)

M. A. Nielsen and I. L. Chuang, Quantum Computation and Quantum Information , Cambridge University Press (2000)

P. Pearle, Hidden-Variable Example Based upon Data Rejection , Physical Review D 2 , 1418–25 (1970)

A. Peres, Quantum Theory: Concepts and Methods , Kluwer, Dordrecht, 1993.

P. Pluch, Theory of Quantum Probability , PhD Thesis, University of Klagenfurt, 2006.

B. C. van Frassen, Quantum Mechanics , Clarendon Press, 1991.

M.A. Rowe, D. Kielpinski, V. Meyer, C.A. Sackett, W.M. Itano, C. Monroe, and D.J. Wineland, Experimental violation of Bell"s inequalities with efficient detection ,(Nature, 409, 791–794, 2001).

S. Sulcs, The Nature of Light and Twentieth Century Experimental Physics , Foundations of Science 8 , 365–391 (2003)

S. Gröblacher et al., An experimental test of non-local realism ,(Nature, 446, 871–875, 2007).

D. N. Matsukevich, P. Maunz, D. L. Moehring, S. Olmschenk, and C. Monroe, Bell Inequality Violation with Two Remote Atomic Qubits , Phys. Rev. Lett. 100, 150404 (2008).

进阶阅读

以下列出一些专门为一般读者所撰写、涉及贝尔定理的著作：

Amir D. Aczel, Entanglement: The greatest mystery in physics (Four Walls Eight Windows, New York, 2001).

A. Afriat and F. Selleri, The Einstein, Podolsky and Rosen Paradox (Plenum Press, New York and London, 1999)

J. Baggott, The Meaning of Quantum Theory (Oxford University Press, 1992)

N. David Mermin, "Is the moon there when nobody looks? Reality and the quantum theory", in Physics Today , April 1985, pp. 38–47.

Louisa Gilder, The Age of Entanglement: When Quantum Physics Was Reborn (New York: Alfred A. Knopf, 2008)

Nick Herbert, Quantum Reality: Beyond the New Physics (Anchor, 1987, ISBN 0-385-23569-0)

D. Wick, The infamous boundary: seven decades of controversy in quantum physics (Birkhauser, Boston 1995)

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。