定义

令 I 为（可能无穷的）指标集，并设 X i 对于 I 中由 i 所对应的每一个拓扑空间。置 X = Π X i ，也即集合 X i 的卡积。对于每个 I 中的 i ，我们有一个 标准投影 p i : X → X i 。 X 上的 积拓扑 定义为所有投影 p i 在该拓扑下连续的最疏拓扑（也就是开集最少的拓扑）。该乘积拓扑有时也称为 吉洪诺夫拓扑 。

很明显， X 上的乘积拓扑可以表述为形为 p i ( U )的集合生成的拓扑，其中 i 属于 I ，而 U 是 X i 的一个开集。换句话说，集合{ p i ( U )}构成 X 上的拓扑的子基。 X 的子集是开的当且仅当它是(可能无穷多的)的有限个形为 p i ( U )的集合的交集的并集。 p i ( U )有时称为开柱，而它们的交集称为柱集。

我们可以用构成 X 的空间 X i 的基来表述乘积拓扑的基。设对于每个 i 属于 I ，选取一个集合 Y i 或者是整空间 X i 或者是该空间的一个基，并且满足 X i = Y i 对于除了有限个 I 中的 i 之外的所有 i 成立。令 B 为集合 Y i 的卡积。所有可以这样构造的 B 集合的族构成乘积空间的一个基。这意味着有限多空间的乘积有一个由 X i 的基元素的乘积组成的基。

如果指标集为有限（特别是，对于两个拓扑空间的乘积），则积拓扑有更简单的表述。这个情况下，每个 X i 的拓扑的乘积构成 X 上的拓扑的一个基。一般来讲， X i 的拓扑的乘积构成一个称为 X 上的盒拓扑的基。一般情况下，盒拓扑比积拓扑更细，但是对于有限乘积，它们是相同的。

例子

从实直线 R 上的标准拓扑开始，定义 n 份 R 的乘积，就得到普通的 R 上的欧几里得拓扑。

康托尔集同胚于可数个离散空间{0,1}的乘积而无理数的空间同胚于可数个自然数集的乘积，每个集合也是采用离散拓扑。

属性

乘积空间 X 加上标准投影，可以用如下的泛性质来刻划：若 Y 是拓扑空间，并且对于每个 I 中的 i ， f i : Y → X i 是一个连续映射，则存在 恰好一个 连续映射 f : Y → X 满足对于每个 I 中的 i 如下交换图成立：

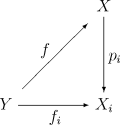
这表明乘积空间是拓扑空间范畴中的积。从上述泛性质可以得出映射 f : Y → X 连续当且仅当 f i = p i o f 对于所有 I 中的 i 连续。在很多情况下，检查分量函数 f i 的连续性更为方便。检验映射 f : Y → X 是否连续通常更难；可以试着用某种方式利用 p i 连续这一点。

除了连续，标准投影 p i : X → X i 也是开映射。这表示每个积空间的开子集投影到 X i 上还是开集。反过来不真：若 W 是到所有 X i 的投影都是开集的积空间的子空间，则 W 不一定是 X 中的开集。（例如， W = R \ (0,1) .）标准投影通常不是闭映射。

积拓扑有时称为 点式收敛拓扑 ，因为： X 上的一个序列（或者网）收敛当且仅当它所有到 X i 的投影收敛。特别是，如果考虑所有在空间 X = R 对于所有 I 上的实值函数，在积拓扑上的收敛就是函数的点式收敛。

积拓扑的一个重要定理就是吉洪诺夫定理：任何紧致空间的乘积是紧致的。对于有限乘积很容易证明，而其一般情况等价于选择公理。

和其它拓扑概念的联系

可分离性

紧致性

连通性

每个"局部看起来"一个标准投影 F × U → U 的空间称为纤维丛。

参看

盒拓扑

不交并 (拓扑学)

商空间

子空间拓扑

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。