平移

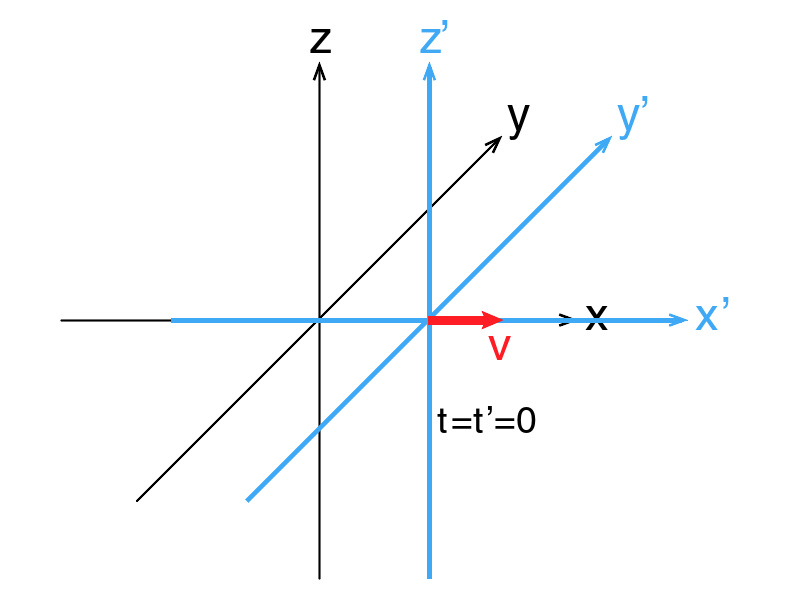
伽利略变换示意图

伽利略变换建基于人们加减物体速度的直觉。在其核心，伽利略变换假设时间和空间是绝对的。

这项假设在洛伦兹变换中被舍弃，因此就算在相对论性速度下，洛伦兹变换也是成立的；而伽利略变换则是洛伦兹变换的低速近似值。

以下为伽利略变换的数学表达式，其中 ( x , y , z , t ) 和 ( x ′, y ′, z ′, t ′) 分别为同一个事件在两个坐标系S和S"中的坐标。两个坐标系以相对均速运行（速度为 v ），运行方向为 x 和 x ′ ，原点在时间为t=t"=0时重合。

最后一条方程式意味着时间是不受观测者的相对运动影响的。

利用线性代数的术语来说，这种变换是个错切，是矩阵对向量进行变换的一个过程。当参考系只沿着 x 轴移动时，伽利略变换只作用于两个分量：

虽然在伽利略变换中没有必要用到矩阵表达法，但是用了矩阵就可以和狭义相对论中的变换法进行比较。

三种伽利略变换

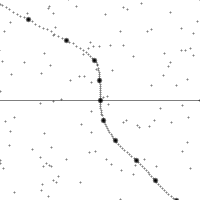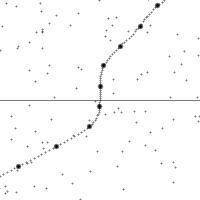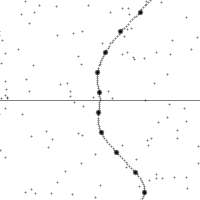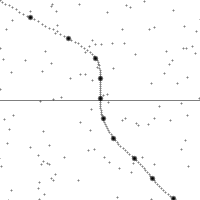
沿着一个加速中观测者的世界线所看到的时空。 纵轴为时间，横轴为距离，虚线为观测者在时空中的轨迹。图的下半部是已经发生了的事件，上半部则是未来的事件。图中小点为时空中的事件。 世界线的斜率为观测者的相对速率。注意观测者在加速时所看到的时空会进行错切。

伽利略变换可以唯一写成由时空的旋转、平移和匀速运动复合而成的函数。 设 x 为三维空间中的一点， t 为一维时间中的一点。时空当中的任何一点可以表达为有序对( x , t )。速度为 v 的匀速运动表达为 ( x , t ) ↦ ↦ --> ( x + t v , t ) {\displaystyle ({\mathbf {x}},t)\mapsto ({\mathbf {x}}+t{\mathbf {v}},t)} ，其中 v 在 R 内。平移表达为 ( x , t ) ↦ ↦ --> ( x + a , t + b ) {\displaystyle ({\mathbf {x}},t)\mapsto ({\mathbf {x}}+{\mathbf {a}},t+b)} ，其中 a 在 R 内， b 在 R 内。旋转表达为 ( x , t ) ↦ ↦ --> ( G x , t ) {\displaystyle ({\mathbf {x}},t)\mapsto (G{\mathbf {x}},t)} ，其中 G : R → R 为某正交李群。 作为一个李群，伽利略变换的维度为10。

伽利略群的中心扩张

这里我们只考虑伽利略群的李代数。结果能够轻易延伸到李群。L的李代数由H、P i 、C i 和L ij 张成（反对称张量），并能够受交换子的作用，其中

H为时间平移的生成元（哈密顿算符），P i 为平移的生成元（动量算符），C i 为伽利略变换的生成元，而L ij 为旋转的生成元（角动量算符）。

现在我们可以对H"、P" i 、C" i 、L" ij （反对称张量）、M所张成的李群进行中心扩张，使得M与一切都可交换（位于中心，“中心扩张”因此得名）：

参见

洛伦兹群

庞加莱群

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。