定义和直接的结果

一个实向量丛要包含下列空间跟映射：

X（基空间(base space)）和E（全空间(total space)）为拓扑空间(或是流形等其他空间)

一个连续满射π : E → X（称作投影）

对 X 中的每个 x，π（{x}）是有限维的实向量空间(称作纤维(fiber) )。

且这些空间跟映射要满足以下相容性条件：对 X 中的每一点有一个开邻域 U⊆ ⊆ -->X{\displaystyle U\subseteq X} 包含这点，一个自然数n,同胚个同胚

使得:

(π π -->∘ ∘ -->φ φ -->)(x,v)=x{\displaystyle (\pi \circ \varphi )(x,v)=x} 对所有 x ∈ U，v ∈ R均成立

固定 x，映射　v↦ ↦ -->φ φ -->(x,v){\displaystyle v\mapsto \varphi (x,v)}　是两个向量空间 R 和 π（{x}）之间的线性同构，这对每点 x ∈ U 都成立。

开邻域U和同胚φ合起来叫做丛的局部平凡化。这表示映射π在局部看起来"像" U × R到U 上的投影.

向量丛 X × R 称为平凡，如果赋予这空间一个投影映射　X × R → X，也就是 E=X × R 整体上是 X 的乘积空间 。

每个纤维π（{x}）是一个有限维实向量空间，所以有在点 x 有一个维数dx，由局部平凡化的性质可知函数　x↦ ↦ -->dx{\displaystyle \textstyle x\mapsto d_{x}} 在局部上是常数，也就是它在X　的每个连通的部分上为常数。如果它在X上是常数的话，我们把这个维数叫做向量丛的阶。一阶向量丛也叫线丛。

向量丛态射

一个从向量丛π1 : E1 → X1到向量丛π2 : E2 → X2的态射（morphism）是一对连续映射f : E1 → E2和g : X1 → X2使得

gπ1 = π2f

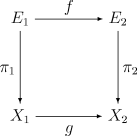
对于每个X1中的x,由f诱导的映射π1({x}) → π2({g(x)})是一个向量空间的线性变换。

所有向量丛的类和丛的射组成了一个范畴。限制到光滑流形和光滑丛射，我们就有了光滑向量丛的范畴。

我们可以考虑有一个固定基空间X的所有向量丛组成的范畴。我们取那些在基空间X上为恒等映射（identity map）的射作为在这个范畴中的射. 也就是说，丛射满足下面的交换图：

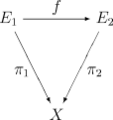
（注意这个范畴不是可交换的；向量丛的射的核通常不能很自然的成为一个向量丛。）

截面和局部自由层

给定一个向量丛π : E → X和一个开子集U,我们可以考虑π在U上的截面,也就是连续函数s : U → E满足πs = idU.本质上，截面给U的每一点一个从附在该点的向量空间中所取的向量，取值要有连续性。

例如，微分流形的切丛的截面就是流形上的向量场。

令F(U)为U上所有截面的集合. F(U)总有至少一个元素：把V中的x映射到π（{x}）的零元的函数s.使用每点的加法和数乘，F(U)本身也成为了向量空间.这些向量空间的总和就是X上的向量空间的层。

若s属于F(U)而α : U → R是一连续映射，则αs属于F(U).我们可以看到F(U)是一个U上的连续实值函数的环上的模.进一步讲，若OX表示X上连续函数的层结构，则F是OX-模的一个层.

不是OX-模的每个层都是以这种方式从向量丛的导的：只有局部自由层可以从这种方法得到。（理由：局部的，我们要找一个投影U × R → U的一个截面，这些恰好是连续函数U → R,并且这一函数是连续函数U → Rn-元组.）

更进一步讲：X上的实向量丛的范畴是等价于OX-模的局部自由和有限生成的层的。

所以我们可以将向量丛视为位于OX-模的层的范畴内；而后者是可交换的，所以我们可以计算向量丛的射的核。

向量丛上的操作

两个X上的在同一个域上的向量丛，有一个惠特尼和,在每点的纤维为那两个丛的纤维的直积。同样，纤维向量积和对偶空间丛也可以这样引入。

变种和推广

向量丛是纤维丛的特例。

光滑向量丛定义为满足E和X是光滑流形，π : E → X是光滑映射，而局部平凡化映射φ是微分同胚的向量丛。

把实向量空间换成复的，就得到了复向量丛。这是结构群的约化的特例。也可以用其他拓扑域上的向量空间，但相对比较少见。

如果我们允许在局部平凡化中使用任意巴拿赫空间（而不仅是R），就可以得到巴拿赫丛.

参考

Milnor, John W.; Stasheff, James D. Characteristic classes. Annals of Mathematics Studies, No. 76. Princeton University Press, Princeton, N. J.; University of Tokyo Press, Tokyo, 1974. vii+331 pp. ISBN 0-691-08122-0.

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。