动机

让·勒雷当初为了研究代数拓扑学，而引入层的概念，从而面临计算层上同调的问题。为此，勒雷发明了现称勒雷谱序列的计算方法，它联系了一个层的上同调群与其正像的上同调群。

人们很快就发现：勒雷谱序列只是一个特例。谱序列还现身于纤维化等几何问题；更抽象地说，对合成函子取导函子也会得到谱序列，称为格罗滕迪克谱序列。虽然导范畴在理论层面提供了较简炼的框架，谱序列仍是最有效的计算工具。

由于谱序列包含大量的项，实际计算时往往会陷入带（至少）三重指标的群或模的迷阵。在许多实际状况中，谱序列最后会“塌陷”，此时谱序列可以给出明确的资讯。若谱序列不塌陷，则须靠一些窍门取得有用的资讯。

形式定义

以下固定一个阿贝尔范畴 A {\displaystyle {\mathcal {A}}} ，常见例子是一个环上的模范畴。谱序列是一个非负整数 r 0 {\displaystyle r_{0}} 及下述资料：

对所有整数 r ≥ ≥ --> r 0 {\displaystyle r\geq r_{0}} ，有范畴中的一个对象 E r {\displaystyle E_{r}} 。

自同态 d r : E r → → --> E r {\displaystyle d_{r}:E_{r}\to E_{r}} ，满足 d r 2 = 0 {\displaystyle d_{r}^{2}=0} ，称为边界映射或微分。

从 E r + 1 {\displaystyle E_{r+1}} 到 H ( E r , d r ) {\displaystyle H(E_{r},d_{r})} 的同构。

通常省去 E r + 1 {\displaystyle E_{r+1}} 与 H ( E r , d r ) {\displaystyle H(E_{r},d_{r})} 的同构，而写成等式。

最基本的例子是链复形 C ∙ ∙ --> {\displaystyle C_{\bullet }} ，它带有一个微分 d {\displaystyle d} 。取 r 0 = 0 {\displaystyle r_{0}=0} ，并令 E 0 = C ∙ ∙ --> {\displaystyle E_{0}=C_{\bullet }} ，于是必有 E 1 = H ( C ∙ ∙ --> ) {\displaystyle E_{1}=H(C_{\bullet })} ；这个新链复形上的微分只有一个自然的选择，就是零映射。于是有 E 1 = E 2 = ⋯ ⋯ --> {\displaystyle E_{1}=E_{2}=\cdots } 。综之，我们得到一个链复形范畴上的谱序列：

E 0 = C ∙ ∙ --> {\displaystyle E_{0}=C_{\bullet }}

E r = H ( C ∙ ∙ --> ) ( r ≥ ≥ --> 1 ) {\displaystyle E_{r}=H(C_{\bullet })\;(r\geq 1)}

由于只有 r = 0 {\displaystyle r=0} 时微分映射才可能非零，此序列在第一步后就不含任何新资讯。

较常见的是双分次模（或层）范畴上的谱序列，表作 E r p , q {\displaystyle E_{r}^{p,q}} ，此时的微分映射次数与 r {\displaystyle r} 有关：对于上同调谱序列， d r : E r → → --> E r {\displaystyle d_{r}:E_{r}\to E_{r}} 的次数是 ( r , − − --> r + 1 ) {\displaystyle (r,-r+1)} 。对于同调谱序列，通常将各项写成 E r {\displaystyle E_{r}} ，微分映射 d r : E r → → --> E r {\displaystyle d^{r}:E_{r}\to E_{r}} 的次数是 ( − − --> r , r − − --> 1 ) {\displaystyle (-r,r-1)} 。

谱序列之间的态射 f : E → → --> E ′ {\displaystyle f:E\to E"} 定义为一族态射 f r : E r → → --> E r ′ {\displaystyle f_{r}:E_{r}\to E_{r}"} ，使之与同构 E r + 1 ≃ ≃ --> H ( E r , d r ) {\displaystyle E_{r+1}\simeq H(E_{r},d_{r})} 交换。谱序列对此构成了一个阿贝尔范畴。

正合偶

交换代数中大部分的谱序列来自链复形，而已知构造谱序列最有力的方法是 William Massey 的正合偶。正合偶在代数拓扑学中很常见，此时对于许多谱序列，正合偶是唯一已知的构造法。事实上，正合偶可以用来构造所有已知的谱序列。

同样固定一个阿贝尔范畴（通常取一个环上的双分次模） A {\displaystyle {\mathcal {A}}} ，一个正合偶是：

一对对象 A , C {\displaystyle A,C}

三个态射：

使之满足下述正合条件：

Image f = Kernel g

Image g = Kernel h

Image h = Kernel f

将这组资料简记为 ( A , C , f , g , h ) {\displaystyle (A,C,f,g,h)} 。正合偶通常以三角形表示。 C {\displaystyle C} 对应到谱序列的 E 0 {\displaystyle E_{0}} 项，而 A {\displaystyle A} 是一些辅助资料。

为了得到谱序列的后续项，以下将构造导出偶。令：

d := g ∘ ∘ --> h {\displaystyle d:=g\circ h}

A ′ := f ( A ) {\displaystyle A":=f(A)}

C ′ := K e r ( d ) / I m ( d ) {\displaystyle C":=\mathrm {Ker} (d)/\mathrm {Im} (d)}

f ′ := f | A ′ {\displaystyle f":=f|_{A"}}

h ′ : C ′ → → --> A ′ {\displaystyle h":C"\to A"} 由 h {\displaystyle h} 导出。

g ′ : A ′ → → --> C ′ {\displaystyle g":A"\to C"} 定义如下：若 A {\displaystyle {\mathcal {A}}} 为某个环上的模范畴，对任一 a ∈ ∈ --> A ′ {\displaystyle a\in A"} ，存在 b ∈ ∈ --> A ′ {\displaystyle b\in A"} 使得 a = f ( b ) {\displaystyle a=f(b)} ，定义 g ′ ( a ) {\displaystyle g"(a)} 为 g ( b ) {\displaystyle g(b)} 在 C ′ {\displaystyle C"} 中的像。一般而言，可利用 Mitchell 嵌入定理构造态射 g ′ {\displaystyle g"} 。

现在可以验证 ( A ′ , C ′ , f ′ , g ′ , h ′ ) {\displaystyle (A",C",f",g",h")} 构成正合偶。 C ′ {\displaystyle C"} 对应到谱序列的 E 1 {\displaystyle E_{1}} 项。续行此法，可以得到一族正合偶 ( A ( n ) , C ( n ) , f ( n ) , g ( n ) , h ( n ) ) {\displaystyle (A^{(n)},C^{(n)},f^{(n)},g^{(n)},h^{(n)})} 。相应的谱序列定义为 E n := C ( n ) {\displaystyle E_{n}:=C^{(n)}} ， d n := g ( n ) ∘ ∘ --> h ( n ) {\displaystyle d_{n}:=g^{(n)}\circ h^{(n)}} 。

图解

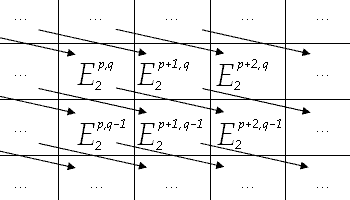
谱序列的 E2 项

一个双分次谱序列含有大量要追踪的资讯，不过有个常见的图解法有助于阐明其结构。以下取上同调谱序列为例。在此有三个指标 r , p , q {\displaystyle r,p,q} 。对每个 r {\displaystyle r} ，设想有一张方格纸，分别让 p , q {\displaystyle p,q} 对应于横、纵轴。每一个格子点 ( p , q ) {\displaystyle (p,q)} 对应到对象 E r p , q {\displaystyle E_{r}^{p,q}} 。微分 d r {\displaystyle d_{r}} 的次数为 ( r , − − --> r + 1 ) {\displaystyle (r,-r+1)} ，方向如图所示。

收敛与退化

在第一个简单的例子中，谱序列在 r ≥ ≥ --> 1 {\displaystyle r\geq 1} 后的微分映射皆为零，故不再改变。这时可定义该谱序列的极限为 E ∞ ∞ --> := E r ( r ≥ ≥ --> 1 ) {\displaystyle E_{\infty }:=E_{r}\;(r\geq 1)} 。对于一般的谱序列，也往往存在一个极限，极限与各项的关系可说是谱序列的众妙之门。

定义：若谱序列 E r p , q {\displaystyle E_{r}^{p,q}} 对每个 ( p , q ) {\displaystyle (p,q)} 都存在 r ( p , q ) ∈ ∈ --> N {\displaystyle r(p,q)\in \mathbb {N} } ，使得当 r ≥ ≥ --> r ( p , q ) {\displaystyle r\geq r(p,q)} 时， d r p − − --> r , q + r − − --> 1 : E r p − − --> r , q + r − − --> 1 → → --> E r p , q {\displaystyle d_{r}^{p-r,q+r-1}:E_{r}^{p-r,q+r-1}\to E_{r}^{p,q}} 及 d r p , q : E r p , q → → --> E r p + r , q − − --> r + 1 {\displaystyle d_{r}^{p,q}:E_{r}^{p,q}\to E_{r}^{p+r,q-r+1}} 皆为零，则称 E r p , q {\displaystyle E_{r}^{p,q}} 之极限项为 E ∞ ∞ --> p , q := E r p , q {\displaystyle E_{\infty }^{p,q}:=E_{r}^{p,q}} （取充分大的 r {\displaystyle r} ）。最常见的例子是集中在第一象限的谱序列，此时极限项恒存在。

其中的指标 p {\displaystyle p} 指涉过滤结构。

若存在对象 E ∙ ∙ --> {\displaystyle E^{\bullet }} 、过滤结构 ⋯ ⋯ --> ⊂ ⊂ --> F p + 1 E ∙ ∙ --> ⊂ ⊂ --> F p E ∙ ∙ --> ⊂ ⊂ --> ⋯ ⋯ --> {\displaystyle \cdots \subset F^{p+1}E^{\bullet }\subset F^{p}E^{\bullet }\subset \cdots } ，及一族同构 β β --> p , q : E ∞ ∞ --> p , q ≃ ≃ --> g r p E p + q {\displaystyle \beta ^{p,q}:E_{\infty }^{p,q}\simeq \mathrm {gr} ^{p}E^{p+q}} ，满足 ⋂ ⋂ --> p F p E ∙ ∙ --> = ( 0 ) , ⋃ ⋃ --> p F p E ∙ ∙ --> = E ∙ ∙ --> {\displaystyle \bigcap _{p}F^{p}E^{\bullet }=(0),\bigcup _{p}F^{p}E^{\bullet }=E^{\bullet }} （这种过滤称为“正则过滤”），则称 E r p , q {\displaystyle E_{r}^{p,q}} 收敛到 E ∙ ∙ --> {\displaystyle E^{\bullet }} ，通常表为下述符号：

习惯上，人们也常将左式写成 E 2 p , q {\displaystyle E_{2}^{p,q}} ，因为谱序列中最重要的页往往是 E 2 p , q {\displaystyle E_{2}^{p,q}} 。

最简单的收敛特例是退化：

定义：固定 r ∈ ∈ --> N {\displaystyle r\in \mathbb {N} } ，若对每个 s ≥ ≥ --> r {\displaystyle s\geq r} ，微分映射 d s {\displaystyle d_{s}} 都是零，则称该谱序列在第 r {\displaystyle r} 页退化。

退化性保证了 E r ≃ ≃ --> E r + 1 ≃ ≃ --> ⋯ ⋯ --> {\displaystyle E_{r}\simeq E_{r+1}\simeq \cdots } ，此时 E r {\displaystyle E_{r}} 即其极限。如果一个双分次谱序列 E r p , q {\displaystyle E_{r}^{p,q}} 的非零项集中于某一条水平或垂直线上，则必在 r = 2 {\displaystyle r=2} 时退化。

例子

过滤结构导出的谱序列

最常见的谱序列之一来自带有过滤结构的对象，通常是链复形或上链复形。这是一个对象 C {\displaystyle C} 及微分映射 d : C → → --> C {\displaystyle d:C\to C} ，使之满足 d 2 = 0 {\displaystyle d^{2}=0} ，以及

同调群上也有相应的过滤

对此，定义相应的分次对象

取微分映射为零，可视之为复形。

以下式定义谱序列：

此时有 E 0 p = F p C / F p + 1 C , E 1 p = H ( g r p C ) {\displaystyle E_{0}^{p}=F^{p}C/F^{p+1}C,E_{1}^{p}=H(\mathrm {gr} ^{p}C)} ，且谱序列收敛：

通常也写成 E r ⇒ ⇒ --> H ( C ) {\displaystyle E_{r}\Rightarrow H(C)} 。

取 A {\displaystyle {\mathcal {A}}} 为取值在某个阿贝尔范畴中的上链复形范畴。此时的对象 C {\displaystyle C} 是个上链复形 ⋯ ⋯ --> → → --> C q → → --> C q + 1 → → --> ⋯ ⋯ --> {\displaystyle \cdots \to C^{q}\to C^{q+1}\to \cdots } ， d {\displaystyle d} 是上链复形的微分映射。上述谱序列带有三个指标 p , q , r {\displaystyle p,q,r} ，并可进一步化成下述形式：

双复形的谱序列

以下考虑取值在某个阿贝尔范畴中的双复形，即一组对象 C p , q {\displaystyle C^{p,q}} ，及两组微分映射 d ′ : C p , q → → --> C p + 1 , q {\displaystyle d":C^{p,q}\to C^{p+1,q}} 及 d ″ : C p , q → → --> C p , q + 1 {\displaystyle d"":C^{p,q}\to C^{p,q+1}} ，满足

对一个双复形，可定义其全复形 ( C , D ) {\displaystyle (C,D)} （也记为 T ( C ) {\displaystyle T(C)} 或 T o t ( C ) {\displaystyle \mathrm {Tot} (C)} ） 为

C {\displaystyle C} 上有两组过滤，分别是：

它们给出两个谱序列 ′ E r {\displaystyle "E_{r}} 与 ″ E r {\displaystyle ""E_{r}} 。首先计算 ′ E 0 , ′ E 1 , ′ E 2 {\displaystyle "E_{0},"E_{1},"E_{2}} 项：

同理可计算 ″ E 0 , ″ E 1 , ″ E 2 {\displaystyle ""E_{0},""E_{1},""E_{2}} ：

这两个谱序列通常是不同的，但随着 r {\displaystyle r} 增大，它们都收敛到 H ( C ) {\displaystyle H(C)} ，由此可以得到一些有趣的比较定理。

例子

Tor函子的交换性

利用谱序列，可以迅速导出Tor函子的交换性，即一自然同构：

取定平坦分解 P ∙ ∙ --> → → --> M → → --> 0 {\displaystyle P_{\bullet }\to M\to 0} 及 Q ∙ ∙ --> → → --> N → → --> 0 {\displaystyle Q_{\bullet }\to N\to 0} 。视之为集中于正项的复形，其微分映射分别记为 d , e {\displaystyle d,e} 。考虑双复形 C i , j := P i ⊗ ⊗ --> Q j {\displaystyle C_{i,j}:=P_{i}\otimes Q_{j}} ，其微分映射定义为 d i , j := d i ⊗ ⊗ --> i d + ( − − --> 1 ) j i d ⊗ ⊗ --> e j {\displaystyle d_{i,j}:=d_{i}\otimes \mathrm {id} +(-1)^{j}\mathrm {id} \otimes e_{j}} （以使微分映射满足反交换性）。取其谱序列，遂得到：

由于复形 P ∙ ∙ --> , Q ∙ ∙ --> {\displaystyle P_{\bullet },Q_{\bullet }} 是平坦分解，其同调群只集中在零次项，此时其表示式为：

故 ′ E p , q 2 {\displaystyle "E_{p,q}^{2}} 只在 p = 0 {\displaystyle p=0} 上有非零项，而 ″ E p , q 2 {\displaystyle ""E_{p,q}^{2}} 只在 q = 0 {\displaystyle q=0} 上有非零项，这保证了谱序列在第二页退化，由此导出同构：

当 p = q {\displaystyle p=q} 时，上述等式的右项同构（虽然其分次结构不同），由此得到 Tor 的交换性。

示性数

运用谱序列时，通常会假设某些项为零，或假设谱序列在第一或第二页退化。但有时尽管对各项及微分映射一无所知，仍可从谱序列中萃取资讯，最简单的例子是示性数：固定一个阿贝尔范畴 A {\displaystyle {\mathcal {A}}} 及一个交换群 C {\displaystyle C} ，所谓示性数是一个函数 χ χ --> : O b A → → --> C {\displaystyle \chi :\mathrm {Ob} {\mathcal {A}}\to C} ，满足：

∀ ∀ --> 0 → → --> Y → → --> X , χ χ --> ( X ) = χ χ --> ( Y ) + χ χ --> ( X / Y ) {\displaystyle \forall 0\to Y\to X,\;\chi (X)=\chi (Y)+\chi (X/Y)}

X ≃ ≃ --> Y ⇒ ⇒ --> χ χ --> ( X ) = χ χ --> ( Y ) {\displaystyle X\simeq Y\Rightarrow \chi (X)=\chi (Y)}

例如：取 A {\displaystyle {\mathcal {A}}} 为某个域 k {\displaystyle k} 上的有限维向量空间范畴，则 χ χ --> : V ↦ ↦ --> dim k ⁡ ⁡ --> V {\displaystyle \chi :V\mapsto \dim _{k}V} 是一个示性数。

对任一 A {\displaystyle {\mathcal {A}}} 上的有限复形 K ∙ ∙ --> {\displaystyle K^{\bullet }} ，定义

容易证明 χ χ --> ( K ∙ ∙ --> ) = ∑ ∑ --> i ( − − --> 1 ) i χ χ --> ( H i ( K ∙ ∙ --> ) ) {\displaystyle \chi (K^{\bullet })=\sum _{i}(-1)^{i}\chi (H^{i}(K^{\bullet }))} 。考虑任一在 A {\displaystyle {\mathcal {A}}} 上的收敛谱序列 ( E r ∙ ∙ --> ) {\displaystyle (E_{r}^{\bullet })} ，由于谱序列的每一页都是前一页的同调，遂得到

然而

于是得到

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。