综述

  物质的质量极大地影响许多常见的动力学性质。

在自然科学外, 一般情况下，质量用以描述某物有多“重”。然而, 事实上质量描述物体的惯性; 也就是说, 物体在不受外力下保持匀速运动的趋势。根据牛顿运动定律以及牛顿本人的研究结果总结出来的公式F = m""a,，质量m为1kg的物体在受到1N的力时，获得的加速度是1 m s(约是重量加速度的10.2%)。

观察保龄球的球瓶在光滑的水平面上被保龄球推倒，可以体会惯性的存在。球瓶受到的水平的推力, 与保龄球的方向为向下的重力 － 体现为必须对其施力才能使其离开地面 － 完全不同。另外, 值得注意的是, 在月球上的引力是地球上的六分之一, 而物体的质量却保持不变; 尽管“反冲动力学”(质量、速度、惯性、“弹性碰撞”与“非弹性碰撞”)的因素占有统治地位, 而引力的因素显得微不足道, 却物体的行为没有很大的变化。例如同样地在月球上打桌球, 球反弹的速度与在地球上并无二致; 唯一的区别是, 球落入球袋的速率慢了许多。

为了使计算清晰而精确, 在自然科学中, “质量”和“重量”各自有不同的严格定义。但在自然科学外的使用中, 地球上大多数质量都有其重量, 且两者几乎成正比例关系, 两者也因此常用“重量”一词统称，具体含义则视语境而定。例如，在商业中，零售产品的“净重”通常指质量, 用千克或磅为单位表示。相反, 汽车轮胎上标识的、说明轮胎最大“结构荷重”的“载重指数”所指的是重量，即由于引力作用而受到的力。在20世纪后期之前，两者的区别不如现在严格, 甚至在科技写作中也是如此, 以至于至今仍然可以看到将“分子质量”误作“分子重量”等的写法。

因为质量和重量是不同的量, 它们各有不同的计量单位。在国际单位制(SI)中,kg是质量单位, 而N则是力的单位。非SI单位千克力也被用作测量重量。相似地,常衡制中的磅是质量单位, 而其对应的力的单位则是磅力。

质量与地球上的等效力间的单位转化

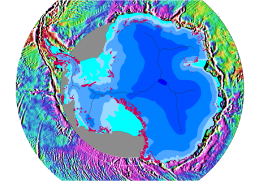
  这幅假色地形图展示了南半球海洋的重力异常。在这幅图中，由纬度差异造成的引力变化已经经过修正。

当我们用千克来表示一个物体的重量（即其所受的地心引力）时, 所用到的测量单位并不是真正意义上的千克，而是千克力(kgf或kg-f, 有时也用kp表示, 源自英语中千克力的另一个名称kilopond)。千克力是一个力的非国际单位制单位。地球上所有物体都受到大约值为9.81 m s的重力加速度。“国际度量衡大会”(General Conference on Weights and Measures)将标准重力的精确值修正为{{nowrap 9.80665 m s}}, 以便如度量衡学等学科在将单位从转换质量到力和压强时有一个标准值供使用。事实上, 千克力的就以牛顿定义, 精确值就是9.80665牛顿。实际操作上, 重力加速度(符号: g)的数值随着纬度、海拔以及地表下岩石的密度的不同, 自身也有些微的差别, 但这些差别通常只有千分之几。

工程学以及其它涉及加速度和动能的科学分支的专业人员, 对质量、力和重量的概念区分得很严谨, 对这些量的测量单位也是如此。涉及到结构荷重(一个结构由于引力所受的力)的学科(如结构工程学)的工程人员, 出于研究如混凝土和汽车等物体的目的, 首先尝试了将荷重的单位 − 为记录方便起见，通常为千克 − 转化到牛顿，以便继续计算。进行单位转换，是因为许多的关于材料性质的常数，例如弹性系数, 都是以牛顿和帕斯卡(一个从源自牛顿的单位)为单位来测量和发表的。在实践的工程应用中, 以千克表示的质量被转化成以牛顿表示重量时, 数值上要乘以标准重力的值9.80665。

浮力和重量

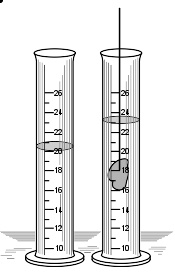
  无论浸没物体的是何种流体(气体或液体), 物体所受的浮力都等于它所排开的流体的重量。

  当一个热气球拥有中性浮力时, 它周围的人并不需费力支持它的重量, 但它却仍然保持它巨大的质量和惯性。

通常情况下质量跟重量几乎呈正比例关系；质量是一瓶体积为一升的汽水100倍的物体，称量起来也是汽水的100倍——大约1000牛顿。然而情况并非永远如此，许多人们熟悉的事物经常违反质量 / 重量的比例。

氦气球对许多儿童而言并不陌生。一个满胀的氦气球会拥有浮力——一种方向与引力相反的力。当氦气球泄露了一定量的氦气时，往往有某个时刻，它会处于悬浮状态——既不上升，也不下降，并且——单纯就用计重秤对其称重而言——处于完全失重的状态。尽管组成气球的橡胶的质量往往被忽略不计，但在充气膨胀后，橡胶的质量没有任何变化。在这里，氦气球没有重量，但有质量。

浮力不仅仅只对气球起作用；当地球上具有一定尺寸的物体被浸没在流体（自然科学中液体和气体的统称）中时都受到不同程度的浮力。无论是对泳池中漂浮的游泳者，还是在空气中漂浮的热气球而言，浮力可以完全抵消物体的重量，从而使物体“失重”。

热气球模型可能有助更好地理解“失重”（悬浮）气球的质量。尽管热气球在地面上方盘旋时不需额外的力量支撑，由热气球那可观的质量造成的惯性却可以轻易地将地面上的成年人击倒。

浮力对浮体的作用遵循阿基米德原理。与在低引力环境对物体重量的影响相比，浮力不值一提——它并没有使物体的重量“消失”，只是将其“转移”。以浸在泳池里的人为例，他“失去”的重量只是由泳池底承受，而使得在水底的计重秤承受了较轻的重量罢了。然而如果称量整个水池，就会发现浸没在其中的人的重量完全被由水池承受，而最终就会显示在计重秤上。也就是说，尽管将物体浸在流体中称重的结果会较轻，但物体—流体系统的重量在将物体浸入之后却有增无减。由于空气也是流体，浮力定律同样应用于物体—空气系统——空气通过浮力承受了物体的一部分重量，并最终将其转嫁到大地之上。因此，严格来说，由于大气的存在，人们在地球上所称得自己的体重，都比实际体重为轻。

一般而言，空气浮力对具有一般密度的物体而言，作用过于微小，在自然科学外都可忽略不计。以称体重为例，人体所受浮力大约是所受引力的1/860。 此外，不同地区气压的差异对体重称量值造成的影响不超过±1/30,000。不过, 在度量衡学中, 由于校正实验室的量器所用到的标准砝码的精确度很高，空气密度导致的浮力效应会造成一定影响。实际操作中所用的砝码，是根据由铂铱合金制作的标准砝码(如存放在法国的“国际千克原器”), 用特殊的不锈钢合金制得，密度为8,000 kg/m。这种砝码的体积比铂铱合金（密度为21,550 kg/m）要大。为方便起见，在使用不锈钢砝码进行度量时，人们发展出了“惯用质量”的概念, 其定义为: “在20°C时, 物体在密度为1.2 kg m的空气中, 所平衡的密度为8 000 kg m的砝码的质量”。对于不锈钢材料, 其惯用质量比真实质量轻150ppm; 因此砝码在制造时会经过适当的修正, 使其真实质量与标示的质量一致。

在实验室用不锈钢砝码校准量器后，量器所称量的实际上是物体的惯用质量，即真实质量减去150ppm的浮力。不同物体的密度不尽相同，就算质量恰好相等，由于所占空间的体积不一样，它们的重量和所受的浮力也不一样，所以在上述的、经不锈钢砝码校准的量器上称出的（通过与不锈钢砝码比较），只是该物体的惯用质量，也就是其真实质量减去该物体的浮力，而这个浮力却又是未知。在高精度的实验中，必须测量待测物体的体积，在后期处理时计算它所受的浮力，从而得到物体的真实质量。

不同种类的秤以及其测量值

  一个天平式计重秤：测量值不受引力强度影响

  基于传感器的浴室磅秤：测量值受到引力强度影响

严格来说，在任何情况下，医院的天平式计重秤所称量的都是物体的质量。这是因为天平（“双盘”式质量比较仪）在比较平台上的重量和在秤杆上滑动的平衡物的重量；引力只是作为一个力的发生器，从而使得指针可以偏离“平衡”点而显示比较结果。用天平在地球的赤道和两极称量同一物体的质量，误差不超过0.3%；可以说，天平对地心引力以及地球沿地轴自转所产生的离心力“免疫”。

相反，在任何情况下，弹簧秤或基于传感器的数字秤（单盘设备）所称量的都是物体的重量。像这类测力计，引力强度的变化直接影响读数。实际操作中，当测力的计重秤应用在商业或者医学中时，这些秤都必须在现场校准，从而在一定的精确范围内称量出用磅或千克表示的物体质量。

参见

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。