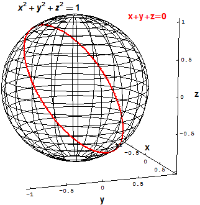
联立多项式的零点球和倾斜的圆周在古典代数几何中，主要的研究对象是一组多项式的公共零点集，即同时满足一个或多个多项式方程的所有点组成的集合。例如，在三维欧几里德空间R3{\displaystyle\mathbb{R}^{3}}中的单位球面被定义为满足方程的所有点(x,y,z){\displaystyle(x,y,z)}的集合。一个"倾斜的"圆周在三维欧几里德空间R3{\displaystyle\mathbb{R}^{3}}中可以被定义为同时满足如下两个方程的所有点(x,y,z){\displaystyle(x,y,z)}的集合。仿射簇现在我们开始进入稍微抽象的领域。考虑一个数域k，在古典代数几何中这个域通常是复数域C，现在我们把它推广为一个代数封闭的数域。我们定义数域k上的n维仿射空间Akn{\displaystyle{\mathbb{A}}_{k}^{n}}，简单讲来，它只是一些点的集合，...

定义设A{\displaystyleA}为一交换环，A{\displaystyleA}上的代数（或称A{\displaystyleA}-代数）是下述结构：集合E{\displaystyleE}是个A{\displaystyleA}-模。指定E{\displaystyleE}上的一个二元运算，通常以乘法符号表示：此二元运算是双线性的，换言之：最常考虑的情形是A{\displaystyleA}是一个域，这时称域代数，一些作者也将代数定义成域上的代数。若E{\displaystyleE}上的乘法满换性xy=yx{\displaystylexy=yx}，则称之为可交换代数；若E{\displaystyleE}上的乘法满足结合律x(yz)=(xy)z{\displaystylex(yz)=(xy)z}，则称之为结合代数，详阅主条目结合代数。交换代数学中考虑的代数均属可交换的结合代数。代数同态设E,F...

历史希腊数学家欧几里得在其著作几何原本中详述几何性的代数。代数的起源可以追溯到古巴比伦的时代，当时的人们发展出了较之前更进步的算术系统，使其能以代数的方法来做计算。经由此系统的被使用，他们能够列出含有未知数的方程并求解，这些问题在今日一般是使用线性方程、二次方程和不定线性方程等方法来解答的。相对地，这一时期大多数的埃及人及公元前1世纪大多数的印度、希腊和中国等数学家则一般是以几何方法来解答此类问题的，如在莱因德数学纸草书、绳法经、几何原本及九章算术等书中所描述的一般。希腊在几何上的工作，以几何原本为其经典，提供了一个将解特定问题解答的公式广义化成描述及解答方程之更一般的系统之架构。代数（algebra）导源于阿拉伯语单字“al-jabr”，其出自al-Kitābal-muḫtaṣarfīḥisābal-ğabrwa-l-muqābala这本书的书名上，意指移项和合并同类项之计算的摘要，其为...

基本构思从泛代数角度来看，代数是个集合A拥有一组算子。在A上的一个n元运算是个函数以n个A的元素为输入并返回一个A的元素。无元运算：产生常数a单元运算：例如~x二元运算：x*y除了运算，还有符合一些公理及方程式定律，例如结合律、交换律等等。相关条目调和分析测度分析微分几何及拓扑代数拓扑代数几何抽象代数

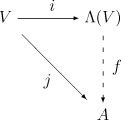
定义及运算律外代数有很多种等价的定义，下面的定义是最简洁的一个。定义:设V{\displaystyleV}是域K{\displaystyleK}上的一个向量空间，让Tk(V):=V⊗⊗-->⋯⋯-->⊗⊗-->V⏟⏟-->k{\displaystyleT^{k}(V):={\underset{k}{\underbrace{V\otimes\cdots\otimesV}}}}则定义令I{\displaystyleI}为V{\displaystyleV}的张量代数的理想（即双边理想），该理想是由所有形如v⊗⊗-->v{\displaystylev\otimesv}的张量生成的（其中v∈∈-->V{\displaystylev\inV}任意），则将V{\displaystyleV}上的外代数ΛΛ-->(V){\displaystyle\Lambda(V)...