三角形的重心坐标

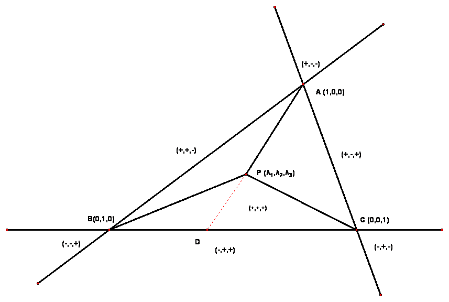
在三角形情形中，重心坐标也叫面积坐标，因为P点关于三角形ABC的重心坐标和三角形PBC, PCA及PAB的（有向）面积成比例，证明如下（如右图所示）。

我们用黑体小写字母表示对应点的向量，比如三角形ABC顶点为a,b{\displaystyle {\textbf {a}}\,,{\textbf {b}}\,}和c{\displaystyle {\textbf {c}}\,}，P点为p{\displaystyle {\textbf {p}}}等。设PBC, PCA及PAB面积之比为λ λ -->1:λ λ -->2:λ λ -->3{\displaystyle \lambda _{1}:\lambda _{2}:\lambda _{3}\,}且λ λ -->1+λ λ -->2+λ λ -->3=1{\displaystyle \lambda _{1}+\lambda _{2}+\lambda _{3}=1}，设射线AP与BC交于D，则

所以，(λ λ -->1,λ λ -->2,λ λ -->3){\displaystyle (\lambda _{1},\lambda _{2},\lambda _{3})}就是P的重心坐标。

坐标变换

给定三角形平面一点P，我们将这一点的面积坐标λ λ -->1{\displaystyle \lambda _{1}\,}，λ λ -->2{\displaystyle \lambda _{2}\,}和λ λ -->3{\displaystyle \lambda _{3}\,}用笛卡尔坐标表示出来。

利用笛卡尔坐标中的三角形面积公式：

我们可得：

类似地有λ λ -->2,λ λ -->3{\displaystyle \lambda _{2},\lambda _{3}}，注意ABC构成一个三角形，上式的分母不可能为0。

反过来则简单得多：

判断一点的位置

因重心坐标是笛卡尔坐标的一个线性变换，从而它们在边和三角形区域之间的变化是线性的。如果点在三角形内部，那么所有重心坐标属于开区间(0,1){\displaystyle (0,1)}；如果一点在三角形的边上，至少有一个面积坐标λ λ -->1...3{\displaystyle \lambda _{1...3}}为0，其余分量位于闭区间[0,1]{\displaystyle [0,1]}。如果有某个坐标小于0，则位于三角形外部，具体分布可参考上图。 （图示中，B和C顶端的坐标正副反了，B的应该是（-,-,+），C的是（-,+,-）

应用

面积坐标在涉及到三角形子区域的工程学问题时特别有用，经常可以化简解析积分求值，高斯积分法表也常以面积坐标的形式给出。

考虑由顶点v1{\displaystyle {\textbf {v}}_{1}\,}, v2{\displaystyle {\textbf {v}}_{2}\,}和v3{\displaystyle {\textbf {v}}_{3}\,}定义的三角形T，任何在三角形内部的点p{\displaystyle {\textbf {p}}}都能写成顶点的加权和：

这里λ λ -->1{\displaystyle \lambda _{1}\,}、λ λ -->2{\displaystyle \lambda _{2}\,}和λ λ -->3{\displaystyle \lambda _{3}\,}是面积坐标。注意到λ λ -->3=1− − -->λ λ -->1− − -->λ λ -->2{\displaystyle \lambda _{3}=1-\lambda _{1}-\lambda _{2}\,}。从而，函数f{\displaystyle f}在T上的积分为：

这里S是三角形T的面积。注意上式具有线性插值的形式。

重心坐标提供了一种非结构网格上函数插值的方法，假设函数值在所有网格的顶点上已知。如果0≤ ≤ -->λ λ -->i≤ ≤ -->1∀ ∀ -->i∈ ∈ -->1,2,3{\displaystyle 0\leq \lambda _{i}\leq 1\;\forall \;i\in {1,2,3}}，则点p{\displaystyle {\textbf {p}}}位于三角形内部或边界上。我们取f{\displaystyle f}的插值为

这个线性插值是自动正规的因为λ λ -->1+λ λ -->2+λ λ -->3=1{\displaystyle \lambda _{1}+\lambda _{2}+\lambda _{3}=1}。

四面体的重心坐标

重心坐标容易推广到三维空间。3维单形即四面体，具有四个三角形面和四个顶点。

完全类似于三角形，四面体v1,v2,v3,v4{\displaystyle {\textbf {v}}_{1},{\textbf {v}}_{2},{\textbf {v}}_{3},{\textbf {v}}_{4}}的顶点v1{\displaystyle {\textbf {v}}_{1}}的重心坐标为（1,0,0,0），v2{\displaystyle {\textbf {v}}_{2}}为（0,1,0,0），如是等等。

点p{\displaystyle {\textbf {p}}}的笛卡尔坐标和为关于四面体v1,v2,v3,v4{\displaystyle {\textbf {v}}_{1},{\textbf {v}}_{2},{\textbf {v}}_{3},{\textbf {v}}_{4}}的重心坐标的关系：

这里Vol(V1V2V3V4){\displaystyle {\text{Vol}}(V_{1}V_{2}V_{3}V_{4})}为v1,v2,v3,v4{\displaystyle {\textbf {v}}_{1},{\textbf {v}}_{2},{\textbf {v}}_{3},{\textbf {v}}_{4}}组成的四面体的体积，类似于三角形也可以用笛卡尔坐标的一个行列式表示出来。

3维重心坐标和2维一样，可以确定一点是否位于四面体内部，也能对四面体网格上函数插值。因为利用重心坐标可以极大地简化3维插值，四面体网格经常用于有限元分析。

参考文献

Bradley, Christopher J. The Algebra of Geometry: Cartesian, Areal and Projective Co-ordinates. Bath: Highperception. 2007. ISBN 978-1-906338-00-8. 

MathWorld上Areal Coordinates的资料，作者：埃里克·韦斯坦因。

MathWorld上Barycentric Coordinates的资料，作者：埃里克·韦斯坦因。

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。