性质

面的图形：正五边形 面的数目：12 边的数目：30 顶点数目：20 二面角角度： θ θ --> = arccos ⁡ ⁡ --> ( − − --> 1 5 ) = 2 arctan ⁡ ⁡ --> φ φ --> ≈ ≈ --> 116.5650512 ∘ ∘ --> {\displaystyle {\boldsymbol {\theta }}=\arccos \left(-{\frac {1}{\sqrt {5}}}\right)=2\arctan \varphi \approx 116.5650512^{\circ }} 如果正十二面体棱长为a： 表面积： A = 3 25 + 10 5 a 2 ≈ ≈ --> 20.645728807 a 2 {\displaystyle A=3{\sqrt {25+10{\sqrt {5}}}}a^{2}\approx 20.645728807a^{2}} 体积： V = 1 4 ( 15 + 7 5 ) a 3 ≈ ≈ --> 7.6631189606 a 3 {\displaystyle V={\frac {1}{4}}(15+7{\sqrt {5}})a^{3}\approx 7.6631189606a^{3}} 外接球半径： r u = a 3 4 ( 1 + 5 ) ≈ ≈ --> 1.401258538 ⋅ ⋅ --> a {\displaystyle r_{u}=a{\frac {\sqrt {3}}{4}}\left(1+{\sqrt {5}}\right)\approx 1.401258538\cdot a} 内切球半径： r i = a 1 2 5 2 + 11 10 5 ≈ ≈ --> 1.113516364 ⋅ ⋅ --> a {\displaystyle r_{i}=a{\frac {1}{2}}{\sqrt {{\frac {5}{2}}+{\frac {11}{10}}{\sqrt {5}}}}\approx 1.113516364\cdot a} 中交球半径： r m = a 1 4 ( 3 + 5 ) ≈ ≈ --> 1.309016994 ⋅ ⋅ --> a {\displaystyle r_{m}=a{\frac {1}{4}}\left(3+{\sqrt {5}}\right)\approx 1.309016994\cdot a}

我们亦可以将上述三式写作：

注意到棱长为a的正十二面体的外接球同样外接于棱长为 φ a的立方体，并且其内切球半径（也即面心距）等于棱长为 φ a的正五边形的边心距。

对偶多面体：正二十面体

坐标系

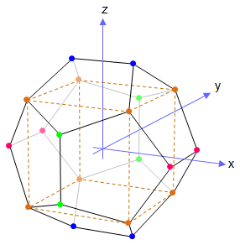
如果我们以正十二面体的形心为原点建立三维直角坐标系，那么其20个顶点可被描述为： (0,±φ,±1/φ) (±1/φ,0,±φ) (±φ,±1/φ,0) (±1,±1,±1) 其中φ = (1+√5)/2，是黄金分割数，也被写作τ，约等于1.618。 该正十二面体棱长为 / φ =√5–1。其内接球半径正好为√3。

二维投影和对称性

正十二面体有两种特殊的正交投影，分别正对着其一个顶点和一个正五边形面，对应着A 2 和H 2 考克斯特平面 （ 英语 ： Coxeter plane ）

在透视投影中，如果如果投影中心正在正十二面体外接球正对其一面的一点，则你能得到其 施莱格尔图像 （ 英语 ： schlegel diagram ） ，我们亦可以将其视为 球面多面体 （ 英语 ： Spherical polyhedron ） 而使用球极投影。这些方法也被用于可视化其四维类比正一百二十胞体，一个由120个全等的正十二面体组成的四维凸正多胞体。

几何关联

正十二面体是一个无穷家族——截顶偏方面体的第3个成员（截顶五偏方面体）。这类多面体可以被看作是将偏方面体在旋转对称轴上的两个相对的顶点截去而成。

正十二面体的 星形化体 （ 英语 ： Stellation ） 构成了4个星形正多面体中的3个。

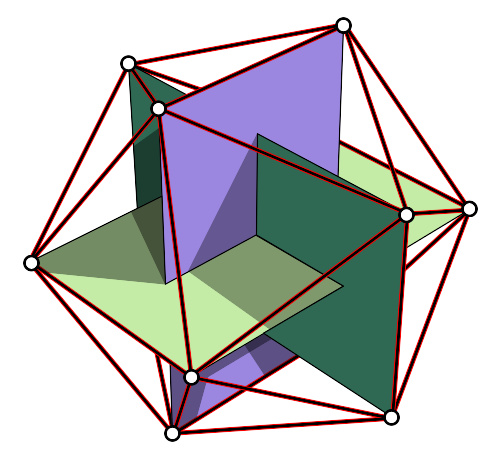
我们可以在正十二面体的20个顶点中选取5组这样的顶点，使任意两个顶点的连线都是正十二面体正五边形面的一条对角线，这样能构成正十二面体的内接立方体，5个内接立方体一起构成了——复合多面体——五复合立方体；我们还可以进一步对内接立方体做交错操作，得到正十二面体的内接正四面体，如果我们只在内接立方体中取一个正四面体，则5个正四面体构成了有手征性的复合多面体——五复合四面体；如果取两个，则10个正四面体构成了复合多面体——十复合四面体，这三个复合多面体都是正十二面体的 小面化体 （ 英语 ： faceting ） 。

正十二面体的完全对称群是 正二十面体对称群 （ 英语 ： Icosahedral symmetry ） I h ，考克斯特群[5,3]，群阶120，还有一个抽象群结构A 5×Z 2。

与其对偶——正二十面体的关系

当正十二面体和正二十面体内接于同一球时，尽管正二十面体有更多的面，但正十二面体占据球的体积（66.49%）要多于正二十面体占据的球的体积（60.54%），这一点与二维不同。

棱长相同为1的正十二面体的体积（7.663...）是正二十面体体积（2.181...）的三倍半多。

相关多面体

正十二面体在拓扑上与一系列三阶正镶嵌（顶点图为 n ）有关：

正十二面体在拓扑上还和其它阶的正五边形正镶嵌{5,n}(n≥3)有关：

正十二面体可以通过不同类型的截取操作来得到一系列不同的半正多面体及其对偶，正二十面体，构成了正二十面体家族：

顶点分布

正十二面体与4个 星形半正多面体 （ 英语 ： nonconvex uniform polyhedron ） 和上述3个复合半正多面体有同样的顶点分布：

星形化体

正十二面体的3个 星形化体 （ 英语 ： stellation ） 都是星形正多面体（开普勒-普索多面体）：

倒角多面体

相关数学问题

哈密顿路径的理论就是源自一个和正十二面体有关的问题：试求一条路径，沿正十二面体的棱经过它所有的顶点。

真实世界

因为一年有12个月，正十二面体正好用来制作月历。

Pariacoto virus的形状结构是正十二面体。

在英国到匈牙利，至到意大利东部等地，找到过百个形状接近十二面体、以铜或石头制造的空心物件。它们被称为Dodecaeder，用途不明。

五魔方（Megaminx）就是正十二面体制作出来的魔方。

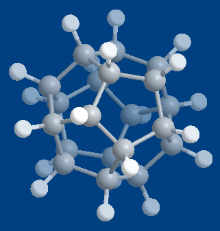
正十二面烷

化学：

硫化铁结晶体有时会出现接近正十二面体的形状。

最小的富勒烯C 20 结构如正十二面体。

正十二面体烷C 20 H 20 是个人工合成的碳氢化合物

参考文献

^12 sided calendarii.uib.no

^Roman Dodecahedrageorgehart.com

^Dodecaedermuseums.ncl.ac.uk

^Dodecahedrane—The chemical transliteration of Plato"s universepubmedcentral.nih.gov

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。