符号说明

余切最早用符号tan.com表示，该符号同正切一样，最初由T.芬克使用。后来人们又逐渐将该符号简化为ctg，后来又改为cot，与现代符号完全相同。

定义

直角三角形中

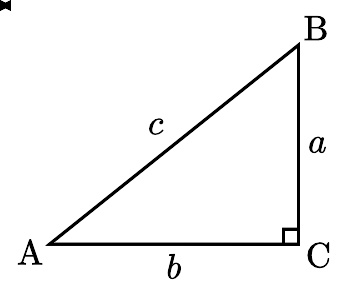
直角三角形，∠C为直角，∠A 的角度为 θ θ --> {\displaystyle \theta } ， 对于 ∠A 而言，a为对边、b为邻边、c为斜边

在直角三角形中，一个锐角的 余切 定义为它的邻边与对边的比值，也就是：

可以发现其定义和正切函数互为倒数。

直角坐标系中

设α是平面直角坐标系xOy中的一个象限角， P ( x , y ) {\displaystyle P\left({x,y}\right)} 是角的终边上一点， r = x 2 + y 2 > 0 {\displaystyle r={\sqrt {x^{2}+y^{2}}}>0} 是P到原点O的距离，则α的正切定义为：

单位圆定义

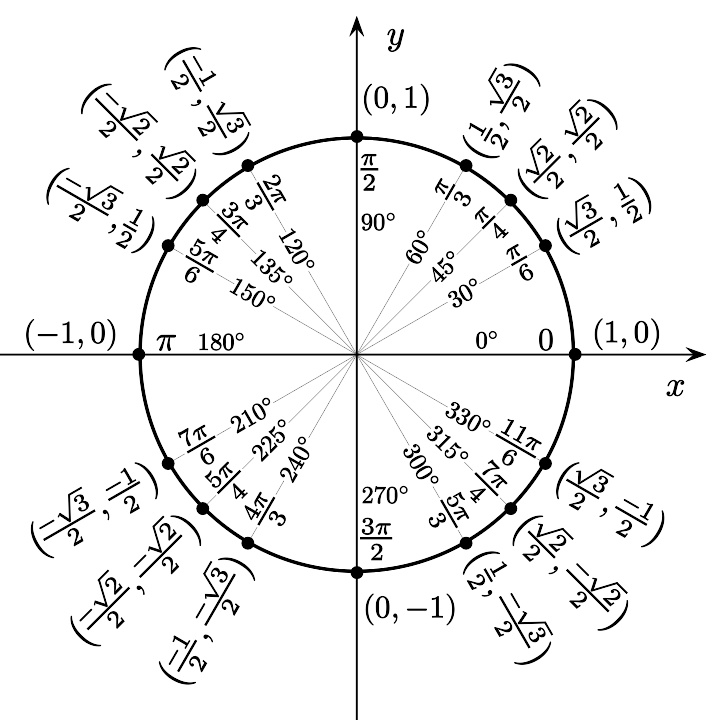
单位圆

图像中给出了用弧度度量的某个公共角。逆时针方向的度量是正角而顺时针的度量是负角。设一个过原点的线，同 x 轴正半部分得到一个角 θ，并与单位圆相交，并令这个交点为 y 。另原点为 O 。做一直线， y 点，垂直于 Oy ，并与单位圆相切，令直线与y轴的交点，则此点与 y 点之距离为余切比值。

单位圆上的余切

单位圆可以被认为是通过改变邻边和对边的长度，产生斜边等于 1 的无限数目个三角形的一种方式。

对于大于 2π 或小于 −2π 的角度，简单的继续绕单位圆旋转。在这种方式下，有些三角函数变成了周期为 2π的周期函数；但由于余切是切线，再绕单位圆旋转时，会出现周期是π，所以正切是周期为 π的周期函数:

对于任何角度 θ 和任何整数 k 。

级数定义

余切函数也可以使用泰勒展开式定义

微分方程定义

cot的微分是负csc的平方

另外

所以可以用

指数定义

cot ⁡ ⁡ --> θ θ --> = i ( e i θ θ --> + e − − --> i θ θ --> ) e i θ θ --> − − --> e − − --> i θ θ --> {\displaystyle \cot \theta ={\frac {{\mathrm {i} }(e^{{\mathrm {i} }\theta }+e^{-{\mathrm {i} }\theta })}{e^{{\mathrm {i} }\theta }-e^{-{\mathrm {i} }\theta }}}\,}

恒等式

用其它三角函数来表示余切

和差角公式

二倍角公式

cot ⁡ ⁡ --> 2 θ θ --> = cot 2 ⁡ ⁡ --> θ θ --> − − --> 1 2 cot ⁡ ⁡ --> θ θ --> = 1 cot ⁡ ⁡ --> θ θ --> − − --> 1 − − --> 1 cot ⁡ ⁡ --> θ θ --> + 1 {\displaystyle {\begin{aligned}\cot 2\theta &={\frac {\cot ^{2}\theta -1}{2\cot \theta }}\\&={\frac {1}{\cot \theta -1}}-{\frac {1}{\cot \theta +1}}\\\end{aligned}}}

半角公式

三倍角公式

余切定理

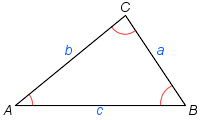
一个三角形。它的三个内角及其对边。

余切定理 是三角学中关于三角形内切圆半径的定理。

假设α, β, 与γ是三角形的三个内角， a , b , 与 c 是与之对应的三个对边，若

那么余切定理告诉我们：

还有

总而言之：余切定理就是某个角一半的余切等于半周长减去这个角所对的边长再除以三角形的内切圆半径。

参见

正弦

余弦

正切

正割

三角函数

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。