微分中值定理

微分中值定理分为罗尔中值定理、拉格朗日中值定理和柯西中值定理，又（统）称为微分学基本定理、有限改变量定理或有限增量定理，是微分学的基本定理之一，内容是说一段连续光滑曲线中必然有一点，它的斜率与整段曲线平均斜率相同（严格的数学表达参见下文）。

罗尔中值定理

罗尔定理的几何意义

如果函数f(x){\displaystyle f(x)}满足

在闭区间[a,b]{\displaystyle [a,b]}上连续；

在开区间(a,b){\displaystyle (a,b)}内可导；

在区间端点处的函数值相等，即f(a)=f(b){\displaystyle f(a)=f(b)}，

那么在(a,b){\displaystyle (a,b)}内至少有一点ξ ξ -->(a(ξ ξ -->)=0{\displaystyle f^{\prime }(\xi )=0}。这个定理称为罗尔定理。

拉格朗日中值定理及正式叙述

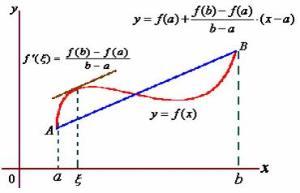
拉格朗日中值定理的几何意义

令f:[a,b]→ → -->R{\displaystyle f:[a,b]\rightarrow \mathbf {R} }为闭区间[a,b]{\displaystyle [a,b]}上连续函数续函数，且在开区间(a,b){\displaystyle (a,b)}内可导，其中a<b{\displaystyle a那么在(a,b){\displaystyle (a,b)}上存在某个c{\displaystyle c}使得

此定理称为拉格朗日中值定理。拉格朗日中值定理是罗尔中值定理的推广，同时也是柯西中值定理的特殊情形。

这个定理在一个更一般的条件下仍然成立。只需假设f:[a,b]→ → -->R{\displaystyle f:[a,b]\rightarrow \mathbf {R} }在[a,b]{\displaystyle [a,b]}连续，那么在(a,b){\displaystyle (a,b)}内对任意x{\displaystyle 极限，极限

存在，为一个有限数字或者等于+∞或−∞.如果有限，则极限等于f′(x){\displaystyle f"(x)}.（这里应该是f（x）的导数）定理的这个版本的应用的一个例子由从x{\displaystyle x}到x1/3{\displaystyle x^{1/3}}的实值三次方根函数映射给出，其导数在原点趋于无穷。

注意若一个可导函数是复变量的而不是实变量的，上面叙述的这个定理就不正确了。例如，对全部实数x{\displaystyle x}定义f(x)=eix{\displaystyle f(x)=e^{ix}}。那么

当|f′(x)|=1{\displaystyle |f"(x)|=1}时。

柯西中值定理

柯西中值定理，也叫拓展中值定理，是中值定理的一般形式。它叙述为：如果函数f和g都在闭区间[a,b]上连续，且在开区间(a, b)上可导，那么存在某个c ∈ (a,b),使得

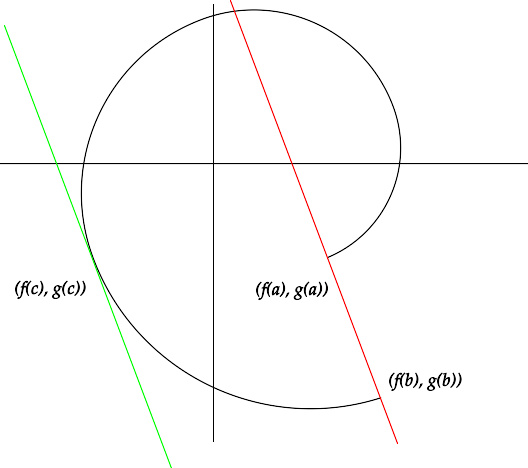
柯西定理的几何意义

当然，如果g(a) ≠ g(b)并且g′(c) ≠ 0,这等价于：

在几何上，这表示曲线

的图像存在平行于由(f(a),g(a))和(f(b),g(b))确定的直线的切线。但柯西定理不能表明在任何情况下不同的两点(f(a),g(a))和(f(b),g(b))都存在切线，因为可能存在一些c值使f′(c) = g′(c) = 0,换句话说取某个值时位于曲线的驻点;在这些点似乎曲线根本没有切线。下面是这种情形的一个例子

在区间[−1,1]上，曲线由(−1,0)到(1,0),却并无一个水平切线;然而它有一个驻点(实际上是一个尖点)在t = 0时。

柯西中值定理可以用来证明洛必达法则. (拉格朗日)中值定理是柯西中值定理当g(t) = t时的特殊情况。

积分中值定理

积分中值定理分为积分第一中值定理和积分第二中值定理，它们各包含两个公式。其退化状态均指在ξ的变化过程中存在一个时刻使两个图形的面积相等（严格表述在下面）。

积分第一中值定理

设f:[a,b]→ → -->R{\displaystyle f:[a,b]\rightarrow \mathbb {R} }为一连续函数，g:[a,b]→ → -->R{\displaystyle g:[a,b]\rightarrow \mathbb {R} }要求g(x)是可积函数且在积分区间不变号，那么存在一点ξ ξ -->∈ ∈ -->[a,b]{\displaystyle \xi \in [a,b]}使得

证明

在不失去一般性的条件下，设对所有x，g(x)≥0； 因为f{\displaystyle f}是闭区间上的连续函数，f{\displaystyle f}取得最大值M{\displaystyle M}和最小值m{\displaystyle m}。于是

若不等于零那么∫ ∫ -->abg(x)dx>0{\displaystyle \int _{a}^{b}g(x)\,dx>0}，

g(x)<0的情况按同样方法证明。

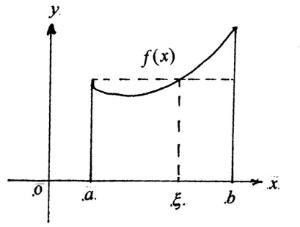
积分第一中值定理推论的几何意义

推论（拉格朗日中值定理的积分形式）

在上式中令g(x)=1{\displaystyle g(x)=1}，则可得出：

设f:[a,b]→ → -->R{\displaystyle f:[a,b]\rightarrow \mathbf {R} }为一连续函数，则∃ξ ξ -->∈ ∈ -->[a,b]{\displaystyle \xi \in [a,b]}，使

它也可以由拉格朗日中值定理推出：

设F(x){\displaystyle F(x)}在[a,b]{\displaystyle [a,b]}上可导，f(x)=F′ ′ -->(x){\displaystyle f(x)=F^{\prime }(x)}，则∃ξ ξ -->∈ ∈ -->[a,b]{\displaystyle \xi \in [a,b]}，使

积分第二中值定理

积分第二中值定理与积分第一中值定理相互独立，却又是更精细的积分中值定理。它可以用来证明Dirichlet-Abel反常Rieman积分判别法。

内容

若f,g在[a,b]上黎曼可积且f(x)在[a,b]上单调，则存在[a,b]上的点ξ使

退化态的几何意义

第二积分中值定理退化形式的几何意义

令g(x)=1，则原公式可化为：

进而导出：

此时易得其几何意义为： 能找到ξ∈[a,b]，使得S[红]+S[蓝]=S[阴影]，即S[I]=S[II]

参见

罗尔定理

柯西中值定理

介值定理

极值定理

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。