仿射曲线

定义在域F{\displaystyle F}上的仿射代数曲线可以看作是Fn{\displaystyle F^{n}}中由若干个n{\displaystyle n}-元多项式gi∈ ∈ -->F[x1,… … -->,xn]{\displaystyle g_{i}\in F[x_{1},\ldots ,x_{n}]}定义的公共零点，使得其维数为一。

利用结式，我们可以将变数消至两个，并化约到与之双有理等价的平面代数曲线f(x,y)=0{\displaystyle f(x,y)=0}，其中f∈ ∈ -->F[x,y]{\displaystyle f\in F[x,y]}，因此在探讨曲线的双有理几何时仅须考虑平面曲线。

射影曲线

射影空间中的曲线可视作仿射曲线的紧化，它们带有更好的几何性质。在以上考虑的方程gi=0{\displaystyle g_{i}=0}（i=1,… … -->,n− − -->1{\displaystyle i=1,\ldots ,n-1}）中，我们作代换：

遂得到n− − -->1{\displaystyle n-1}个齐次多项式，它们在射影空间PFn{\displaystyle \mathbb {P} _{F}^{n}}中定义一条曲线，此射影曲线与开集U0:={(X0:⋯ ⋯ -->:Xn)|X0≠ ≠ -->0}{\displaystyle U_{0}:=\{(X_{0}:\cdots :X_{n})|X_{0}\neq 0\}}的交集同构于原曲线。射影曲线的例子包括PQ3{\displaystyle \mathbb {P} _{\mathbb {Q} }^{3}}中的费马曲线Xn+Yn+Zn=0{\displaystyle X^{n}+Y^{n}+Z^{n}=0}，其上的有理点对应到费马方程Xn+Yn=Zn{\displaystyle X^{n}+Y^{n}=Z^{n}}的互素整数解。

代数函数域

更多资料：函数域

代数曲线之研究可化约为不可约代数曲线之研究，后者的范畴在双有理等价之意义下等价于代数函数域范畴。域F{\displaystyle F}上的函数域K{\displaystyle K}是超越次数为一的有限型域扩张，换言之：存在元素x∈ ∈ -->K{\displaystyle x\in K}使得x{\displaystyle x}在F{\displaystyle F}上超越，而且K/F(x){\displaystyle K/F(x)}是有限扩张。

以复数域C{\displaystyle \mathbb {C} }为例，我们可以定义复系数有理函数域C(x){\displaystyle \mathbb {C} (x)}。变元x,y{\displaystyle x,y}对代数关系y2=x3− − -->x− − -->1{\displaystyle y^{2}=x^{3}-x-1}生成的域C(x,y){\displaystyle \mathbb {C} (x,y)}是一个椭圆函数域，代数曲线{(x,y)∈ ∈ -->C2:y2=x3− − -->x− − -->1}{\displaystyle \{(x,y)\in \mathbb {C} ^{2}:y^{2}=x^{3}-x-1\}} 给出它的一个几何模型。

若基域F{\displaystyle F}非代数封闭域，则函数域无法只由多项式的零点描述，因为此时存在无点的曲线。例如可取实数域F:=R{\displaystyle F:=\mathbb {R} }并考虑其上的代数曲线x2+y2+1=0{\displaystyle x^{2}+y^{2}+1=0}，此方程定义了一个R[x]{\displaystyle \mathbb {R} [x]}的有限扩张，因而定义了一个函数域，然而

代数封闭域上的代数曲线可以用代数簇完整地描述，对于一般的基域或者环上的曲线论，概形论能提供较合适的框架。

复代数曲线与黎曼曲面

更多资料：黎曼曲面

复射影曲线可以嵌入n{\displaystyle n}维复射影空间CPn{\displaystyle \mathbb {C} P^{n}}。复射影曲线在拓扑上为二维的对象，当曲线光滑时，它是个紧黎曼曲面，即一维的紧复流形，因而是可定向的二维紧流形。这时该曲面的拓扑亏格（直观说就是曲面有几个洞或把手）等同于曲线上由代数几何学定义的亏格。视这类曲线为黎曼曲面，则可以采复分析手法加以研究。另一方面，黎曼则证明了任何紧黎曼曲面都同构于一条复射影曲线。

于是我们有三个相互等价的范畴：复数域上的不可约平滑射影曲线、紧黎曼曲面与C{\displaystyle \mathbb {C} }上的函数域。因此一维复分析（包括位势论）、代数几何与域论的方法此时能相互为用，这是高等数学里很常见的现象。

奇点

判断方式

曲线在一点P{\displaystyle P}的平滑性可以用雅可比矩阵判断。以下考虑嵌于Pn{\displaystyle \mathbb {P} ^{n}}中的曲线：设该曲线由n− − -->1{\displaystyle n-1}个n+1{\displaystyle n+1}个变元的齐次多项式g1,… … -->,gn− − -->1{\displaystyle g_{1},\ldots ,g_{n-1}}定义，若其雅可比矩阵(∂ ∂ -->gi∂ ∂ -->xj)i,j{\displaystyle \left({\frac {\partial g_{i}}{\partial x_{j}}}\right)_{i,j}}在区线上一点P{\displaystyle P}满秩，则称它P{\displaystyle P}点光滑；反之则称为奇点。在一点的平滑性与多项式g1,… … -->,gn− − -->1{\displaystyle g_{1},\ldots ,g_{n-1}}的选取无关，也与曲线的嵌入方式无关。

在平面射影曲线的例子，假设曲线C{\displaystyle C}由齐次方程式f(x,y,z)=0{\displaystyle f(x,y,z)=0}定义，则C{\displaystyle C}的奇点恰为C{\displaystyle C}上使得∇ ∇ -->f{\displaystyle \nabla f}为零的点，即：

在特征非零的域上，一条代数曲线仅有有限个奇点；无奇点的曲线即平滑曲线。奇点在双有理映射下可能映为光滑点；事实上，奇点总是可借着平面的拉开映射或正规化解消，由此得到的新平滑曲线仍双有理等价于原曲线；然而对代数封闭域上的射影曲线，其奇点总数则关系到曲线的几何亏格，后者是个双有理不变量。

奇点分类

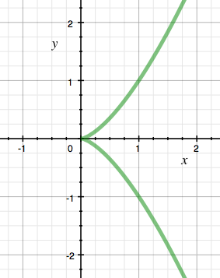
x = y

曲线的奇点包括多重点（这是曲线的自交点）及尖点（如仿射曲线x3=y2{\displaystyle x^{3}=y^{2}}之于原点(0,0){\displaystyle (0,0)}，见右图）等等。一般来说，仿射平面曲线f(x,y)=0{\displaystyle f(x,y)=0}在一点P{\displaystyle P}的奇点性质可以透过下述方式理解：

透过平移，不妨假设P=(0,0){\displaystyle P=(0,0)}。将多项式f(x,y){\displaystyle f(x,y)}写成

其中fn(x,y){\displaystyle f_{n}(x,y)}是n{\displaystyle n}次齐次多项式。直观地想像，f(x,y)=0{\displaystyle f(x,y)=0}在原点附近的性状仅决定于最低次的非零项，设之为fm(x,y){\displaystyle f_{m}(x,y)}。根据齐次性可以将之分解成

换言之，曲线在原点附近将近似于m{\displaystyle m}条（含重复）直线aix− − -->biy=0{\displaystyle a_{i}x-b_{i}y=0}的联集。上式中相异的直线数r{\displaystyle r}称作分支数，正整数m{\displaystyle m}称作平面曲线在该点的重数，此外还有一个内在的不变量δ δ -->P:=dim⁡ ⁡ -->OC~ ~ -->,P/OC,P{\displaystyle \delta _{P}:=\dim {\mathcal {O}}_{{\tilde {C}},P}/{\mathcal {O}}_{C,P}}，其中C~ ~ -->→ → -->C{\displaystyle {\tilde {C}}\rightarrow C}是该曲线的正规化态射。资料[m, δ, r]能够被用来分类奇点。例如一般尖点对应到[2,1,1]{\displaystyle [2,1,1]}，一般双重点对应到[2,1,2]{\displaystyle [2,1,2]}，而一般n重点则对应到[n,n(n− − -->1)2,n]{\displaystyle [n,{\frac {n(n-1)}{2}},n]}。

各奇点的不变量δP决定平面曲线f(x,y)=0{\displaystyle f(x,y)=0}的亏格：设deg⁡ ⁡ -->f=d{\displaystyle \deg f=d}，则有

对于在复数域上的平面曲线，John Milnor以拓扑方式定义了不变量μ，称为Milnor数：同样假设P=(0,0){\displaystyle P=(0,0)}，在原点附近够小的四维球Bϵ ϵ -->:={(x,y)∈ ∈ -->C2:|x|2+|y|2}{\displaystyle B_{\epsilon }:=\{(x,y)\in \mathbb {C} ^{2}:|x|^{2}+|y|^{2} 内有(x,y)≠ ≠ -->(0,0)⇒ ⇒ -->∇ ∇ -->f(x,y)≠ ≠ -->0{\displaystyle (x,y)\neq (0,0)\Rightarrow \nabla f(x,y)\neq 0}，此时有连续映射

由于Bϵ ϵ -->− − -->{(0,0)}{\displaystyle B_{\epsilon }-\{(0,0)\}}同伦等价于三维球面S3{\displaystyle \mathbb {S} ^{3}}，于是可定义μ为此映射的拓扑次数。μ与前述不变量的关系由下式表明：

事实上，{(x,y)∈ ∈ -->C2:f(x,y)=0}∩ ∩ -->{(x,y)∈ ∈ -->C2:|x|2+|y|2=ϵ ϵ -->}{\displaystyle \{(x,y)\in \mathbb {C} ^{2}:f(x,y)=0\}\cap \{(x,y)\in \mathbb {C} ^{2}:|x|^{2}+|y|^{2}=\epsilon \}}在ε够小时是{(x,y)∈ ∈ -->C2:|x|2+|y|2=ϵ ϵ -->}≅ ≅ -->S3{\displaystyle \{(x,y)\in \mathbb {C} ^{2}:|x|^{2}+|y|^{2}=\epsilon \}\cong \mathbb {S} ^{3}}中的一个环圈，称作奇点环圈，它具有复杂的拓扑性质。例如：x3=y2{\displaystyle x^{3}=y^{2}}在尖点附近的奇点环圈是三叶结。

曲线的例子

有理曲线

域F{\displaystyle F}上的有理曲线是双有理等价于射影直线PF1{\displaystyle \mathbb {P} _{F}^{1}}的曲线，换言之，其函数域同构于单变元有理函数域F(t){\displaystyle F(t)}。当F{\displaystyle F}代数封闭时，这也等价于该曲线之亏格为零，对一般的域则不然；实数域上由x2+y2+1=0{\displaystyle x^{2}+y^{2}+1=0}给出的函数域亏格为零，而非有理函数域。

具体地说，一条有理曲线是能以有理函数参数化的曲线，例子请见条目有理正规曲线。

任何F{\displaystyle F}上有有理点的圆锥曲线都是有理曲线。参数化的过程如下：过给定有理点P{\displaystyle P}而斜率为t{\displaystyle t}的直线交平面上一条二次曲线于两点，就x坐标来说，交点的x坐标是一个二次多项式的根，其中一个属于F{\displaystyle F}的根已知，即P{\displaystyle P}的x坐标；因此透过根与系数的关系得知另一根也属于F{\displaystyle F}，而且能表作t{\displaystyle t}在F{\displaystyle F}上的有理函数。y坐标的作法相同。

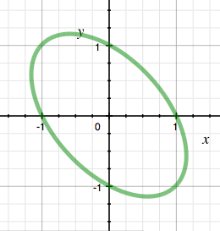
x + xy + y = 1

例。考虑斜椭圆E:x2+xy+y2=1{\displaystyle E:x^{2}+xy+y^{2}=1}，其中(− − -->1,0){\displaystyle (-1,0)}是有理点。画一条过该点且斜率为t之直线y=t(x+1){\displaystyle y=t(x+1)}，并带入E的等式，于是得到：

这就给出E的有理参数化，于是证明了E是有理曲线。

将此结果置于射影几何的框架下，则能导出若干数论的结论。例如我们可在E中加入无穷远点，得到射影曲线

以上参数化遂表为

若取t{\displaystyle t}为整数，对应的X,Y,Z{\displaystyle X,Y,Z}是不定方程X2+XY+Y2=Z2{\displaystyle X^{2}+XY+Y^{2}=Z^{2}}的整数解；若将X{\displaystyle X}代以− − -->X{\displaystyle -X}，则此方程诠释为θ=60余弦定理弦定理，借此能描述所有一角为 60°且边长均为整数的三角形，例如取t=2{\displaystyle t=2}，就得到边长分别为X=3, Y=8, Z=7的三角形。

椭圆曲线

更多资料：椭圆曲线

椭圆曲线可以定义为任意亏格等于一且给定一个有理点的代数曲线，它们都同构于平面上的三次曲线。此时通常取无穷远处的反曲点为给定的有理点，这时该曲线可以写作射影版本的Tate-魏尔施特拉斯形式：

椭圆曲线带有唯一的阿贝尔群结构，使得给定有理点为单位元素，且加法为代数簇的态射，因而椭圆曲线构成一个阿贝尔簇。在三次平面曲线的情形，三点和为零当且仅当它们共线。对于复数域上的椭圆曲线，此阿贝尔簇同构于C/Λ Λ -->{\displaystyle \mathbb {C} /\Lambda }，其中的Λ Λ -->{\displaystyle \Lambda }由相应的椭圆函数给出。

亏格大于一的曲线

对亏格大于一的曲线，其性质与有理曲线与椭圆曲线有显著不同。根据Faltings定理，定义在数域上的这类曲线只有有限个有理点；若视为黎曼曲面，它们则带有双曲几何的结构。例子包括超椭圆曲线、克莱因四次曲线与一开始提到的费马曲线在n≥ ≥ -->4{\displaystyle n\geq 4}的情形。

文献

Egbert Brieskorn and Horst Knörrer, Plane Algebraic Curves, John Stillwell, trans., Birkhäuser, 1986

Claude Chevalley, Introduction to the Theory of Algebraic Functions of One Variable, American Mathematical Society, Mathematical Surveys Number VI, 1951

Hershel M. Farkas and Irwin Kra, Riemann Surfaces, Springer, 1980

Phillip A. Griffiths, Introduction to Algebraic Curves, Kuniko Weltin, trans., American Mathematical Society, Translation of Mathematical Monographs volume 70, 1985 revision

Robin Hartshorne, Algebraic Geometry, Springer, 1977

Shigeru Iitaka, Algebraic Geometry: An Introduction to the Birational Geometry of Algebraic Varieties, Springer, 1982

John Milnor, Singular Points of Complex Hypersurfaces, Princeton University Press, 1968

George Salmon, Higher Plane Curves, Third Edition, G. E. Stechert & Co., 1934

Jean-Pierre Serre, Algebraic Groups and Class Fields, Springer, 1988

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。