简述

同调代数是一门相对年轻的学科，其源头可追溯到代数拓扑（单纯形同调）与抽象代数（合冲模）在十九世纪末的发展，这两门理论各自由庞加莱与希尔伯特开创。

同调代数的发展与范畴论的出现密不可分。大致说来，同调代数是（上）同调函子及其代数结构的研究。“同调”与“上同调”是一对对偶的概念，它们满足的范畴论性质相反（即：箭头反向）。数学很大一部分的内在构造可藉链复形理解，其性质则以同调与上同调的面貌展现，同调代数能萃取这些链复形蕴含的资讯，并表之为拓扑空间、层、群、环、李代数与C*-代数等等“具体”对象的（上）同调不变量。谱序列是计算这些量的有力工具。

同调代数肇始即在代数拓扑中扮演要角。其影响日渐扩大，目前已遍及交换代数、代数几何、代数数论、表示理论、算子代数、偏微分方程与非交换几何。K-理论是一门独立的学科，它也采用同调代数的办法。

主要对象：链复形

同调代数领域的基本对象是一个链复形 ( A ∙ ∙ --> , d ∙ ∙ --> ) {\displaystyle (A_{\bullet },d_{\bullet })} 。这是一个由交换群、模或更广义地说是由一个阿贝尔范畴的对象组成的序列A0, A1, A2……。它同态过一系列同态dn : An→An-1相连，使得每两个连接的映射的合成 为零：对所有n有dn o dn+1 = 0（有时迳写作 d 2 = 0 {\displaystyle d^{2}=0} ）

链复形的同调群定义为：

同调群皆为零的链复形称作正合的。

两个链复形 ( A ∙ ∙ --> , d A , ∙ ∙ --> ) {\displaystyle (A_{\bullet },d_{A,\bullet })} 、 ( B ∙ ∙ --> , d B , ∙ ∙ --> ) {\displaystyle (B_{\bullet },d_{B,\bullet })} 之间的链映射是一族同态 f n : A n → → --> B n {\displaystyle f_{n}:A_{n}\rightarrow B_{n}} ，使之满足： f n ∘ ∘ --> d A , n = d B , n ∘ ∘ --> f n + 1 {\displaystyle f_{n}\circ d_{A,n}=d_{B,n}\circ范畴_{n+1}} ；全体链复形依此构成一范畴。链映射诱导出同调群的映射。

对链映射可以定义同伦的概念，这是拓扑学的同伦在代数框架下的翻译。同伦的链映射在同调群上诱导出相同的映射。

在同调群上诱导出同构的链映射称作拟同构。

链复形概念的一个对偶版本是上链复形。一个上链复形 ( A ∙ ∙ --> , d ∙ ∙ --> ) {\displaystyle (A^{\bullet },d^{\bullet })} 是个序列A, A, A……。它们由一系列同态d : A→A相连，使得任何两个接连的映射的合成为零：对所有n有d o d = 0：

关于链复形的种种定义可以照搬至上链复形；实质上，我们仅须将原定义中的所有箭头反转。例如上链复形的上同调群定义为：

形式地说，同调代数可定义为链复形与上链复形的抽象研究。以下我们将看到它的具体根源。

溯源

代数拓扑学的黎明

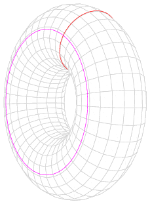
  环面上的两种闭曲线，它们都无法表成区域的边界。

同调代数的根源之一在代数拓扑，而后者的历史则可上溯至十九世纪中。早在黎曼关于阿贝尔簇的工作中，就已考虑过黎曼曲面上的闭曲线是否为一块区域的边界的问题；根据斯托克斯定理，闭形式在这类闭曲线上的积分恒为零，而这类曲线的多寡显然牵涉到曲面的拓扑性状。黎曼依此定义了“连通数”——用现代的语言表述即是 1 + dim ⁡ ⁡ --> H 1 ( X ; Z / 2 Z ) {\displaystyle 1+\dim H_{1}(X;\mathbb {Z} /2\mathbb {Z} )} ，此量关系到黎曼曲面的亏格，直观地理解便是曲面上有几个“洞”。

庞加莱在1895年的经典论文Analysis Situs及其后续工作真正奠定了代数拓扑学的基础。他考虑的对象是后来所谓的单纯复形，这类空间在同胚的意义下可剖分为多面体，它包含了微分拓扑中处理的大多数有限维空间。庞加莱考虑一个单纯复形 X {\displaystyle X} 中各种维度的单纯形（零维的点、一维的线、二维的三角形、三维的四面体等等）的整系数线性组合，称之为链，它们构成一系列的阿贝尔群 C 0 ( X ) , C 1 ( X ) , C 2 ( X ) , … … --> {\displaystyle C_{0}(X),C_{1}(X),C_{2}(X),\ldots } ，其中下标代表维度。庞加莱还定义了一个边界映射 ∂ ∂ --> i : C i ( X ) → → --> C i − − --> 1 ( X ) {\displaystyle \partial _{i}:C_{i}(X)\rightarrow C_{i-1}(X)} ，它在单纯形上的作用是将 i {\displaystyle i} 维单纯形的 ( i − − --> 1 ) {\displaystyle (i-1)} 维边界取适当正负号后作线性组合；彼此差个边界的链在拓扑上称作同调的，这也是同调代数的词源。庞加莱证明 ∂ ∂ --> i − − --> 1 ∘ ∘ --> ∂ ∂ --> i = 0 {\displaystyle \partial _{i-1}\circ \partial _{i}=0} ，于是我们有以下链复形

定义 X {\displaystyle X} 的贝蒂数与欧拉示性数：

b i ( X ) := dim ⁡ ⁡ --> K e r ( ∂ ∂ --> i ) I m ∂ ∂ --> i + 1 ⊗ ⊗ --> Q {\displaystyle b_{i}(X):=\dim {\dfrac {\mathrm {Ker} (\partial _{i})}{\mathrm {Im} \partial _{i+1}}}\otimes \mathbb {Q} }

χ χ --> ( X ) := ∑ ∑ --> i ( − − --> 1 ) i b i = ∑ ∑ --> i ( − − --> 1 ) i dim ⁡ ⁡ --> C i ( X ) ⊗ ⊗ --> Q {\displaystyle \chi (X):=\sum _{i}(-1)^{i}b_{i}=\sum _{i}(-1)^{i}\dim C_{i}(X)\otimes \mathbb {Q} }

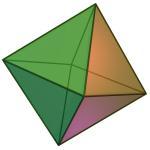
  单纯复形的例子：八面体，它有6个顶点、12个边和8个面

这两个量都与空间 X {\displaystyle X} 的剖分方式无关，仅决定于空间的伦型。起初庞加莱只考虑数值不变量；在1925年，埃米·诺特于一份只有14行的报告中指出：根本的不变量是阿贝尔群 H i ( X ) = K e r ( ∂ ∂ --> i ) / I m ∂ ∂ --> i + 1 {\displaystyle H^{i}(X)=\mathrm {Ker} (\partial _{i})/\mathrm {Im} \partial _{i+1}} ，而不仅仅是它派生的非负整数 b i = dim ⁡ ⁡ --> H i ( X ) ⊗ ⊗ --> Q {\displaystyle b_{i}=\dim H^{i}(X)\otimes \mathbb {Q} } ；群结构能给出更细的拓扑资讯，而空间的连续映射能导出同调群的同态。代数拓扑的风貌从此遂彻底改变。

循此脉络，L. Mayer在1929年定义了抽象的链复形及其同调群。同调理论自此有了纯代数的框架。

随后十年间，数学家们为各种空间定义了形形色色的同调与上同调，例如在德拉姆上同调中，我们设 Ω Ω --> i ( M ) {\displaystyle \Omega ^{i}(M)} 为光滑流形 M {\displaystyle M} 上的 i {\displaystyle i} 次微分形式，同态 d i : Ω Ω --> i ( M ) → → --> Ω Ω --> i + 1 ( M ) {\displaystyle d^{i}:\Omega ^{i}(M)\rightarrow \Omega ^{i+1}(M)} 定义为外微分。无论哪种理论，对同一空塞缪尔·艾伦伯格同诺曼·斯廷罗德艾伦伯格与诺曼·斯廷罗德在1945年以公理化方法梳理拓扑空间的（上）同调理论，从而证明先前种种理论只是同一个对象的不同面貌。此时同调代数俨然已自成一格了。

此后拓扑学仍不断为同调代数注入动力，例子包括了：

万有系数定理：关系到函子 T o r 1 ( − − --> , − − --> ) {\displaystyle \mathrm {Tor} _{1}(-,-)} 与 E x t 1 ( − − --> , − − --> ) {\displaystyle \mathrm {Ext} ^{1}(-,-)} 。这个定理告诉我们如何从系数为 Z {\displaystyle \mathbb {Z} } 的（上）同调群决定任意系数的情形。

非球空间的上同调群：它们可由基本群的群上同调算出，这也是一种Ext函子。

李群的上同调群：由其李代数决定，由此催生了李代数上同调理论。

希尔伯特与合冲模

同调代数的另一条线索可以追溯到十九世纪的显学不变量理论与大卫·希尔伯特。希尔伯特为了研究不变量本身、不变量间的关系、以及关系间的关系……，而考虑自由分解的问题：设 A {\displaystyle A} 为诺特环， M {\displaystyle M} 为有限生成的 A {\displaystyle A} -模，

希尔伯特基底定理（1888年）。存在正整数 n 0 {\displaystyle n_{0}} 及满态射 ϕ ϕ --> 0 : A n 0 → → --> M {\displaystyle \phi _{0}:A^{n_{0}}\rightarrow M} 。

设 M 1 := K e r ( ϕ ϕ --> 0 ) {\displaystyle M_{1}:=\mathrm {Ker} (\phi _{0})} ，则 0 ⟶ ⟶ --> M 1 ⟶ ⟶ --> A n 0 ⟶ ⟶ --> ϕ ϕ --> 0 M ⟶ ⟶ --> 0 {\displaystyle 0\longrightarrow M_{1}\longrightarrow A^{n_{0}}{\stackrel {\phi _{0}}{\longrightarrow }}M\longrightarrow 0} 是 M {\displaystyle M} 的一个有限展示； M 1 {\displaystyle M_{1}} 称作第一个合冲模（syzygy）。

另一方面， M 1 {\displaystyle M_{1}} 也是有限生成的，于是存在另一个有限展示

M 2 {\displaystyle M_{2}} 称作第二个合冲模。反复操作遂得到一个 A {\displaystyle A} -模的链复形：

其中每个同态的核都是前一个同态的像；用现代语言来说，这乃是 M {\displaystyle M} 的一个自由分解，长度最短的自由分解称作极小分解。自由分解的好处在于：自由模的不变量很容易计算，而透过自由分解又能适当地拼合各个 A n i {\displaystyle A^{n_{i}}} 上的资讯，从而推出 M {\displaystyle M} 的代数性质。这是同调代数的基本技术之一。

希尔伯特合冲定理（1890年）。上述分解在有限步之内停止；换言之，存在够大的 N {\displaystyle N} 使得第 N {\displaystyle N} 个合冲模 M N {\displaystyle M_{N}} 是自由模。当 k {\displaystyle k} 是域而 A := k [ X 1 , … … --> , X n ] {\displaystyle A:=k[X_{1},\ldots ,X_{n}]} 时，极小分解的长度不大于 n {\displaystyle n} 。

希尔伯特借着一个分次版的合冲定理证明了：在同样条件下，一个有限生成分次模的希尔伯特函数是个多项式；他借此阐明了不变量的个数对次数的关系。希尔伯特考虑的自由分解是投射分解的特例；在现代的同调代数理论中，投射分解及内射分解是定义导函子的基础。

当 A {\displaystyle A} 是局部环时，极小分解的长度称作 M {\displaystyle M} 的投射维度，它相当于使下式成立的最小整数 n {\displaystyle n} ：

对所有 A {\displaystyle A} -模的投射维度取极大值，得到的数称为同调维度；同调维度等于 dim ⁡ ⁡ --> A {\displaystyle \dim A} 当且仅当 A {\displaystyle A} 是正则局部环；在这个意义下，可以说极小分解反映了几何性质。合冲模也是计算代数几何中的重要方法。

嘉当-艾伦伯格革命

昂利·嘉当与塞缪尔·艾伦伯格在1956年出版的著作Homological Algebra标示了同调代数的成熟。书中的概念与工具影响之深广，成为各领域数学家们不可须臾离的生活资料。以下举出数点例子：

投射模与内射模

左正合函子与右正合函子

投射分解与内射分解，并由此定义一个函子的导函子。

将Tor函子与Ext函子分别定义为 M ⊗ ⊗ --> R − − --> {\displaystyle M\otimes _{R}-} 与 H o m R ( − − --> , M ) {\displaystyle \mathrm {Hom} _{R}(-,M)} 的右导函子与左导函子，并探讨了同调维度。

介绍了谱序列，并用以计算Tor与Ext。

链复形的嘉当-艾伦伯格分解与超上同调，可视为导范畴的滥觞。

一直到1970年代，嘉当与艾伦伯格的著作都是同调代数的圣经，同时期受欢迎的教本还有麦克兰恩的Homology，格罗滕迪克的《代数几何基础》与东北论文。

嘉当在1980年接受牛津大学荣誉博士时，曾用拉丁文写下这么一段话：

格罗滕迪克的东北论文

更多资料：阿贝尔范畴

亚历山大·格罗滕迪克在1955年左右对韦伊猜想发生兴趣，而真正勾动他的是此猜想的上同调表述；格罗滕迪克为此开始研习同调代数，当时嘉当-艾伦伯格的书尚未出版。嘉当与艾伦伯格仅考虑模构成的范畴。格罗滕迪克在1956年一封给塞尔的信中写道：

这封信铺陈了后来所谓东北论文的梗概。空间的上同调系指层上同调，当时是以Čech上同调或细层分解定义的；而所谓细层是一类带有单位分解的层，因此只在仿紧空间（当时称作可分空间）上有细层分解；这对微分几何与复几何不成问题，但对一般的代数簇则是致命缺陷。塞尔回复道：

格罗滕迪克遂着手重写同调代数的基础。

这条思路在他于1957年发表于《东北数学杂志》的论文Sur quelques points d"algèbre homologique中开花结果。原本区区数页的简单定义变为102页的范畴论论证，谣传他因此花了两年才找到地方刊登；但后续发展证明他的努力与收获是相称的。论文提出的重要观念如下：

阿贝尔范畴的公理

δ-函子与泛δ-函子

相对于一个函子的非循环对象：例如仿紧空间上的细层之于截面函子。

格罗滕迪克谱序列：涉及如何计算合成函子的导函子，可从此导出嘉当-艾伦伯格书中的许多谱序列与拓扑学中的Leray谱序列。

格罗滕迪克借此将层上同调化为导函子的特例，阿贝尔范畴也成为同调代数的标准语言。

导范畴

更多资料：导范畴

  八角形公理图解，它是三角范畴最难理解的公理之一。

格罗滕迪克在1961年左右面临一个技术瓶颈：为了为任意概形上的凝聚层建立对偶定理，必须为同调代数发展新工具。这个任务由他的学生让-路易·韦迪耶（Jean-Louis Verdier）完成了。

Verdier在1967年的博士论文Des Catégories Dérivées des Catégories Abéliennes中引入了三角范畴与导范畴的观念。约略地说，三角范畴是一种能制造长正合序列与上同调函子的范畴；一个阿贝尔范畴 A {\displaystyle {\mathcal {A}}} 上的链复形范畴 C ( A ) {\displaystyle C({\mathcal {A}})} 便是一例。其次，我们等同 C ( A ) {\displaystyle C({\mathcal {A}})} 中同伦等价的态射，从而得到商范畴 K ( A ) {\displaystyle K({\mathcal {A}})} ，它仍然具备三角范畴的结构；最后，建构 K ( A ) {\displaystyle K({\mathcal {A}})} 对拟同构的局部化以获得导范畴 D ( A ) {\displaystyle D({\mathcal {A}})} ，换言之即是为所有拟同构添加逆态射。

假设 A {\displaystyle {\mathcal {A}}} 有够多内射元，则在导范畴里同样可以定义左正合函子 F {\displaystyle F} 的右导函子 R F ( − − --> ) {\displaystyle RF(-)} ，它与古典定义 R n F ( − − --> ) {\displaystyle R^{n}F(-)} 的关系由下式给出：

假设左正合函子 G {\displaystyle G} 将内射对象映至 F {\displaystyle F} 的非循环对象，此时格罗滕迪克谱序列化作格外简明的形式：

对右正合函子也有相应的结果。尽管谱序列在导范畴的进路中不是那么根本，但在具体计算时仍占一席之地。

Verdier藉这套语言证明了Verdier对偶定理，这是庞加莱对偶定理的深远推广，适用于任何局部紧有限维拓扑空间。导范畴的应用仍在不断扩大中；在代数几何之外，导范畴理论的最大成功之一是证明了任意维度的黎曼-希尔伯特对应。

Verdier直到1996年才出版他的博士论文，此前导范畴的第一手资料是由他执笔的SGA4½末章：Catégories dérivées (état 0)。

单纯形法

庞加莱研究拓扑的方法是将空间剖分为多面体，这时空间的拓扑性质完全决定于这些点、线、面……等等[“单纯形”及其间的相交关系。将这套方法抽象化，便可对任何范畴 A {\displaystyle {\mathcal {A}}} 定义单纯形对象（及其对偶上单纯形对象）。在 A {\displaystyle {\mathcal {A}}} 为集合范畴的情形特别有用，此时的单纯形对象称为单纯形集合（及其对偶上单纯形集合）。对单纯形集合可定义其几何实现，这是一个CW-复形。对于来自一个源自拓扑空间的单纯形集合，几何实现不外是将空间“拼回去”；而对源于代数构造的单纯形集，几何实现则能用以构造分类空间。在单纯形集合上可以抽象地开展同伦论的研究。

另一方面，若取 A {\displaystyle {\mathcal {A}}} 为一阿贝尔范畴，对任一单纯形对象 A {\displaystyle A} 皆可定义一个链复形 N ( A ) {\displaystyle N(A)} 。此时单纯形对象与链复形的关系由以下定理阐明：

Dold-Kan对应定理（1957年）。函子 N {\displaystyle N} 给出范畴间的等价

透过这个对应，单纯形集合理论可助同调代数一臂之力，例如我们可借此定义更广义的导函子，或得到某类对象的典范分解。

非交换理论

源于同调论的古典同调代数只给出“可交换”的资讯。对于空间 X {\displaystyle X} 上的非交换群层 G {\displaystyle G} ，古典方法只能定义第一个上同调 H 1 ( X ; G ) {\displaystyle H^{1}(X;G)} ；这个集合分类了 X {\displaystyle X} 上的扭子。数学家们尝试定义高阶的非交换上同调，这方面的理论常牵涉到同伦理论、单纯形集合，或者高阶的范畴论（如叠论）。

同调代数与同伦代数

就模型范畴的观点，同调代数可被视为同伦理论的一支。这是Daniel Quillen将模型范畴理论称作同伦代数的原因 。

文献

Henri Cartan, Samuel Eilenberg, Homological algebra. Reprint of the 1956 original. Princeton Landmarks in Mathematics. Princeton University Press, Princeton, NJ, 1999. xvi+390 pp. ISBN 0-691-04991-2

Deligne, Pierre; ed. Séminaire de Géométrie Algébrique du Bois Marie - Cohomologie étale -（SGA 4½）（1977）, Lecture notes in mathematics 569), Berlin; New York: Springer-Verlag, iv+312.

Alexander Grothendieck, Sur quelques points d"algèbre homologique. Tôhoku Math. J.（2）9, 1957, 119--221

Gelfand, Sergei I.; Yuri Manin, Methods of homological algebra. Translated from Russian 1988 edition. Second edition. Springer Monographs in Mathematics. Springer-Verlag, Berlin, 2003. xx+372 pp. ISBN 3-540-43583-2

Weibel, Charles A., An introduction to homological algebra. Cambridge Studies in Advanced Mathematics, 38. Cambridge University Press, Cambridge, 1994. xiv+450 pp. ISBN 0-521-43500-5; 0-521-55987-1

Verdier, Jean-Louis, Des Catégories Dérivées des Catégories Abéliennes（1996）, Astérisque 239.

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。